第四章功和能 §4.1动能定理(Theorem of Kinetic Energy) 牛Ⅱ对空间的积分 1.功(work) (1)恒力、直线运动 F的功:A=F△cos0 =F△
§4.1 动能定理(Theorem of Kinetic Energy) ——牛Ⅱ对空间的积分 1.功 (work) (1) 恒力、直线运动 F 的功: A F r cos = F r F r = 第四章 功和能

2)变力、曲线运动 F(r) 元位移d所: dA=F(r).dr 整个路径L: A=F(r)d
(2) 变力、曲线运动 L dr F(r) 元位移 dr : dA F r dr = ( ) 整个路径L: = L A F r dr ( )

(3)常用计算式: A=JF+F,+F.d也 (4)合力的功: A=∑F) =∑f =∑4
(3)常用计算式: = + + L A Fx dx Fy dy Fz dz (4)合力的功: = L i i A F dr ( ) = i L i F dr = i Ai
例4-1AY 如图,质点沿圆周运动, 作用力F=k(xi+) (k为常量),则在从O到 A(0,2R)的过程中,力F X 作的功为 解:A=∫F,+F, =心kxd+d =2kR2
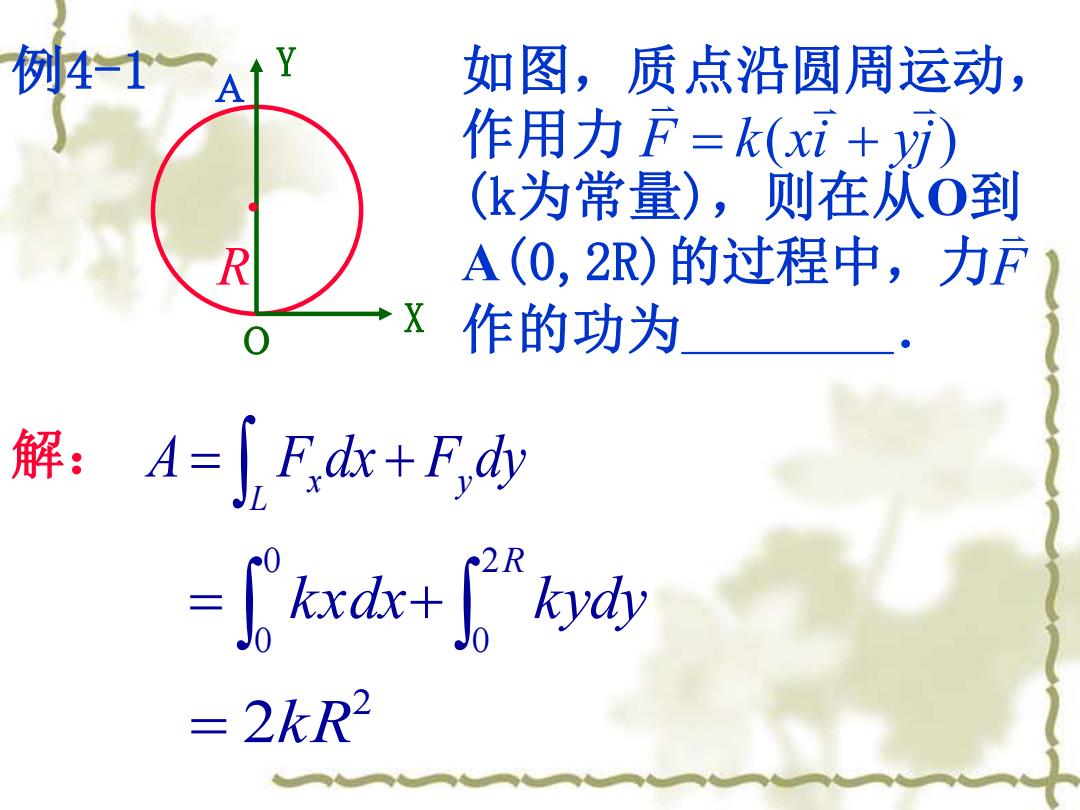
例4-1 X Y O R A 如图,质点沿圆周运动, 作用力 (k为常量),则在从O到 A(0,2R)的过程中,力 作的功为 . F k(xi yj) = + F 解: = + L x y A F dx F dy = + R kxdx kydy 2 0 0 0 2 = 2kR

思考1①其它算法? ②该力的功与路径形状是否有关?
[思考]①其它算法? ②该力的功与路径形状是否有关?

2.功率(power) 平均功率:p= △A △t 瞬时功率:P= dA =F dt [来历]: dA_Fdr=F.d=F.v dt dt dt
2.功率 (power) t A P 平均功率: = dt dA 瞬时功率: P = dt F dr dt dA [来历]: = F v = dt dr F = F v =
3.质点的动能定理 a F() Ab=3m-古mvd 合力的功质点动能的增量
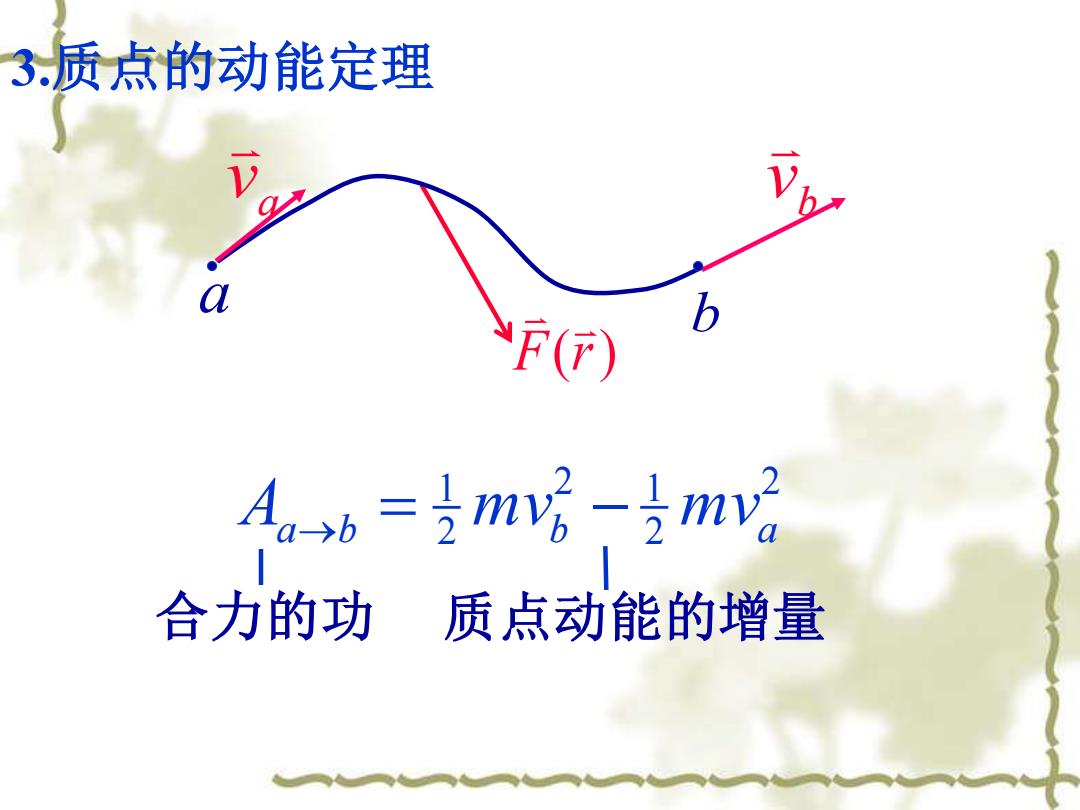
3.质点的动能定理 2 2 2 1 2 1 Aa→b = mvb − mva 合力的功 质点动能的增量 F(r) a b a v b v

d 证牛Ⅱ:F=m dt d →F.d=m 2df=mc.寸 .d(a.b)=da.b+a.db ∴.d.=d()=5d(w)=vdw →F.di=mvdw →F.d=wmvd →Ag→6=m-3mv
d a b da b a db ( ) = + ( ) 2 1 dv v d v v = → F dr = mvdv → = b a v v b L a F dr mvdv 2 2 2 1 2 1 → Aa→b = mvb − mva [证] dr dt dv F dr m → = dt dv F m 牛Ⅱ: = mdv v = ( ) 2 2 1 = d v = vdv

Note: 若质点速度接近光速,则动能定理 的叙述不变,但动能表达式改变!
Note: 若质点速度接近光速,则动能定理 的叙述不变,但动能表达式改变!

例4-2m=1kg的物体,在坐标原点处从静止出 发沿X轴运动,合力F=(3+2x)i(SI), 则在x=0~3m内,合力作功A= x=3m处,物体速率v= 解:(①A=Fd=3+2x)=18J (2)A=号mw2-0 >V= =6m/s m
例4-2 m=1kg的物体,在坐标原点处从静止出 发沿X轴运动,合力 (SI), 则在x=0~3m内,合力作功A= ; x=3m处,物体速率v= . F x i = (3+ 2 ) ⑴ = x A Fx dx 0 ⑵ 0 2 2 1 A = mv − m A v 2 → = 解: = + 3 0 (3 2x)dx =18 J = 6 m/s