
第六章 狭义相对论基础 (Special Relativity) Albert Einstein (1879-1955)
Albert Einstein (1879-1955) 第六章 狭义相对论基础 (Special Relativity)

科学业绩: 1、提出光的量子论 2、创建狭义相对论 3、创建广义相对论 1921年获诺贝尔物理学奖 虽镜理
科学业绩: 1、提出光的量子论 2、创建狭义相对论 3、创建广义相对论 1921年获诺贝尔物理学奖

本章:/伽利略相对性原理 狭义相对论基本原理 洛仑兹变换 相对论时空观 相对论速度变换 相对论动力学
本章: 伽利略相对性原理 狭义相对论基本原理 洛仑兹变换 相对论时空观 相对论速度变换 相对论动力学
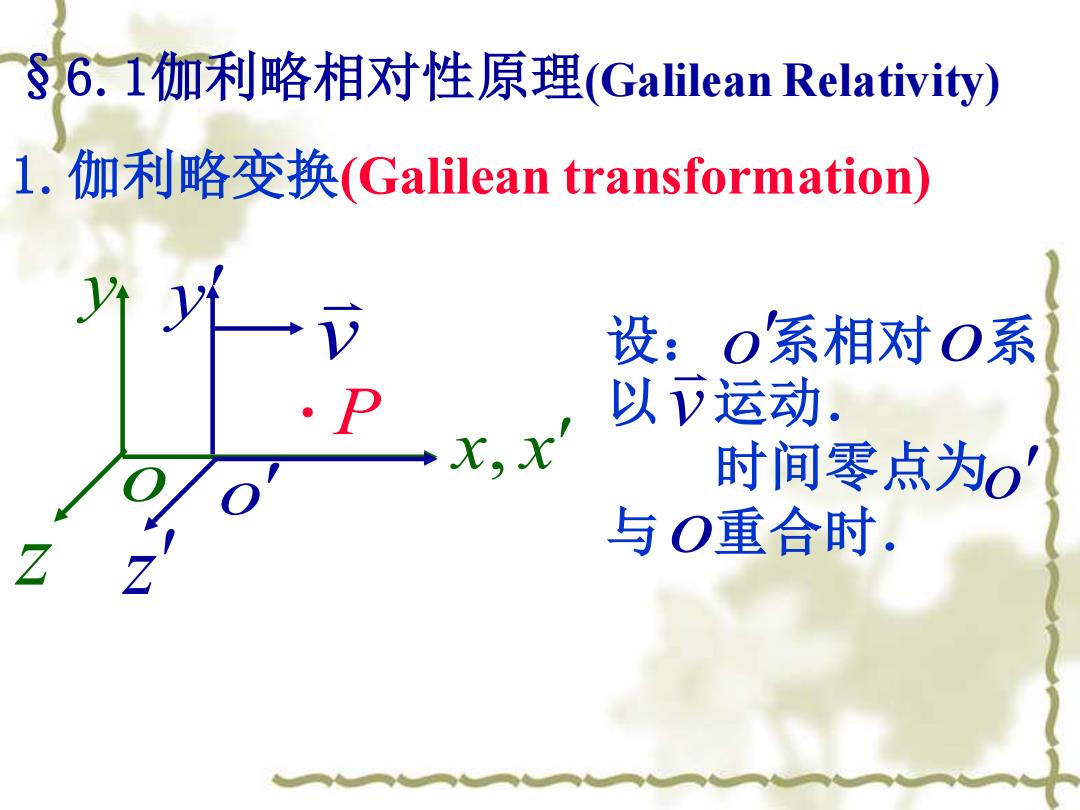
§6.I伽利略相对性原理(Galilean Relativity) l.伽利略变换(Galilean transformation) 设:o系相对O系 以)运动 x.x 时间零点为0 与O重合时
§6.1伽利略相对性原理(Galilean Relativity) 1.伽利略变换(Galilean transformation) 设: 系相对 系 以 运动. 时间零点为 与 重合时. o o v o o P x, x o y y v o z z

侧对于任一事件(event).P,有 == x-ut y 伽利略坐标变换 Note: 该变换意味着时间独立于空间,且时 间间隔及长度的测量结果与坐标系无 关 经典力学的时空观
则对于任一事件(event)P ,有 x = x −ut y = y z = z t = t ——伽利略坐标变换 该变换意味着时间独立于空间,且时 间间隔及长度的测量结果与坐标系无 关. ——经典力学的时空观 Note:

2.伽利略相对性原理 力学规律在所有惯性系中都有相同的 形式 e.g. 设0系中 F=ma 牛顿力学: F-F (力与参考系无关) m'm (质量与运动无关) 伽利略变换→ a'-a 于是在0'系中:F'=m'a
2.伽利略相对性原理 ——力学规律在所有惯性系中都有相同的 形式 牛顿力学: F F = (力与参考系无关) m = m (质量与运动无关) e.g. 设O系中 F ma = 于是在O系中: F = m a 伽利略变换→ a a =

Note: 另一种表述:牛顿力学规律在伽利 略变换下保持不变. 3.十九世纪末的困惑 (1)电磁场方程组不具有伽利略变换下的不 变性.(服从Lorentz?变换) (2)光速不服从伽利略速度变换 (Michelson-Morley实验)
另一种表述:牛顿力学规律在伽利 略变换下保持不变. Note: ⑵光速不服从伽利略速度变换. (Michelson-Morley实验) 3.十九世纪末的困惑 ⑴电磁场方程组不具有伽利略变换下的不 变性. (服从Lorentz变换)

S6.2狭义相对论基本原理(Fundamentals of Special Relativity) In1905,Einstein:《论动体的电动力学》 (1)物理规律对所有惯性系都是一样的,不存在 任何一个特殊的(例如“绝对静止”的)惯性 系. 相对性原理 (2)在任何惯性系中,光在真空中的速率都相等 光速不变原理 → 新的时空变换式
§6.2 狭义相对论基本原理(Fundamentals of Special Relativity) In 1905, Einstein:《论动体的电动力学》 ⑴物理规律对所有惯性系都是一样的,不存在 任何一个特殊的(例如“绝对静止”的)惯性 系. ——相对性原理 ⑵在任何惯性系中,光在真空中的速率都相等. ——光速不变原理 新的时空变换式
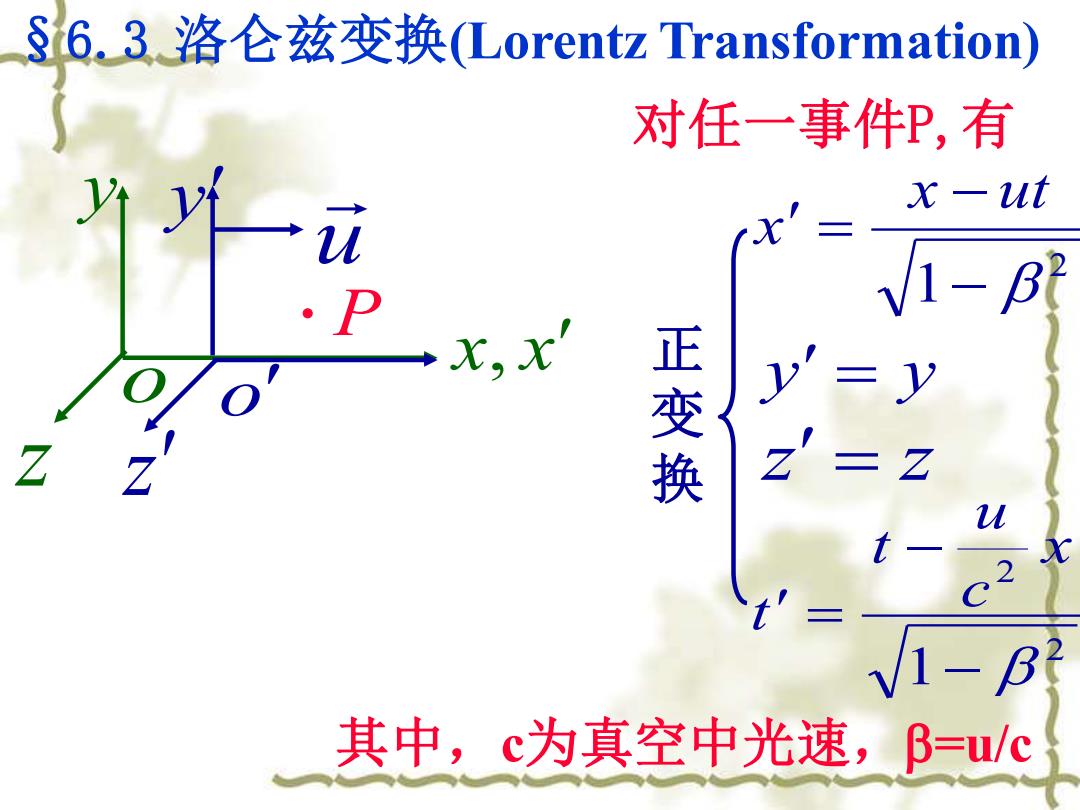
§6.3洛仑兹变换(Lorentz Transformation) 对任一事件P,有 x-ut P 1-B 正变换 z Z 1-B 其中,c为真空中光速,B=u/c
§6.3 洛仑兹变换(Lorentz Transformation) P x, x o y y u o z z 对任一事件P,有 2 1− − = x ut x y = y z = z 2 2 1− − = x c u t t 正 变 换 其中,c为真空中光速,=u/c
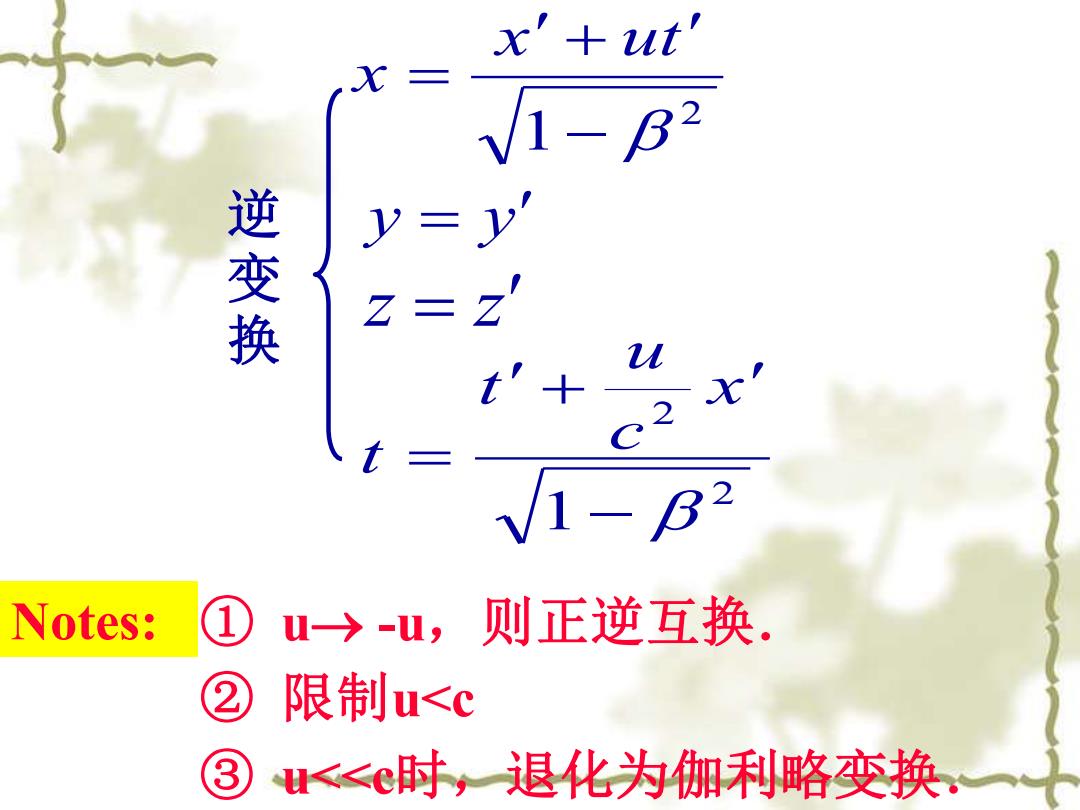
x'+t' 1-B2 逆变换 y B Notes: u〉-u, 则正逆互换. ② 限制u<c ③ u<C时,退化为伽利略变换
2 1− + = x ut x y = y z = z 2 2 1− + = x c u t t 逆 变 换 ① u→ -u,则正逆互换. ② 限制u<c Notes: ③ u<<c时,退化为伽利略变换.