
绪论(Introduction) 科学是一种方法。它教导人们:一些事物是怎样被了解的,什么事情是已知的,现在了 解到了什么程度(因为没有事情是绝对己知的),如何对待疑问和不确定性,证据服从什么法 则,如何去思考事物,做出判断,如何区别其伪和表面现象。 一、课程内容 力学、热学、电磁学、波动与光学 二、数学工具 矢量运算、微积分 三、散学要求 失量与标量 基本理论:三大守恒定律… 基本方法:微元分析… 力学(Mechanics) 质点运动学 质点力学 牛顿运动定律 运动的守恒定律 经典力学 (宏观低速) 一刚体的定轴转动 力学 狭义相对论 (宏观高速) 第一章质点运动学 (Kinematics of Particles) §l.l质点与参考系(Material Particles and Reference Frames) 1.质点(理想模型) object with no size(大小形状可以忽略的,具有质量的点) 适用情形:物体尺寸<《运动范围 2.参考系 -coordinate system in a reference object (为描述物体运动而选定的标准物体)
绪 论(Introduction) 科学是一种方法。它教导人们:一些事物是怎样被了解的,什么事情是已知的,现在了 解到了什么程度(因为没有事情是绝对已知的),如何对待疑问和不确定性,证据服从什么法 则,如何去思考事物,做出判断,如何区别真伪和表面现象。 ——R. P. Feynman 一、课程内容 力学、热学、电磁学、波动与光学 二、数学工具 矢量运算、微积分 三、教学要求 基本概念:矢量与标量…… 基本理论:三大守恒定律…… 基本方法:微元分析…… 力学(Mechanics) 第一章 质点运动学 (Kinematics of Particles) §1.1质点与参考系( Material Particles and Reference Frames ) 1.质点(理想模型) ——object with no size(大小形状可以忽略的,具有质量的点) 适用情形:物体尺寸 << 运动范围 2.参考系 ——coordinate system in a reference object (为描述物体运动而选定的标准物体) ——刚体的定轴转动 力学 经典力学 (宏观低速) 狭义相对论 (宏观高速) 刚体 力学 质点力学 质点运动学 牛顿运动定律 运动的守恒定律
a参考系的引入是由于运动相对性的需要。 b参考系的选择是任意的, 对不同的参考系质点运动形式不同。 ©通常我们选地面或固定于地面的物体为参考系 §1.2运动的描述(Description of Motion) 1.位矢(position vector) P(x.v.Z) F0=x()i+0j+(0k 一运动方程or运动函数 cg抛体运动: X F)=oi+(o,1-g2 2.位移(displacement) △F=Fu+△)-Ft) 一t至t+△t内的位移 P1△S cg.设F0=i+万+12派(S) △F P2 则在0至1s内的位移 F0t+△) 少=0)-F(0)=j+Km 0 X Notes:①l△≠AS 但d=dS 产(t) △ ②l△≠y F(t+△t) 但d≠d 3.速度(velocity) 平均速度:币= △t Average velocity 瞬时速率:= △示d行 Instantaneous velocity: Ns0平约车,一名-同
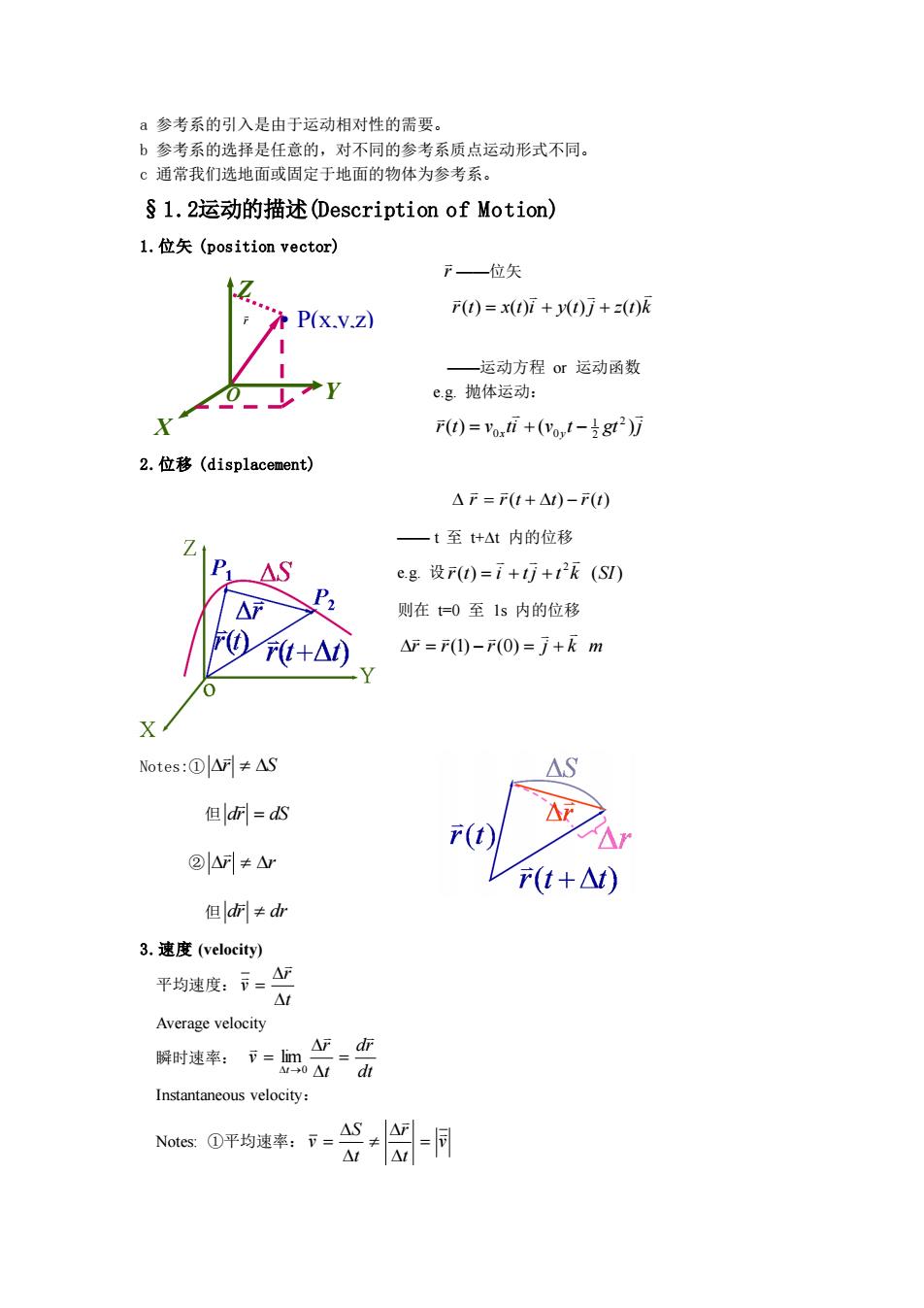
a 参考系的引入是由于运动相对性的需要。 b 参考系的选择是任意的,对不同的参考系质点运动形式不同。 c 通常我们选地面或固定于地面的物体为参考系。 §1.2运动的描述(Description of Motion) 1.位矢 (position vector) r ——位矢 r t x t i y t j z t k ( ) = ( ) + ( ) + ( ) ——运动方程 or 运动函数 e.g. 抛体运动: r t v ti v t gt j x y ( ) ( ) 2 2 1 = 0 + 0 − 2.位移 (displacement) r r(t t) r(t) = + − —— t 至 t+t 内的位移 e.g. 设 ( ) ( ) 2 r t i t j t k SI = + + 则在 t=0 至 1s 内的位移 r r r j k m = (1) − (0) = + Notes:① r S 但 dr = dS ② r r 但 dr dr 3.速度 (velocity) 平均速度: t r v = Average velocity 瞬时速率: dt dr t r v t = = →0 lim Instantaneous velocity: Notes: ①平均速率: v t r t S v = = O X Z Y r • P(x,y,z)

车空宫-问 curvilinear motion,the velocity vector is tangential to the curve 一些速度值(m/s) 直空中光速 -3.0×10 太阳在银河系中的运动 -3.0×10 地球的公转 -3.0x10 人造地球卫星 7.9x10 现代歼击机 -9×10 空气中声速 -3.3×102 猎豹 2.8×10 10 1 4.加速度(acceleration). 平均加速度:石=△ e.g.设F(t)=i+j+2k(S) =7+2 则0=dF」 a0=4=2m1s d -些加速度值(m/s2) 子弹在枪膛中的加速度 5x10 车祝毅间的加速府 -1×10 致人晕眩的加速度 -7×10 地球表面的重力加速度 9.8 月球表面的重力加速度 -1.7 地球自转引起赤道上的加速度 -3.4×10 地球公转的加速度 6x103 太阳绕银河系中心转动的加速度 -3×100 5,两类向愿 (①)(球导)F)→下)→ā0 (2)(积分)ā0)0→0)0→0) [例1-1质点的运动方程为=3+5t+6t2-t(SI),则①t=0时,速度 :②加速度为 零时,速度一 解:①-dr/d=5+12t-3t2→w=5mls ②ad/d=12-6t=0→t=2s→1=17ms
瞬时速率: v dt dr dt dS v = = = ②In curvilinear motion, the velocity vector is tangential to the curve. 一些速度值(m/s) 真空中光速 ∼3.0108 太阳在银河系中的运动 ∼3.0105 地球的公转 ∼3.0104 人造地球卫星 ∼7.9103 现代歼击机 ∼9 102 空气中声速 ∼3.3102 猎豹 ∼2.8 10 载流导线中自由电子的漂移 ∼10–4 大陆板块运动 ∼10–9 4.加速度 (acceleration) 平均加速度: t v a = 瞬时加速度: 2 2 0 lim dt d r dt dv t v a t = = = → e.g. 设 ( ) ( ) 2 r t i t j t k SI = + + 则 ( ) j 2 tk (SI) dt d r v t = = + 2 ( ) 2k m/s dt d v a t = = 一些加速度值(m/s2) 子弹在枪膛中的加速度 ∼5105 车祸瞬间的加速度 ∼1103 致人晕眩的加速度 ∼710 地球表面的重力加速度 ∼9.8 月球表面的重力加速度 ∼1.7 地球自转引起赤道上的加速度 ∼3.410–2 地球公转的加速度 ∼610–3 太阳绕银河系中心转动的加速度 ∼310–10 5.两类问题 (1) (求导) r(t) v(t) a(t) → → (2) (积分) ( ) ( ) ( ) (0) (0) a t v t r t v r ⎯⎯→ ⎯⎯→ [例1-1] 质点的运动方程为 x=3+5t+6t2–t 3 (SI),则①t=0时,速度v0= ; ②加速度为 零时,速度v= . 解:①v=dx/dt= 5+12t–3t2→ v0=5 m/s ②a=dv/dt=12–6t= 0→ t=2s → v=17 m/s

「思考]加速度为零时,速度值是否极大? y=4+2(S),则①位置矢量表达式:②速度的表达式 解:①=3i+(42+2)j @f-年-i+12r 国y=4x(y+2=4 27*3 [思考加速度为零时,速度值是多少 [例1-3】质点沿x轴运动:t=0时,质点位于原点,速度为零,加速度为a=3+4(SI),则① 速度的表达式:②位移表达式。 鼎①a-密安套会+4=小-B+4h=5x+2 di= v3r+2r∫a dx 积分 可得出结果 [例14]求:在任意位置x处,船的速度和加速度 7 设在任意位置x处,绳长为 则有x=VP-所 且dl1d=-o 于是= 密2n贵白 21 [思考1船做何种运动?(变加速直线运动) 1-5】某物体的运动规律为d/t-kt(k为常数),t=0时,=,求与t的函数关系。 解 h1d=-→-=j→=1+ [思考]若dWd=a(常量),结果?(=w+a心) 2+ §1.3曲线运动(Curvilinear Motion) 特点:()下沿曲线切向 (2)a=a.+a d,-tangential a。-normal
[思考] 加速度为零时,速度值是否极大? [例1-2] 质点的运动方程为 x=3t;y=4t3+2 (SI),则①位置矢量表达式; ②速度的表达式; ③加速度表达式;④运动轨道方程。 解:① r ti t j 3 (4 2) 3 = + + ② i t j dt dr v 3 ˆ 12 ˆ 2 = = + ③ tj dt dv a = = 24 ˆ ④ 2 27 4 ) 2 3 4 ( 3 3 = + = + x x y [思考] 加速度为零时,速度值是多少? [例1-3] 质点沿x轴运动;t=0时,质点位于原点,速度为零,加速度为a=3+4x (SI),则① 速度的表达式; ②位移表达式。 解:① 2 3 4x vdv (3 4x)dx v 3x 2x dx dv v dt dx dx dv dt dv a = = = + = + = + ② = + = dt x x dx dt dx v 2 3 2 积分 可得出结果 [例1-4] 求:在任意位置x处,船的速度和加速度 设在任意位置x处,绳长为l 则有 2 2 x = l − h 且 0 dl / dt = −v 于是 [思考]船做何种运动?(变加速直线运动) [例1-5] 某物体的运动规律为dv/dt=–kv 2 t (k为常数), t=0时, v=v0,求v与t的函数关系. 解: [思考] 若dv/dt=a(常量),结果?(v=v0+at) §1.3曲线运动(Curvilinear Motion) 特点:⑴ v 沿曲线切向 ⑵ a at an = + t a —tangential n a —normal dt dx v = dt dl l h l − = 2 2 2 2 2 0 1 ( ) x h = −v + dt dv a = dt dx v x h x h x h + − = − 2 0 2 1 ( ) 2( )( 2 ) 3 2 0 2 x h v = − dv dt kv t 2 / = − → − = v t v ktdt v dv 0 2 0 ) 1 2 1/( 0 2 v kt → v = +

Notes①a,=a,g切向单位矢量(与速度方向一致) 一速度大小对时间的变化率 ②ān=anE。法向单位矢量(指向曲线凹侧) s2 一反映速度方向变化的快慢 P一质点所在处曲线的曲率半径 Attention:仅在曲线的拐点(inflexion)处,才有aa=O 1.圆周运动(circular motion) 一线位移孤弧长) v=d本/d山—线速度 a,=/—切向加速度 an=21p—法向加速度 角量:0一角位(rad o=deldt- 角速度(rads) a=d201d2一角加速度(rads3) 线量与角量的关系:S=R0 v=Ro a,=Ra a=Ro 匀变速率运动: a匀速直线运动v=%+a,1S=o1+a,12v2-哈=2a,S b匀速圆周运动0=0。+a10=l+at2o2-6=2a0
Notes: ① t t t a a e = 切向单位矢量(与速度方向一致) dt dv at = ——速度大小对时间的变化率 ② n n n a a e = 法向单位矢量(指向曲线凹侧) 2 v an = ——反映速度方向变化的快慢 —质点所在处曲线的曲率半径 Attention: 仅在曲线的拐点(inflexion)处,才有an=0 . 1.圆周运动(circular motion) 特点:R 线量:S ——线位移(弧长) v = ds/ dt ——线速度 a dv dt t = / ——切向加速度 / 2 a v n = ——法向加速度 角量: ——角位移(rad) = d / dt ——角速度(rad/s) 2 2 = d / dt ——角加速度(rad/s2 ) 线量与角量的关系: S = R v = R at = R 2 an = R 匀变速率运动: a 匀速直线运动 v v a t = 0 + t 2 2 1 0 S v t a t = + t v v 2at S 2 0 2 − = b 匀速圆周运动 = + t 0 2 2 1 0 = t + t 2 2 0 2 − =

[例1-6]质点沿半径为0.1m的圆周运动,其角 位骂25S)别子时, 25.6m/s1 an= z0h+→ 解:思路00→u 0 a=Ra [思路二])→ )++ a(0)→a [思考]何种圆周运动? 2.抛体运动(projectile motion) 加速度: 速度: H [Vx=Vox ① L 1Vy=V'oy-8t② 运动方程: [x Voxt ③ ly=ovt-gt2④ ①~④→ H,L,轨迹方程等
[例1-6]质点沿半径为 0.1m的圆周运动,其角 位 置 =2+4t2 (SI) , 则 t=2s 时 , an = , at= . 解:[思路一] (t) (t) at=R [思路二] (t) S(t) at(t) at v(t) v an=v2 /R 25.6 m/s2 0.8 m/s2 (t) an=R 2 [思考] 何种圆周运动? ⒉抛体运动(projectile motion) 加速度: a g x y o 0 v H L 速度: x x v v = 0 ① v v gt y = 0 y − ② 运动方程: x v t = 0x ③ 2 2 1 y v0 t gt = y − ④ ①~④ H , L , 轨迹方程等

[例1-7]物体作斜抛运动如图,测得在轨道A 点处速度的大小为,其方向与水平 方向夹角成30°.则物体在A点的切 向加速度=,轨道的曲率半径 p= 解:(①)
解:⑴ at = −g cos60 物体作斜抛运动如图,测得在轨道A 点处速度的大小为v,其方向与水平 方向夹角成30. 则物体在A点的切 向加速度at= ,轨道的曲率半径 = . g v A 30 [例1-7] 2 g = −

5 a月 [思考]轨道最高点处的曲率半径? a.-vle 公 式 的应用?
2 v an = an = g cos30 ⑵ n a v 2 = [思考] 轨道最高点处的曲率半径? g 2 3 = g v 3 2 3 2 = 公 式 的应用? 2 a v n =

§1.4相对运动Relative Motion) —运动描述的相对性 设0系相对于0系做平移运动 在0系中观察:〔0'点位矢为F。 0'系速度为下。 O'系加速度为a。 设质点在0系中有:r,下,d 在0'系中有:F',',a 则 -a+ Note:以上关系仅当下。<C(光速)时成
§1.4 相对运动(Relative Motion) 设O系相对于O 系做平移运动 O´ r O or r 在O 系中观察: o r O点位矢为 o v O系速度为 O系加速度为 o a ——运动描述的相对性 r v a 在O , , 系中有: r v a 设质点在O系中有: , , 则 o r r r + = o v v + v = a a + ao = 以上关系仅当| |<< C (光速)时成 立. o v Note:

Chap.1 SUMMARY 1.运动的描述 7, 两类问题: ()产(t)→(t)→(t)(求导) 2a090)9r0) (积分) 2.圆周运动:,S=R0 y=ds/dt Ro a=dv/dt=Ra an=v2/R=Ro2 匀变速率圆周运动: =+ %+
Chap.1 SUMMARY 1. 运动的描述 两类问题: (1) r(t) v(t) a(t) → → (求导) (2) a(t) v(t) r(t) (积分) → → v(0) r(0) r t r v a ( ), , , —— 2. 圆周运动:S = R v = ds/dt = R at= dv/dt = R an= v 2 /R = R 2 匀变速率圆周运动: v v a t = 0 + t 2 2 1 0 S v t a t = + t v v 2at S 2 0 2 − = = + t 0 2 2 1 0 = t + t 2 2 0 2 − =