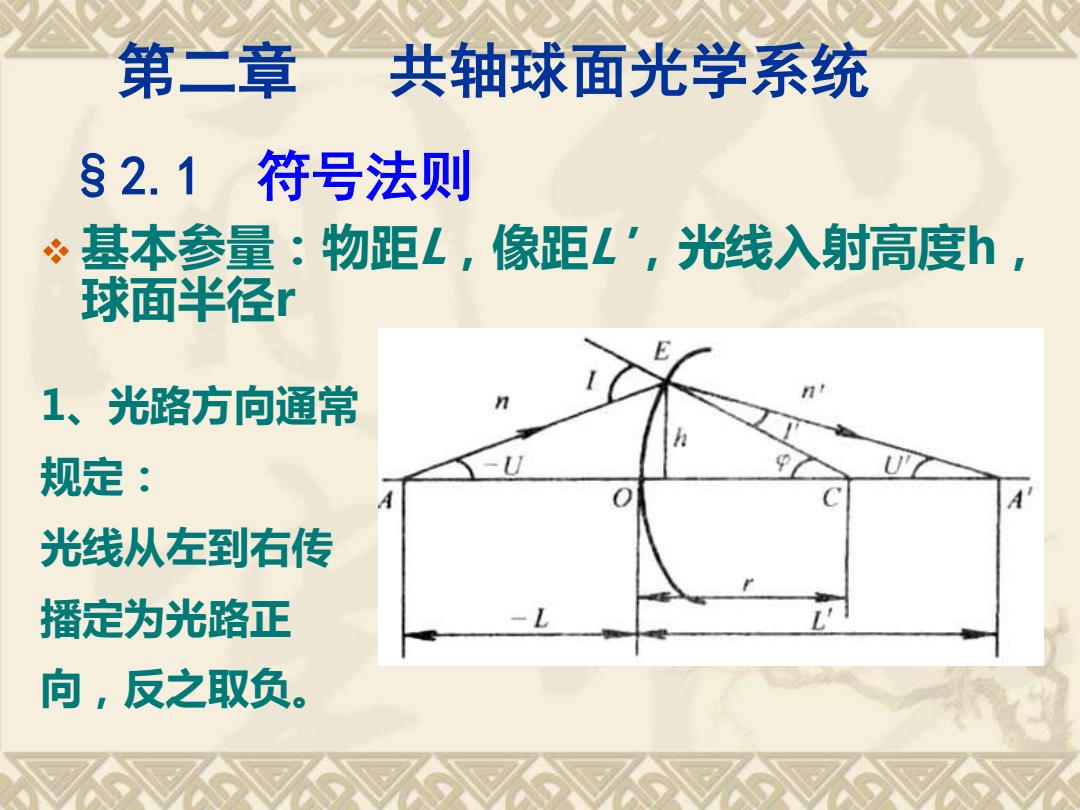
第二章 共轴球面光学系统 §2.1符号法则 基本参量:物距L,像距L',光线入射高度h, 球面半径r 1、光路方向通常 规定: 光线从左到右传 播定为光路正 向,反之取负
第二章 共轴球面光学系统 §2.1 符号法则 1、光路方向通常 规定: 光线从左到右传 播定为光路正 向,反之取负。 ❖ 基本参量:物距L,像距L',光线入射高度h, 球面半径r
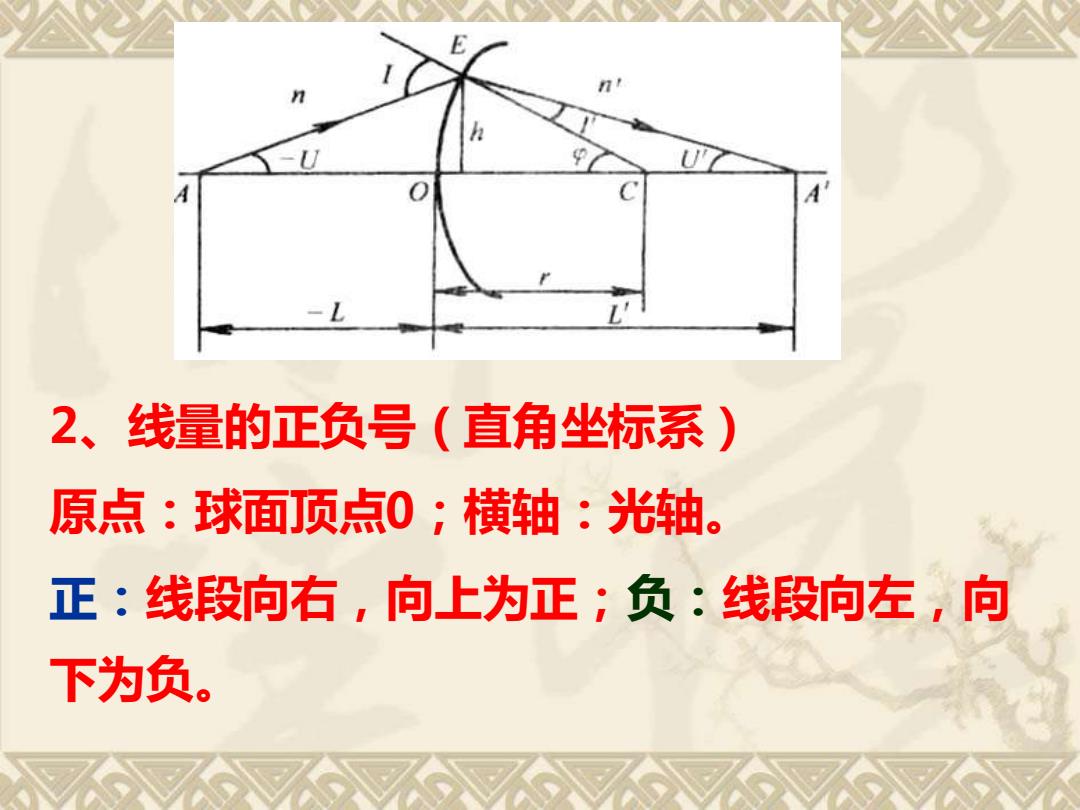
2、线量的正负号(直角坐标系) 原点:球面顶点0;横轴:光轴。 正:线段向右,向上为正;负:线段向左,向 下为负
2、线量的正负号(直角坐标系) 原点:球面顶点0;横轴:光轴。 正:线段向右,向上为正;负:线段向左,向 下为负
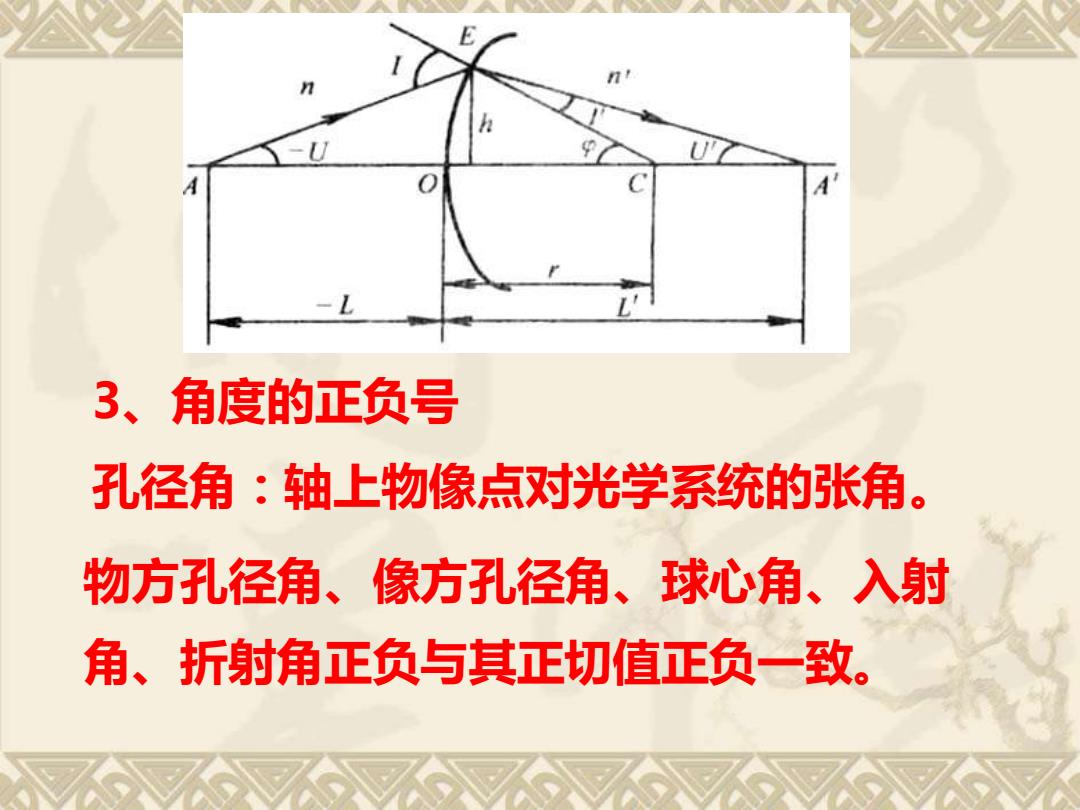
3、角度的正负号 孔径角:轴上物像点对光学系统的张角。 物方孔径角、像方孔径角、球心角、入射 角、折射角正负与其正切值正负一致
3、角度的正负号 孔径角:轴上物像点对光学系统的张角。 物方孔径角、像方孔径角、球心角、入射 角、折射角正负与其正切值正负一致

结论:L,U为负;h、L',U’、I、I'、 φ为正。 符号规则的意义: 物象的虚实和正倒。 1、负物距对应实物:正物距对应虚物。 2、正像距对应实像;负像距对应虚象。 3、像高和物高符号相反则成倒立像,反之 成正立像
符号规则的意义: 物象的虚实和正倒。 1、负物距对应实物;正物距对应虚物。 2、正像距对应实像;负像距对应虚象。 3、像高和物高符号相反则成倒立像,反之 成正立像。 结论:L、U为负;h、 L’ 、 U’、I、I’ 、 为正
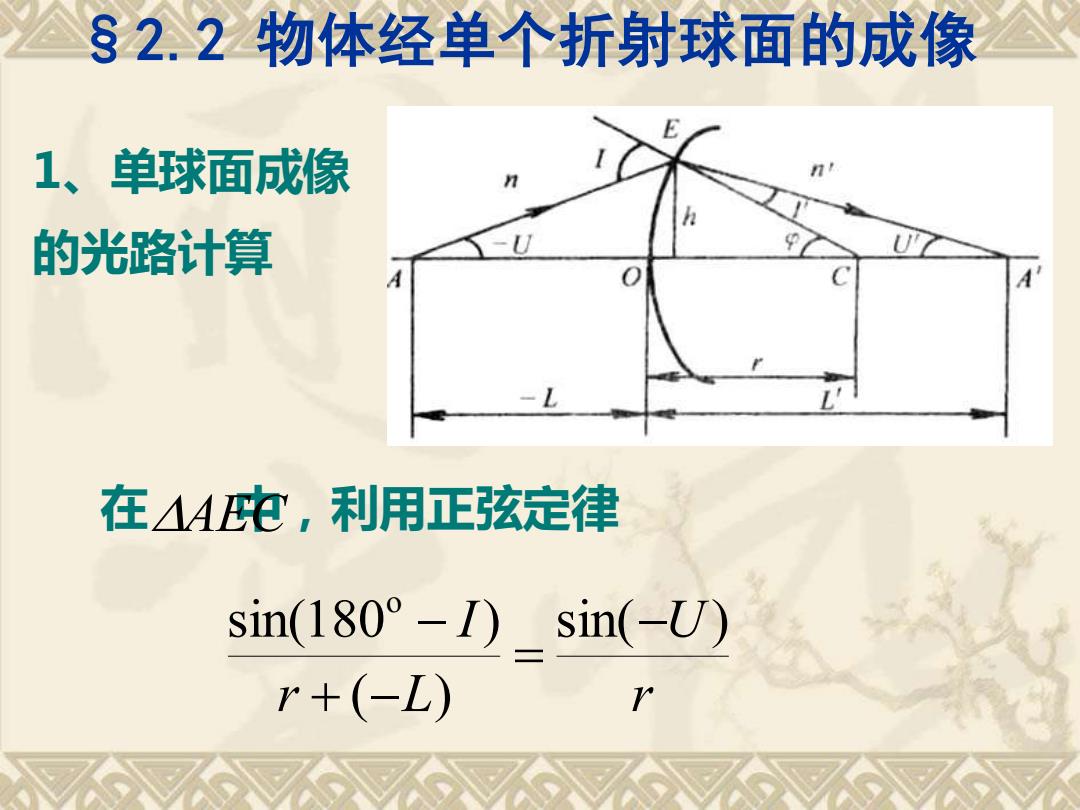
§2.2物体经单个折射球面的成像 1、单球面成像 的光路计算 在人4电,利用正弦定律 sin(180°-)sin(-U) r+(-L)
§2.2 物体经单个折射球面的成像 1、单球面成像 的光路计算 在 AEC 中,利用正弦定律 r U r L I sin( ) ( ) sin(180 ) o − = + − −

L-K sin/= sinU (2-1) 在E点应用折射定律得: sinI'=”sinl (2-2) n 由图中可知:p=+U'=I+U 像方孔径角 U=U+I-I (2-3)
在E点应用折射定律得: 由图中可知: = I'+U' = I +U sin sin L r I U r − = (2-1) I n n I sin ' sin ' = (2-2) U' =U + I − I' 像方孔径角 (2-3)

在△A'跑 sin I' sin U' L'-r 得到像方截距: L'= sin I' r+r (2-4) sin U
在 A'EC 中 r U L r I sin ' ' sin ' = − r r U I L + = sin sin ' 得到像方截距: (2-4)
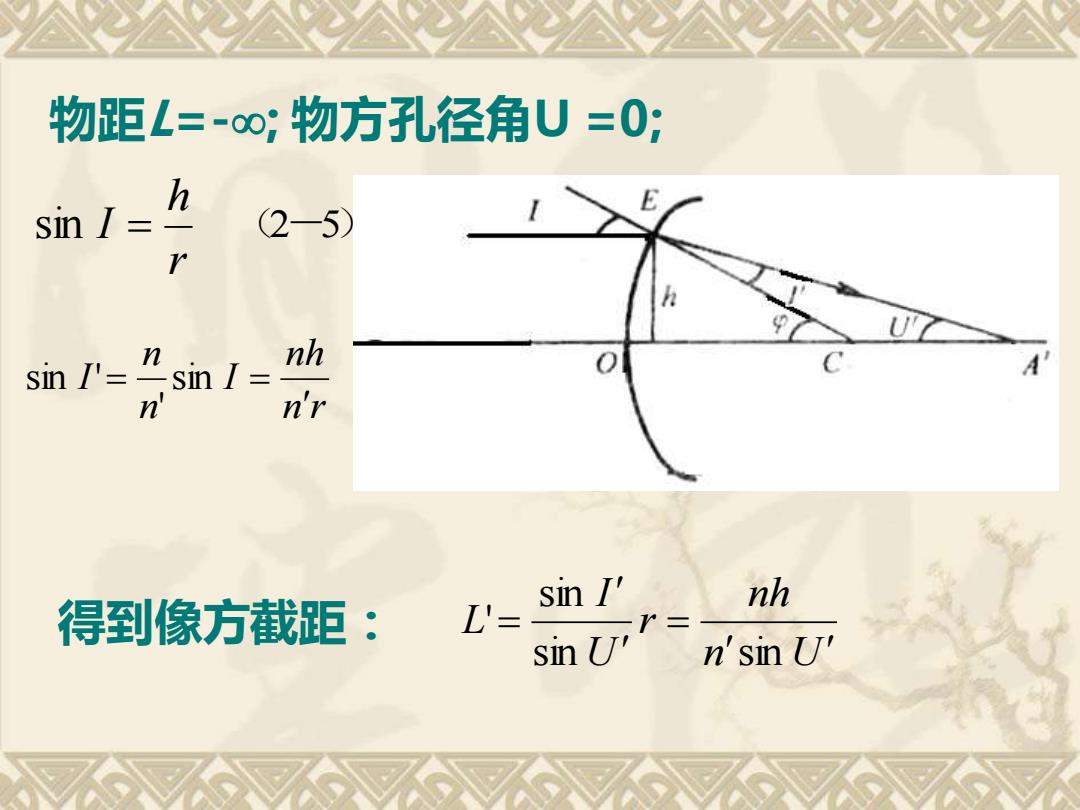
物距L=-oo;物方孔径角U=0; h (2-5) r sn'=sn1= n nh n n'r 得到像方截距: l= sin I' nh sin U' n'sin U
物距L=-; 物方孔径角U =0; r h sin I = (2-5) n r nh I n n I = sin = ' sin ' n U nh r U I L = = sin sin sin 得到像方截距:

2.近轴光路计算公式 非常小,这个区域称之为近轴区,则 I也非常小。 Snx≈x尤为孤度值 用弧度值代替正弦值
2. 近轴光路计算公式 I I' U ' U 非常小,这个区域称之为近轴区,则 也非常小。 sin x x x 为弧度值 用弧度值代替正弦值

u ~sinU u'~sinU' i~sin I i'~sin I' I-L '≈L (2-1)~(2-4)式变为: i=(l-r)u/r i'=n-iln' (2—6~9) u'=uti-i l'=r+r.i'/u
u ~ sinU i ~ sin I l ~ L l' ~ L' i ~ sin I u' ~ sinU' (2-1)~(2-4)式变为: i = (l − r)u /r i = ni/ n u = u + i −i l = r + ri/u (2-6 ~ 9)