
Source of magnetic field
Source of magnetic field

Agenda today 1.Biot-Savart-Laplace Law 2.the application of Biot-Savart-Laplace Law 3.Ampere's Law 4.The magnetic field of toroid and solenoid
Agenda today 1. Biot-Savart-Laplace Law 2. the application of Biot-Savart-Laplace Law 3. Ampere’s Law 4. The magnetic field of toroid and solenoid
The source of magnetic field
The source of magnetic field N S I
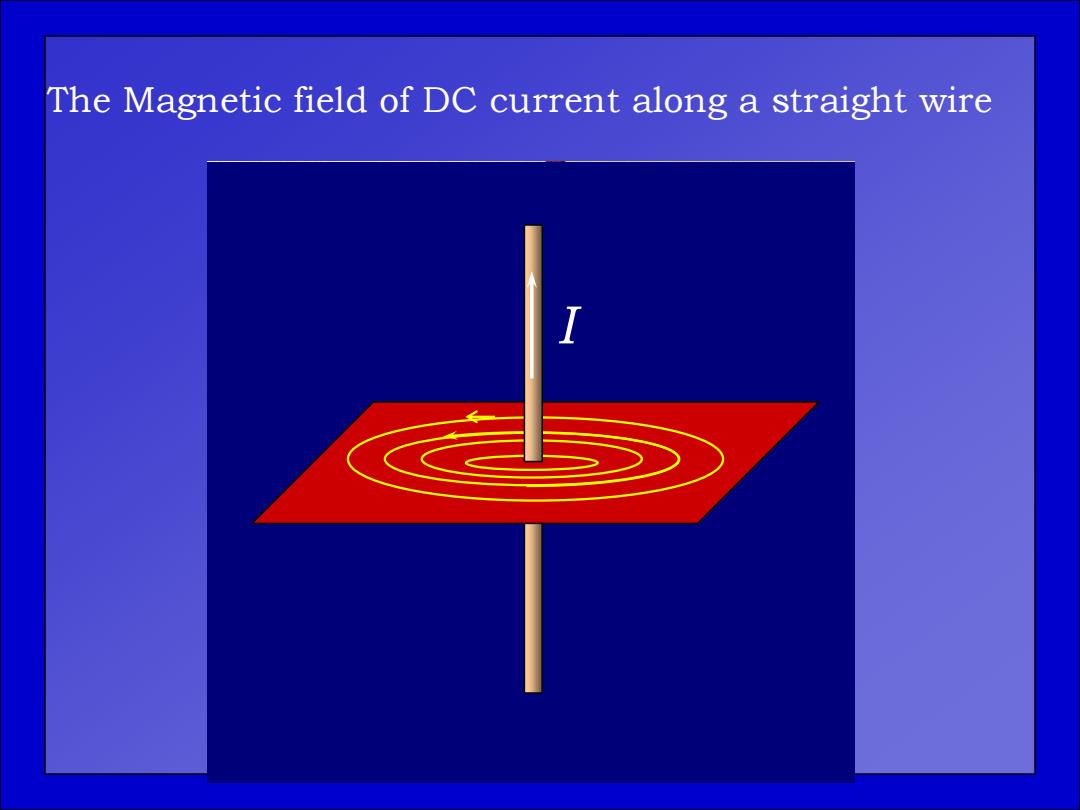
The Magnetic field of DC current along a straight wire
The Magnetic field of DC current along a straight wire I
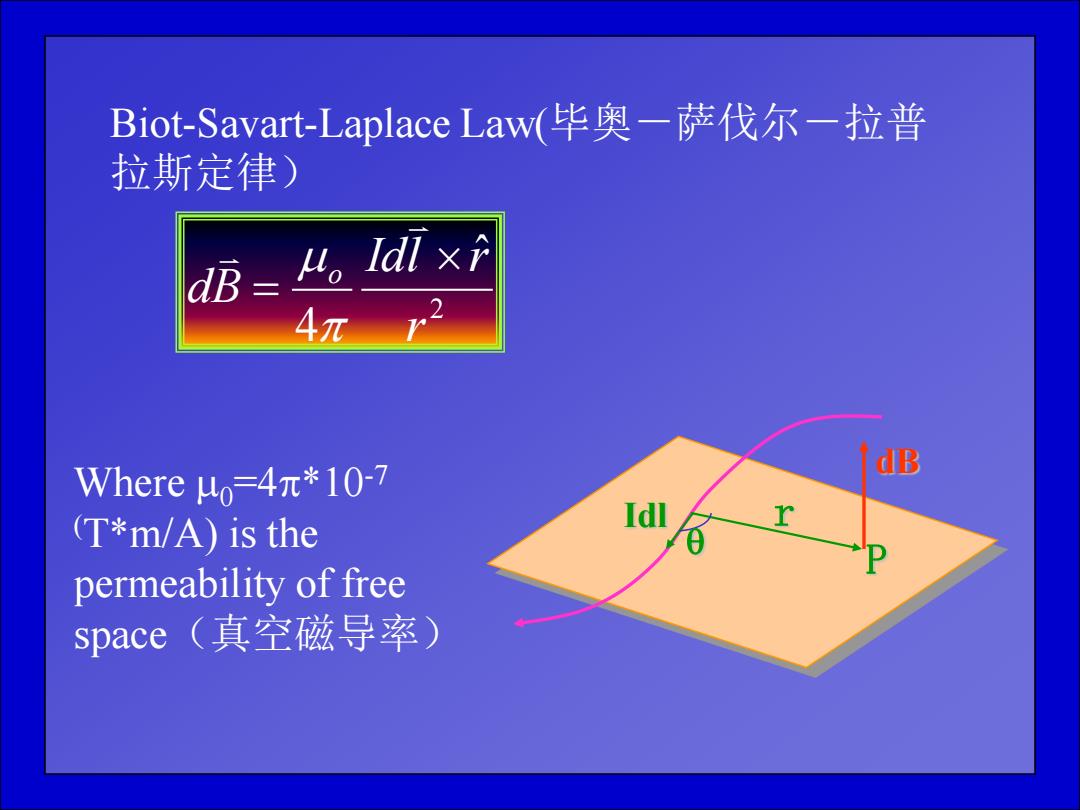
Biot-Savart-.Laplace Law(毕奥一萨伐尔一拉普 拉斯定律) dB 4,ldlx分 Where Ho=4π*10-7 dB (T*m/A)is the permeability of free space(真空磁导率)
Biot-Savart-Laplace Law(毕奥-萨伐尔-拉普 拉斯定律) 2 ˆ 4 r Idl r dB o P dB Idl r Where 0=4*10-7 (T*m/A) is the permeability of free space(真空磁导率)
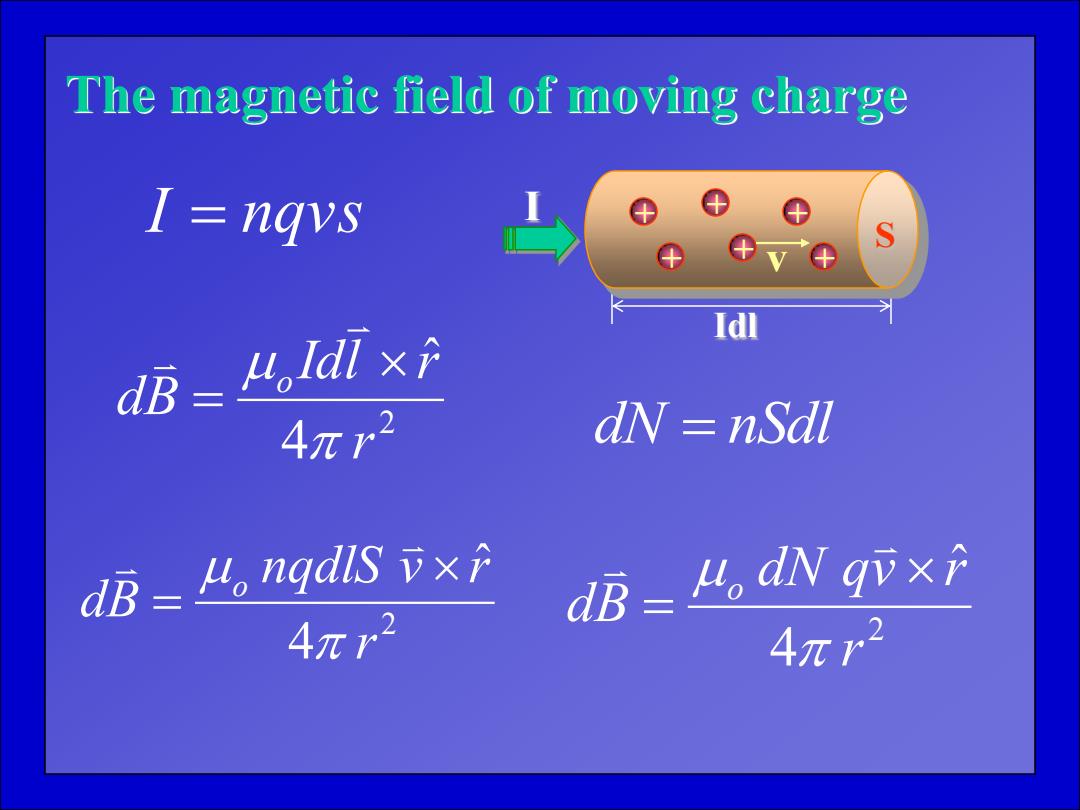
The magnetic field of moving charge I=ngvs ⊕ ⊕v④ Idl dB=。ldlx Anr2 dN nSdl dB=4。ngdls vxp dB=4。an qvx分 4r2 4π2
The magnetic field of moving charge Idl + + + + + v + I S 2 4 ˆ r Idl r dB o 2 4 ˆ r nqdlS v r dB o 2 4 ˆ r dN qv r dB o I nqvs dN nSdl

B= 4。q× 4π The magnetic force and conservation of momentum ql 2 B1
2 ˆ 4 r qv r B o The magnetic force and conservation of momentum B1 + v q1 + F12
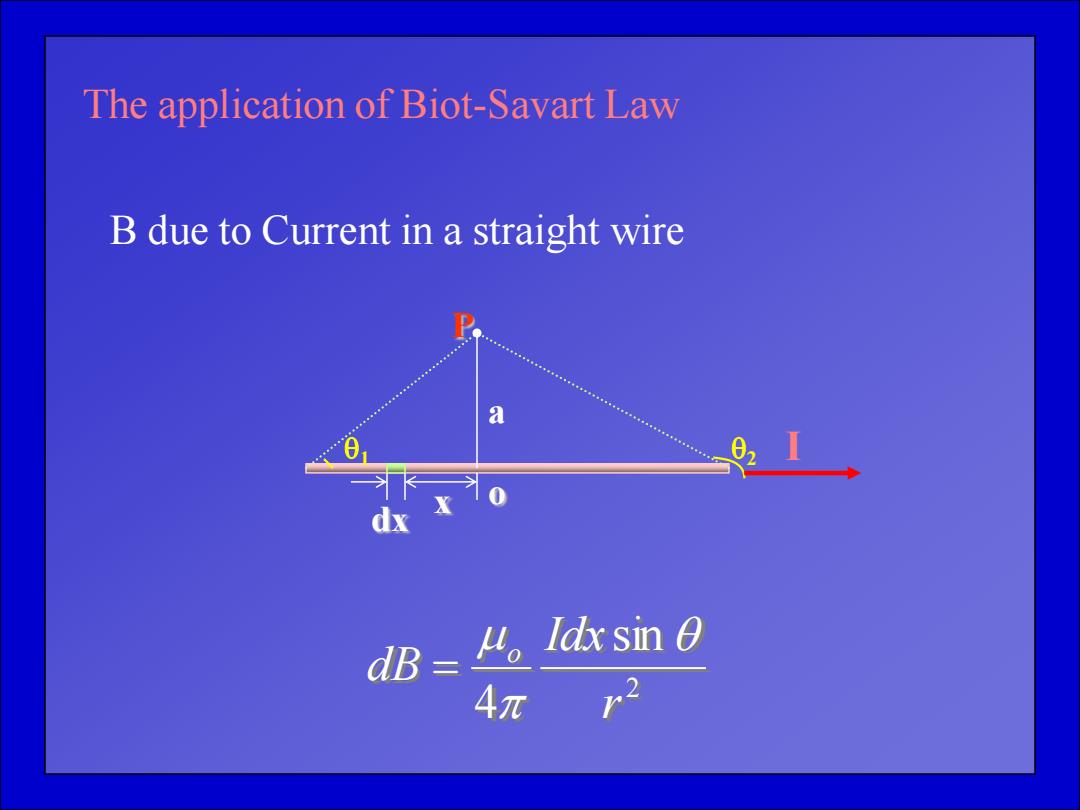
The application of Biot-Savart Law B due to Current in a straight wire a dx dB=to ldx sin 0 3 4π
The application of Biot-Savart Law B due to Current in a straight wire 2 o 1 P a dx x I 2 sin 4 r Idx dB o

x=-actge d众= ad0 sin20 a r= sin 0 8== sin 0do a2 sin 0de
x a ctg 2 sin a d dx sin a r d a I a B dB o sin sin 4 sin 2 2 2 2 1 sin 4 d a I B o

B=ML (cose,-cose,) 4π If the wire is infinite long 01=0,02=元 B= 2πa The definition of the Ampere If two very long parallel wires one meter apart carry equal current in each is defined to be one ampere if the force per unit length on each wire is 2*10-7N/m
1 2 cos cos 4 a I B o 1= 0 , 2 = If the wire is infinite long a I B o 2 The definition of the Ampere If two very long parallel wires one meter apart carry equal current in each is defined to be one ampere if the force per unit length on each wire is 2*10-7 N/m