
The Kinetic Theory of Gas
The Kinetic Theory of Gas

Agenda Today ·Ideal gas Pressure and temperature micro interpretation) Internal energy of idea gas Distribution law of molecular speed for ideal gas mean free path
Agenda Today • Ideal gas • Pressure and temperature ( micro interpretation) • Internal energy of idea gas • Distribution law of molecular speed for ideal gas • mean free path

The ideal--gas law(理想气体状态方程) m PV=RT M M:molar mass(摩尔质量) R:universal gas constant(普适气体常数) R=8.31J/mol'k
The ideal-gas law(理想气体状态方程) RT M m PV M: molar mass(摩尔质量) R: universal gas constant(普适气体常数) R=8.31J/molk
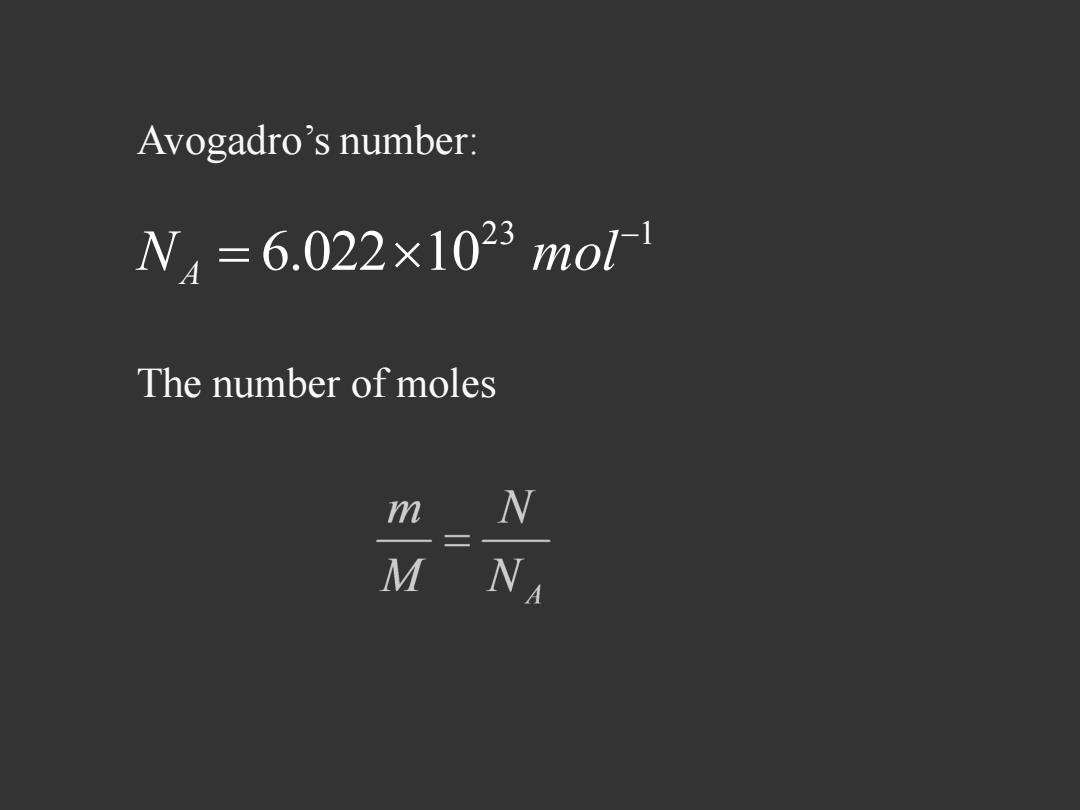
Avogadro's number: N4=6.022×1023mo1 The number of moles N M NA
23 1 6.022 10 N mol A Avogadro’s number: The number of moles
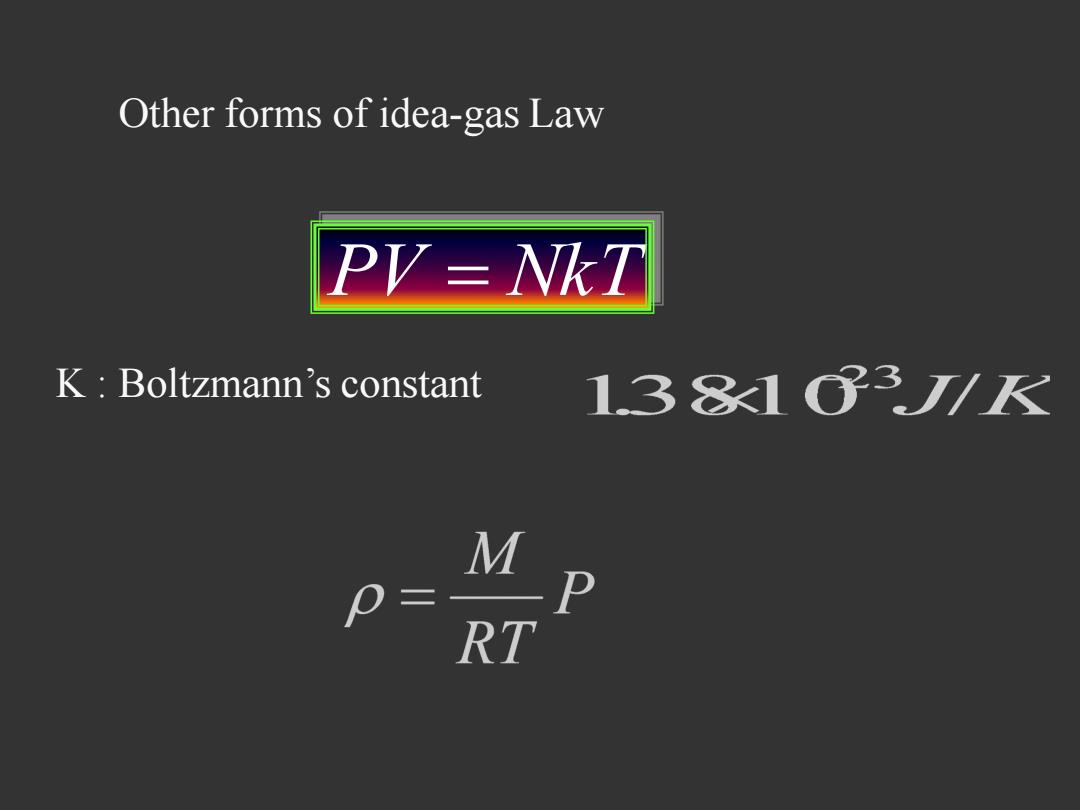
Other forms of idea-gas Law PV-NKT K:Boltzmann's constant 13813/K M 0= RT
PV NkT K : Boltzmann’s constant Other forms of idea-gas Law

The molecular interpretation of temperature: the kinetic theory of gases 1 the gas consists of a large number of molecules that make elastic collisions with each other and with the walls of the container 2 the molecules are separated,on the average, by the distances that are very large compared with their diameters
The molecular interpretation of temperature: the kinetic theory of gases 1 the gas consists of a large number of molecules that make elastic collisions with each other and with the walls of the container 2 the molecules are separated, on the average, by the distances that are very large compared with their diameters

3 the molecules did not exert force on each other except when they collide 4 there is no preferred position for a molecule and no preferred direction for velocity,when there is no external force
3 the molecules did not exert force on each other except when they collide 4 there is no preferred position for a molecule and no preferred direction for velocity, when there is no external force
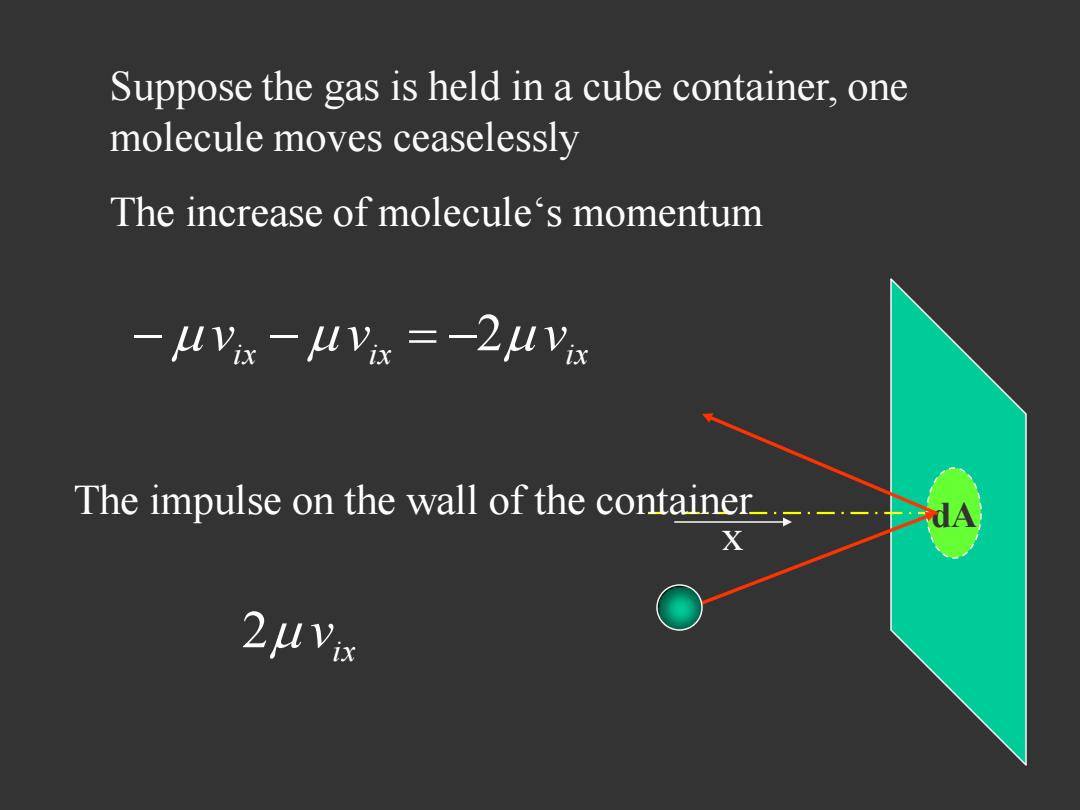
Suppose the gas is held in a cube container,one molecule moves ceaselessly The increase of molecule's momentum -MVis -MlVi =-2MVa The impulse on the wall of the container
x dA The increase of molecule‘s momentum i x i x i x v v 2 v The impulse on the wall of the container ix 2 v Suppose the gas is held in a cube container, one molecule moves ceaselessly
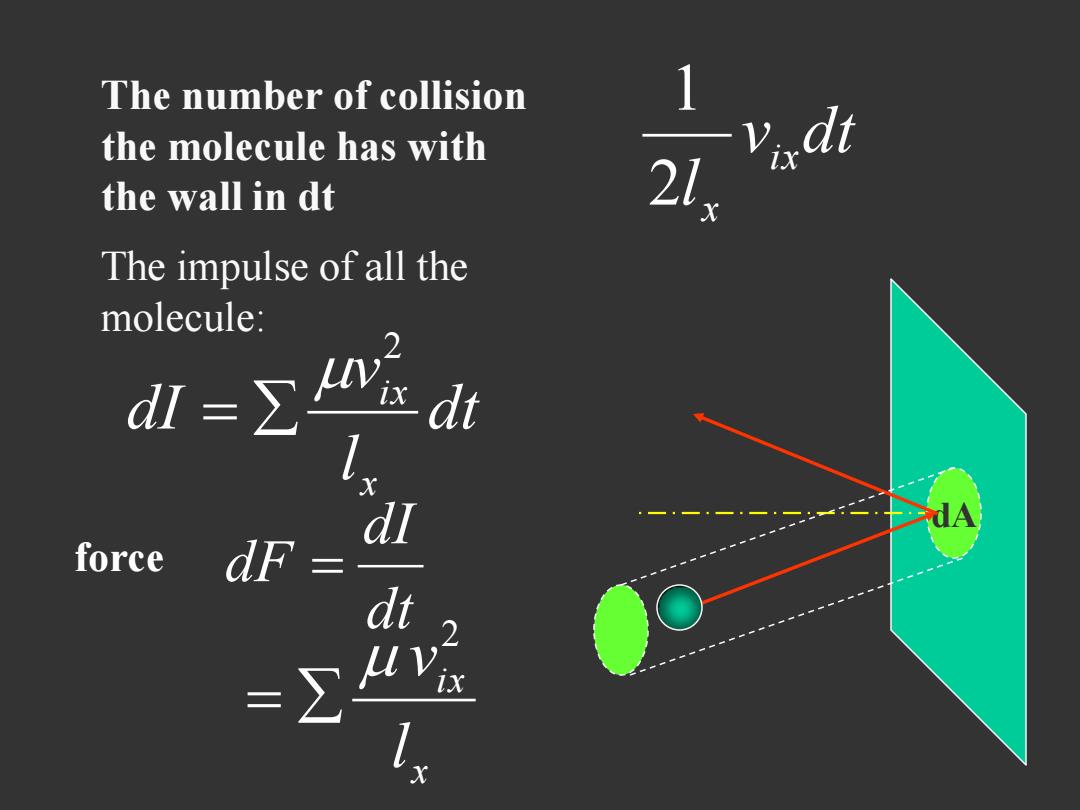
The number of collision the molecule has with the wall in dt The impulse of all the molecule: r dt d force dF dt
dA The number of collision the molecule has with the wall in dt v dt l ix x 2 1 dt l v dI x i x 2 force dt dI dF x ix l v 2 The impulse of all the molecule:
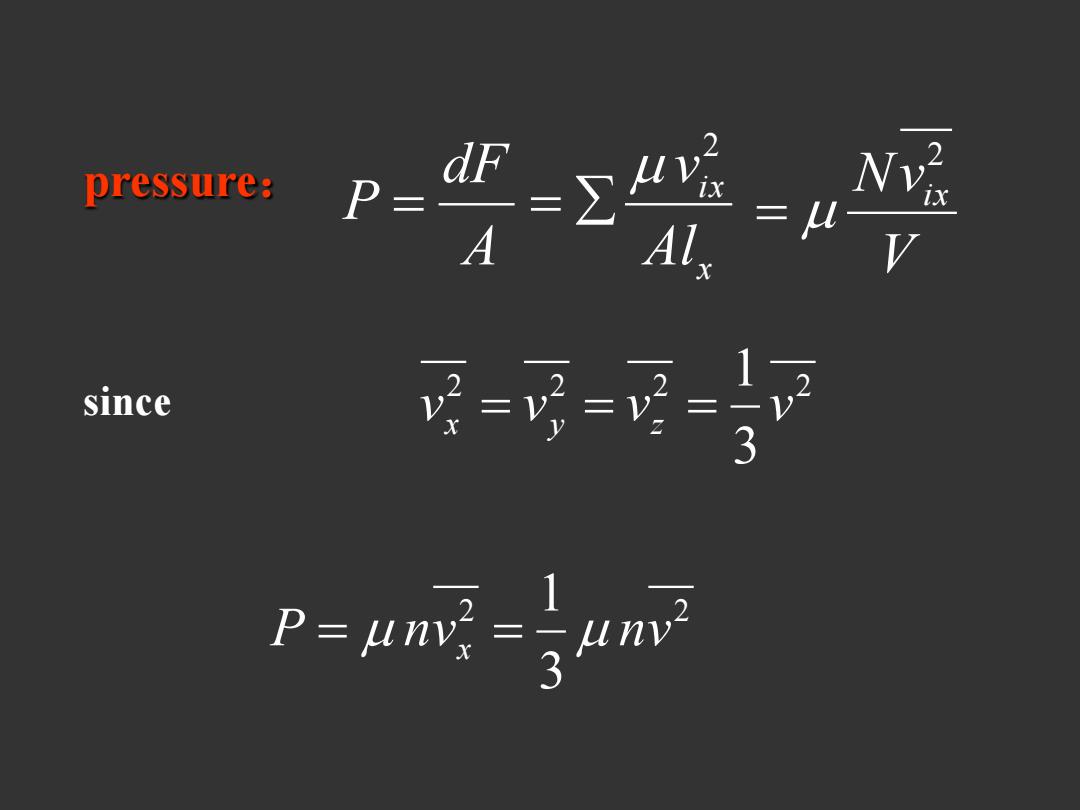
pressure: P=9 since ==- -nn
pressure: x i x Al v A dF P 2 V Nvix 2 since 2 2 2 2 3 1 v v v v x y z 2 2 3 1 P nv nv x