
Oscillations
Oscillations

Agenda Today 1 Simple harmonic motion 2 Pendulum 3 Damped harmonic motion
Agenda Today 1 Simple harmonic motion 2 Pendulum 3 Damped harmonic motion

Oscillation(振动): The movement that repeat itself Simple harmonic motion:(简谐振动) Any oscillation that could be expressed as a sinusoidal function
Oscillation(振动): The movement that repeat itself. Simple harmonic motion:(简谐振动) Any oscillation that could be expressed as a sinusoidal function

x=Acos(@t+p A:amplitude(振幅) p:phase constant(振动的“初位相”) (otp):phase(振动的“位相”) o:angular frequency(圆频率)
x Acos(t ) A :amplitude(振幅) :phase constant(振动的“初位相 ”) ( t+ ) :phase(振动的“位相 ”) :angular frequency(圆频率)

Frequency (频率)v:the number of oscillations that finished in one second. 2π Period(周期)T:the time needed to finish one oscillation 2π
Period (周期)T:the time needed to finish one oscillation 2 Frequency (频率):the number of oscillations that finished in one second. 1 2 T

Velocity and acceleration of SHM s+p)=eota+p+》 dx V= dt a 血=-02Acos(o1+p)=0.c0so1+9士π) 1、Vm=@4 velocity amplitude“速度幅”。 2、am=o2A acceleration amplitude m “加速度幅
) 2 sin( ) cos( A t v t dt dx v m cos( ) cos( ) 2 A t a t dt dv a m 1、 vm A velocity amplitude“速度幅 ”。 2、 acceleration amplitude “加速度幅 ”。 am A 2 Velocity and acceleration of SHM
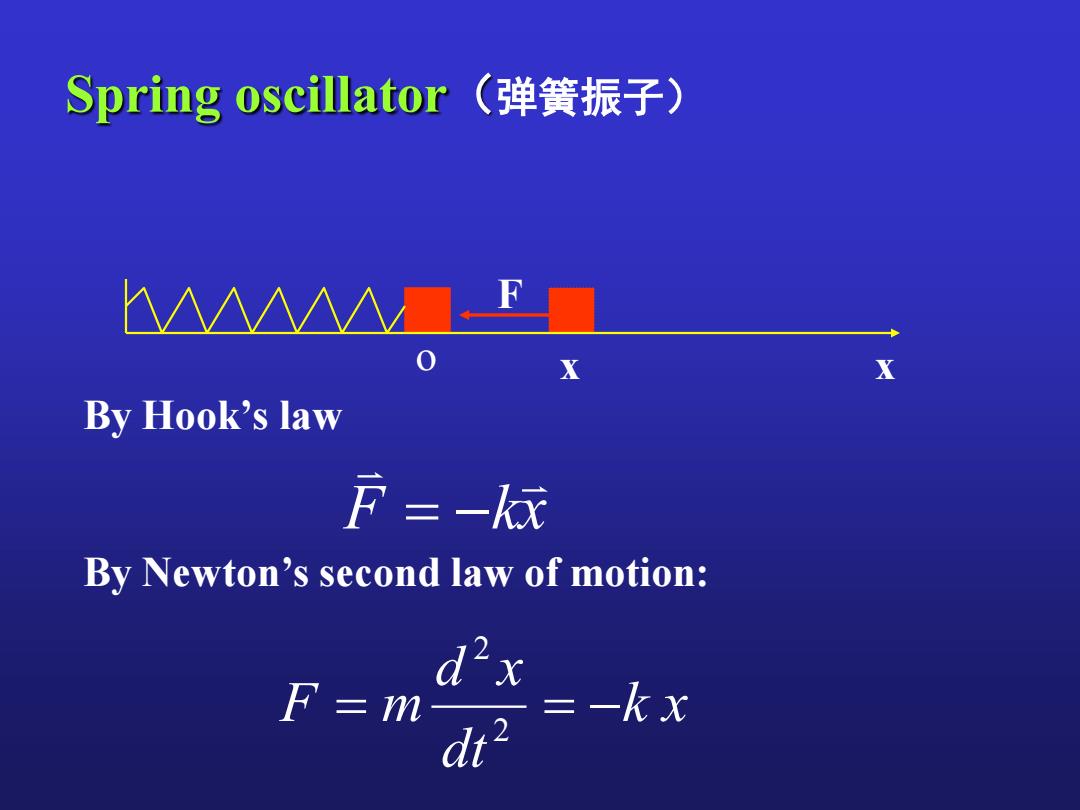
Spring oscillator(弹簧振子) △△△个个M X By Hook's law F=- By Newton's second law of motion: d'x F=m dt" =kx
Spring oscillator(弹簧振子) F By Hook’s law F kx o x x By Newton’s second law of motion: k x dt d x F m 2 2
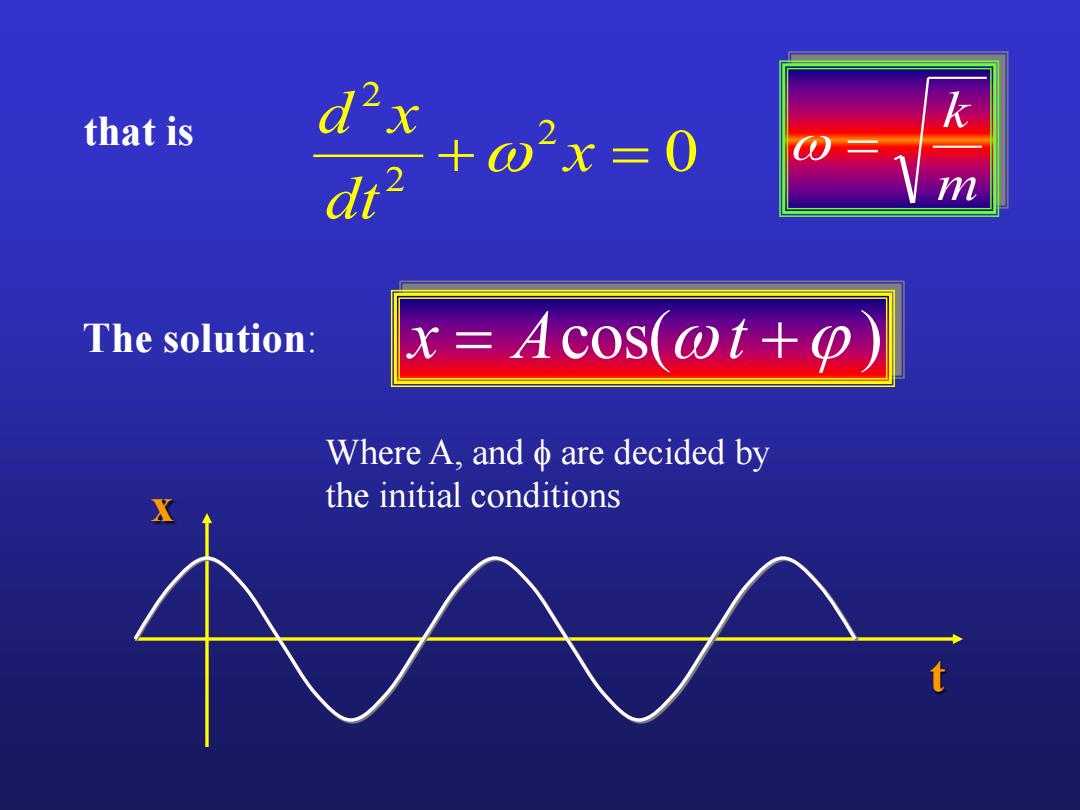
that is 0x=0 dt2 The solution: x=Acos(@t+o) Where A,and o are decided by the initial conditions
0 2 2 2 x dt d x that is x Acos(t ) x t m k Where A, and are decided by the initial conditions The solution:
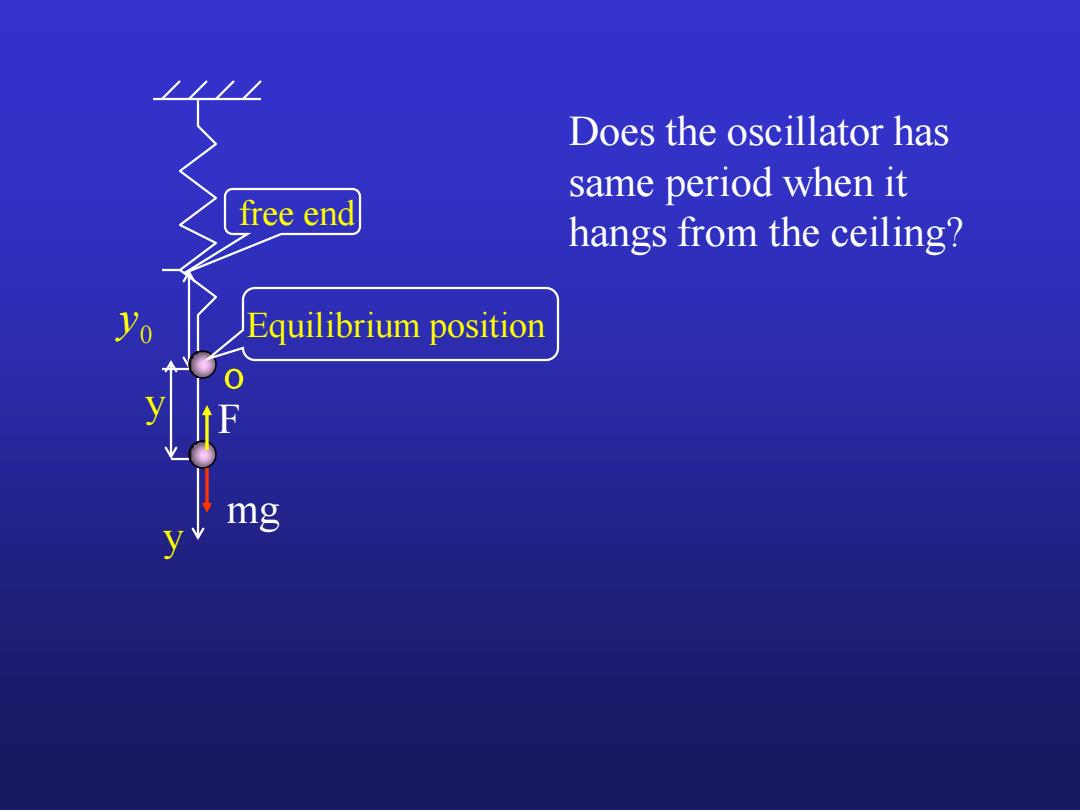
Does the oscillator has same period when it free end hangs from the ceiling? Yo Equilibrium position mg
0 y free end Equilibrium position y o y mg F Does the oscillator has same period when it hangs from the ceiling?
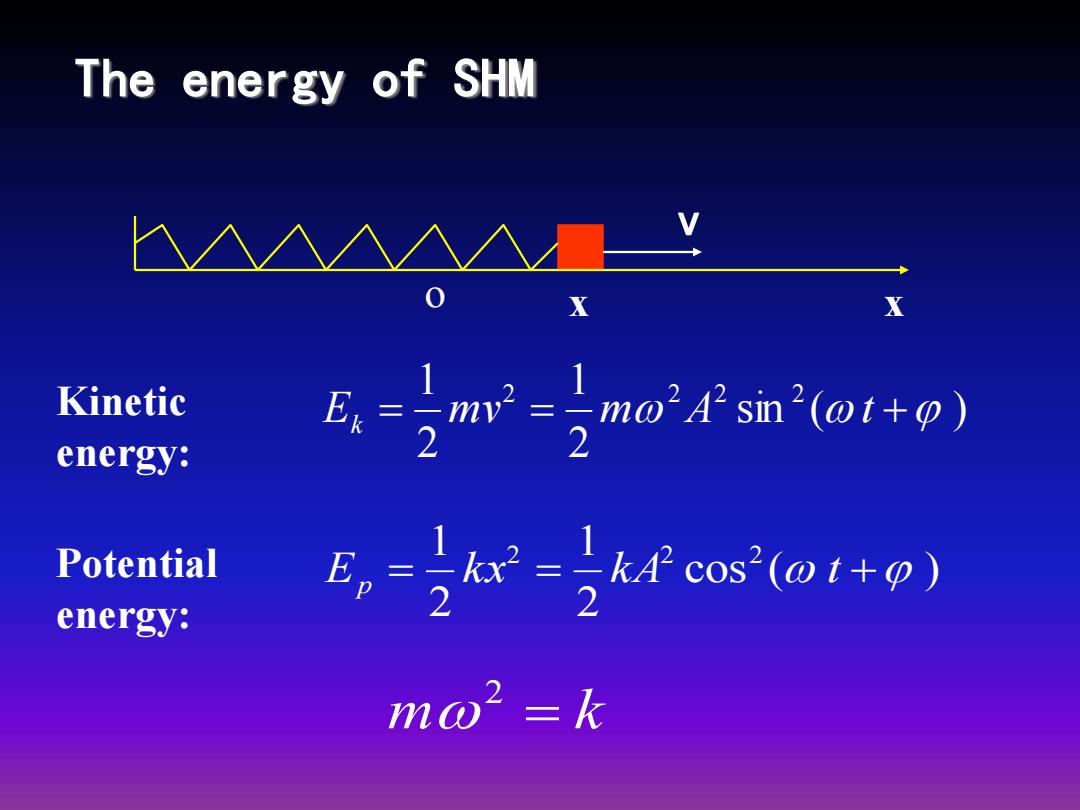
The energy of SHM X X Kinetic energy: 女-mmsi) Potential E-3k-3k cos() energy: mo2 k
The energy of SHM sin ( ) 2 1 2 1 2 2 2 2 Ek m v m A t cos ( ) 2 1 2 1 2 2 2 Ep k x k A t m k 2 Kinetic energy: Potential energy: o x x v