
motion of rigid body
motion of rigid body

Agenda today 1 rigid body,its kinetic energy 2 the moment of inertia 3 Newton's law of rotation
Agenda today 1 rigid body, its kinetic energy 2 the moment of inertia 3 Newton’s law of rotation

Rigid body(刚体): The object has a shape unchangeable A rigid body can be treated as a group of particles with their distance unchangeable
Rigid body(刚体): The object has a shape unchangeable A rigid body can be treated as a group of particles with their distance unchangeable
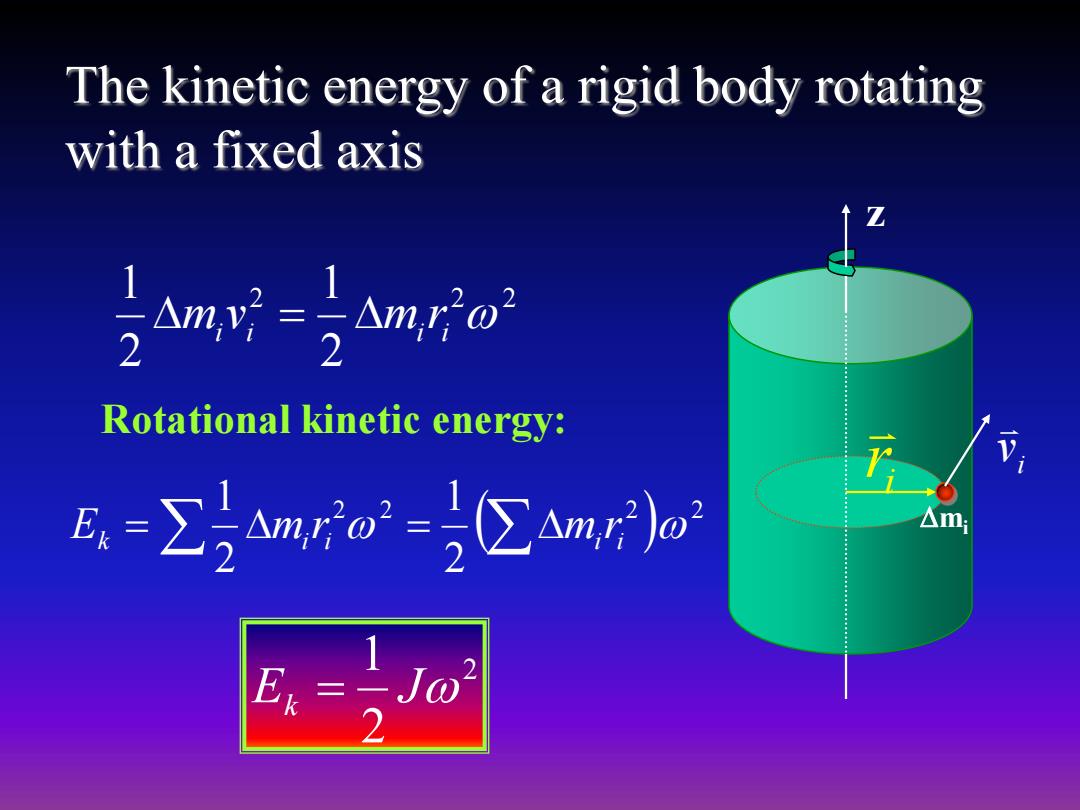
The kinetic energy of a rigid body rotating with a fixed axis 2n旷-nrio 2 Rotational kinetic energy: E-∑mo2=wy Ek
The kinetic energy of a rigid body rotating with a fixed axis 2 2 2 2 1 2 1 mi vi mi ri Rotational kinetic energy: 2 2 2 2 2 1 2 1 Ek mi ri mi ri 2 2 1 Ek J mi z i r i v

Moment of inertia(惯量) The inertia of the rigid body that is rotating definition J=∑△m,r2 A continuous body: J=Sr2dm the moment of inertia of one rigid body is determined by its shape the position of the axis and the density distribution
Moment of inertia(惯量) The inertia of the rigid body that is rotating definition 2 i i J m r A continuous body: J r dm2 the moment of inertia of one rigid body is determined by its shape , the position of the axis and the density distribution

Why did this ropewalker stretch his arms to keep balance?
Why did this ropewalker stretch his arms to keep balance?

The moment of inertia of rod with its mass distributed uniformly and a perpendicular axis through one of its ends (its length 1) Solution: J=x'dm dm=pds m dm 0 I m
The moment of inertia of rod with its mass distributed uniformly and a perpendicular axis through one of its ends (its length l) o x z dx dm x J x dm2 Solution: dx l m dm dx l l x l m dx l m J x 0 3 0 2 3 1 2 3 1 J ml

Find the moment of inertia of a uniform disk about axis through its center and perpendicular to the plane of the disk solution dm o 2n rdr J=∫rdm=2mo∫r J=2ra"rdr πoR41 2
Find the moment of inertia of a uniform disk about axis through its center and perpendicular to the plane of the disk solution: o r dr R dm 2 rdr J r dm2 r dr 3 2 R J r dr 0 3 2 2 4 2 1 2 mR R

(2)the paralle-axis theorem(平行轴原理) the moment of inertia when the axis is through the center of mass is J.,and the moment of inertia J,about a parallel axis a distance d away is: J.=J。+md For example: mR2 J=mR+mR爬mR2
m R Jz (2)the parallel-axis theorem(平行轴原理) the moment of inertia when the axis is through the center of mass is Jc,and the moment of inertia Jz about a parallel axis a distance d away is: 2 J J md z c Jc 2 2 1 Jc mR 2 2 2 1 Jz mR mR 2 2 3 mR For example:

In the game of judo,it is much easier to throw your opponent by rotating him around his hip,why?
In the game of judo, it is much easier to throw your opponent by rotating him around his hip, why?