19-1黑体辐射 普朗克能量子假设 第十九章量子物理 量子概念是1900年普朗克首先提出的,距今已 有一百多年的历史.其间,经过爱因斯坦、玻尔、德 布罗意、玻恩、海森伯、薛定谔、狄拉克等许多物理 大师的创新努力,到20世纪30年代,就建立了一 套完整的量子力学理论. 微观世界的理论 量子力学 起源于对波粒二相性的认识 宏观领域 量子力学 经典力学 量子力学 相对论 现代物理的理论基础
19 – 1 黑体辐射 普朗克能量子假设 第十九章 量子物理 量子概念是 1900 年普朗克首先提出的,距今已 有一百多年的历史.其间,经过爱因斯坦、玻尔、德 布罗意、玻恩、海森伯、薛定谔、狄拉克等许多物理 大师的创新努力,到 20 世纪 30 年代,就建立了一 套完整的量子力学理论. 量子力学 宏观领域 经典力学 现代物理的理论基础 量子力学 相 对 论 量子力学 微观世界的理论 起源于对波粒二相性的认识

19-1 黑体辐射 普朗克能量子假设 第十九章量子物理 黑体黑体辐射 (1)热辐射 实验证明不同温度下物体能发出 不同的电磁波,这种能量按频率的分布随温度而不同 的电磁辐射叫做热辐射. (2)单色辐射出射度 单位时间内从物体单位表 面积发出的频率在V附近单位频率区间(或波长在入 附近单位波长区间)的电磁波的能量· 单色辐射出射度M(T)单位:W/(m2.Hz) 单色辐射出射度Ma(T)单位:W/m3
19 – 1 黑体辐射 普朗克能量子假设 第十九章 量子物理 一 黑体 黑体辐射 (1)热辐射 实验证明不同温度下物体能发出 不同的电磁波,这种能量按频率的分布随温度而不同 的电磁辐射叫做热辐射. (2)单色辐射出射度 单位时间内从物体单位表 面积发出的频率在 附近单位频率区间(或波长在 附近单位波长区间)的电磁波的能量 . 单色辐射出射度 M (T) 单位:W/m3 单色辐射出射度 单位: W/(m Hz) 2 M (T)
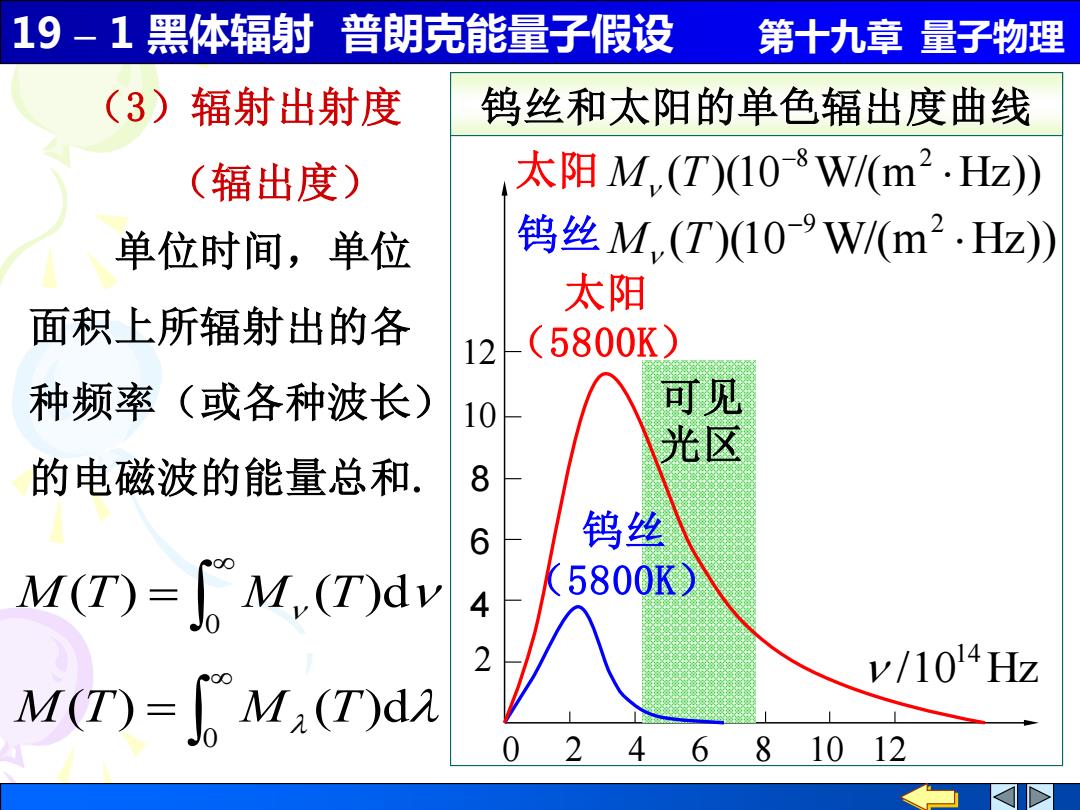
19-1 黑体辐射普朗克能量子假设 第十九章量子物理 (3)辐射出射度 钨丝和太阳的单色辐出度曲线 (辐出度) 太阳M.(T)108W/(m2.Hz) 单位时间,单位 钨丝M,(T)10-9W/(m2.Hz) 太阳 面积上所辐射出的各 12 (5800K) 种频率(或各种波长) 10 可见 光区 的电磁波的能量总和. 8 6 钨丝 M(T)=[M(T)dv (5800K) 4 2 v/1014Hz M(T)=M2(T)da 024 681012
19 – 1 黑体辐射 普朗克能量子假设 第十九章 量子物理 (3)辐射出射度 (辐出度) 单位时间,单位 面积上所辐射出的各 种频率(或各种波长) 的电磁波的能量总和. = 0 M(T) M (T)d 0 2 4 6 8 10 12/10 Hz 14 钨丝和太阳的单色辐出度曲线 2 12 10 4 6 8 ( )(10 W/(m Hz)) 8 2 − 太阳 M T 可见 光区 钨丝 (5800K) 太阳 (5800K) ( )(10 W/(m Hz)) 9 2 − 钨丝 M T = 0 M(T) M (T)d

19-1黑体辐射 普朗克能量子假设 第十九章量子物理 实验表明 辐射能力越强的物体,其吸收能力也越强。 (4)黑体 能完全吸收照射到它上面的各种频率 的电磁辐射的物体称为黑体,(黑体是理想模型) 黑体辐射与温度的关系→ K>
19 – 1 黑体辐射 普朗克能量子假设 第十九章 量子物理 实验表明 辐射能力越强的物体,其吸收能力也越强. (4)黑体 能完全吸收照射到它上面的各种频率 的电磁辐射的物体称为黑体 .(黑体是理想模型)
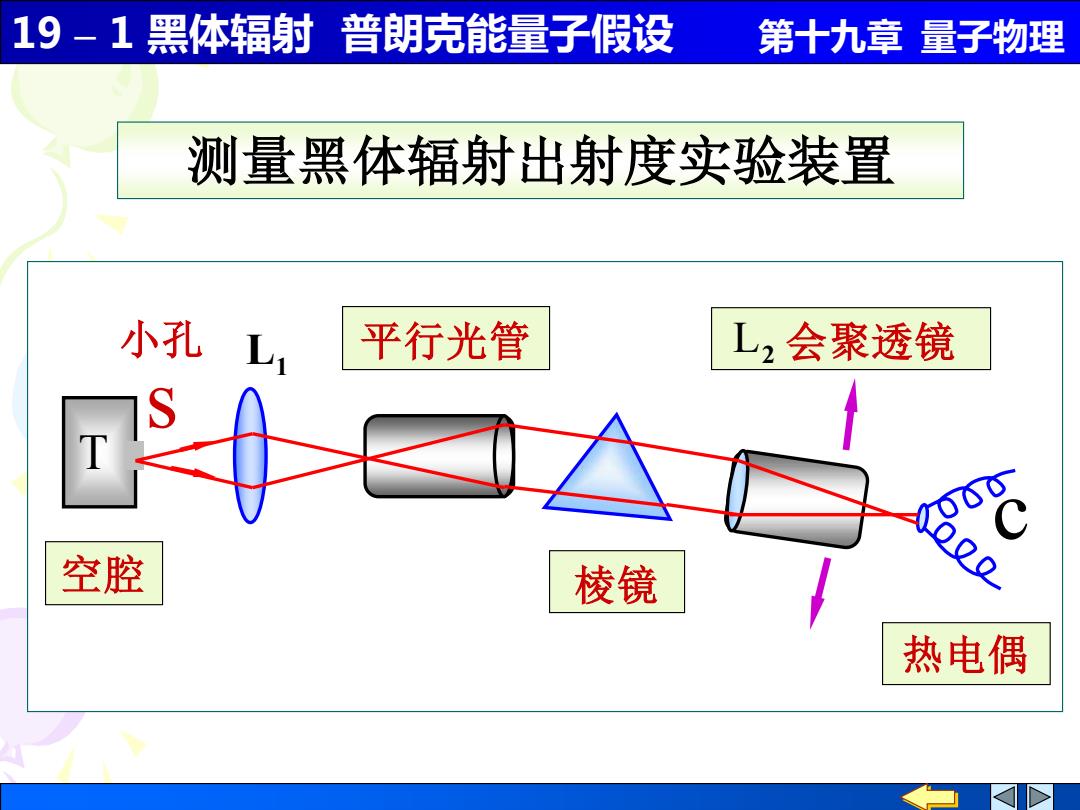
19-1黑体辐射普朗克能量子假设 第十九章量子物理 测量黑体辐射出射度实验装置 小孔 平行光管 L2会聚透镜 空腔 棱镜 热电偶
19 – 1 黑体辐射 普朗克能量子假设 第十九章 量子物理 T L1 s L2 会聚透镜 c 空腔 小孔 平行光管 棱镜 热电偶 测量黑体辐射出射度实验装置
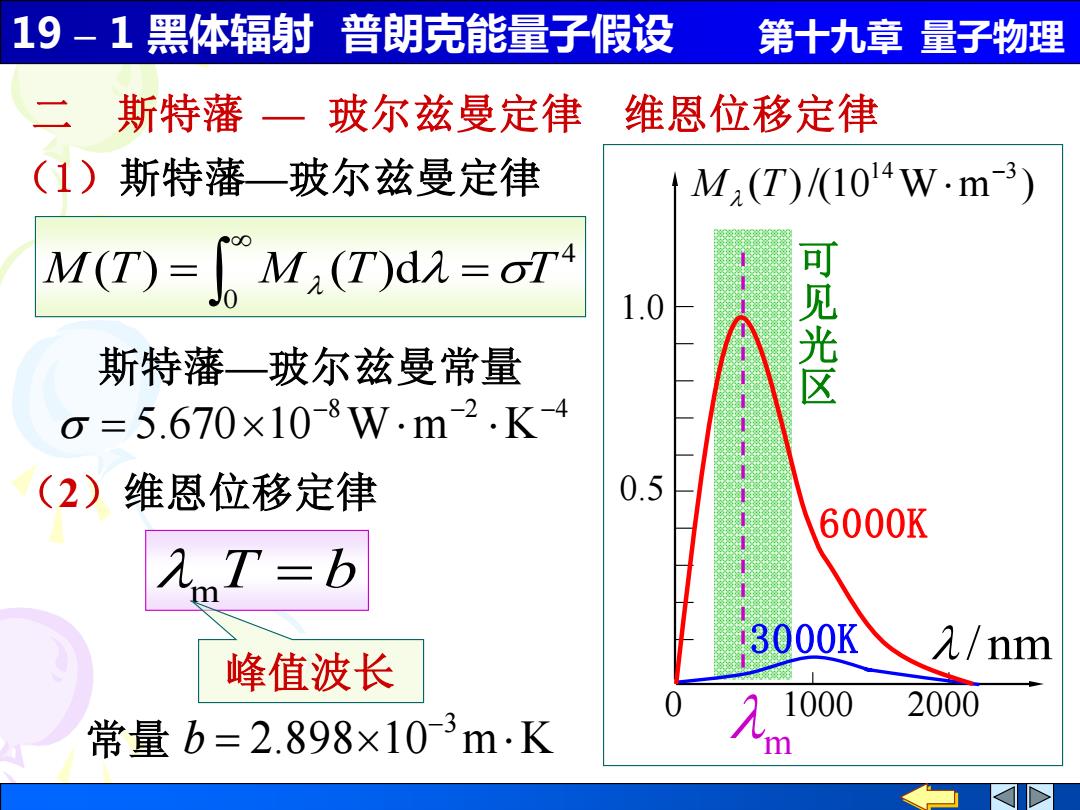
19-1 黑体辐射 普朗克能量子假设 第十九章量子物理 二斯特藩 一玻尔兹曼定律 维恩位移定律 (1)斯特藩一玻尔兹曼定律 M,(T)/1014W.m-3) M(T)=[M,(T)dA=oT4 1.0 可见 斯特藩—玻尔兹曼常量 0=5.670×10-8W.m2.K-4 (2)维恩位移定律 0.5 6000K T= b 3000K 元/nm 峰值波长 1000 2000 常量b=2.898×10-3m·K m
19 – 1 黑体辐射 普朗克能量子假设 第十九章 量子物理 0 1000 2000 1.0 0.5 ( )/(10 W m ) 14 −3 M T / nm 二 斯特藩 — 玻尔兹曼定律 维恩位移定律 可 见 光 区 3000K 6000K (1)斯特藩—玻尔兹曼定律 4 0 M(T) = M (T)d =T 8 2 4 5.670 10 W m K − − − = 斯特藩—玻尔兹曼常量 (2)维恩位移定律 m T = b 2.898 10 m K 3 = − 常量 b 峰值波长 m

19-1 黑体辐射普朗克能量子假设 第十九章量子物理 例1(1)温度为室温(20°C)的黑体,其单色辐 出度的峰值所对应的波长是多少?(2)若使一黑体 单色辐出度的峰值所对应的波长在红色谱线范围内, 其温度应为多少?(3)以上两辐出度之比为多少? 解(1)由维恩位移定律 b 2.898×10-3 m=9890nm 293 (2)取2m=650nm b T= 2.898×103 K=4.46×103K 九m 6.5×10-7 (3)由斯特藩一玻尔兹曼定律 M(T)/M(T)=(T/T)4=5.37×104
19 – 1 黑体辐射 普朗克能量子假设 第十九章 量子物理 nm 9890nm 293 2.898 10 3 m = = = − T b K 4.46 10 K 6.5 10 2.898 10 ' 3 7 3 m = = = − − b T 4 4 M(T') M(T) = (T' T) = 5.3710 例1 (1)温度为室温 的黑体,其单色辐 出度的峰值所对应的波长是多少?(2)若使一黑体 单色辐出度的峰值所对应的波长在红色谱线范围内, 其温度应为多少?(3)以上两辐出度之比为多少? (20 C) 解 (2)取 m = 650nm (1)由维恩位移定律 (3)由斯特藩—玻尔兹曼定律

19-1 黑体辐射 普朗克能量子假设 第十九章量子物理 例2太阳的单色辐出度的峰值波长2=483m, 试由此估算太阳表面的温度 解 由维恩位移定律 b 2.898×103 T= K≈6000K 483×109 对宇宙中其他发光星体的表面温度也可用 这种方法进行推测
19 – 1 黑体辐射 普朗克能量子假设 第十九章 量子物理 K 6000K 483 10 2.898 10 9 3 m = = − − b T 例2 太阳的单色辐出度的峰值波长 , 试由此估算太阳表面的温度. m = 483nm 解 由维恩位移定律 对宇宙中其他发光星体的表面温度也可用 这种方法进行推测
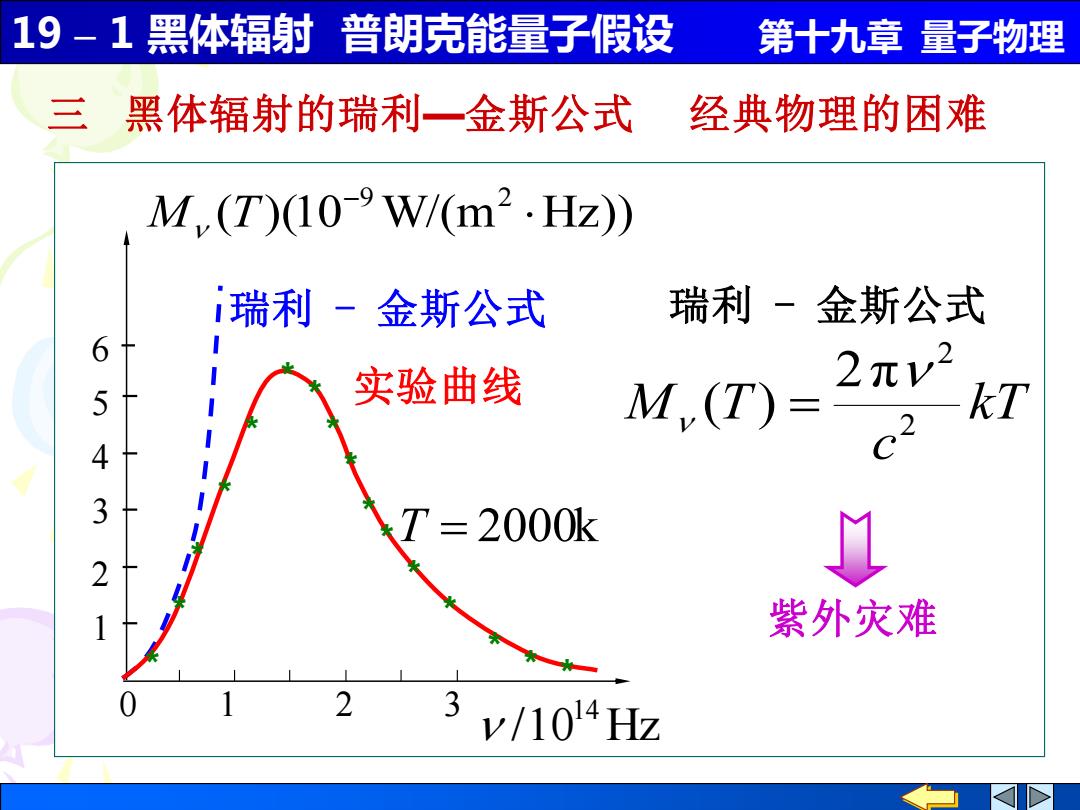
19-1 黑体辐射普朗克能量子假设 第十九章量子物理 三 黑体辐射的瑞利一金斯公式 经典物理的困难 M,(T)10-9W/(m2.Hz) 瑞利-金斯公式 瑞利-金斯公式 6 实验曲线 M.(7)= 2元y2 kT c2 T=2000k 紫外灾难 y/104Hz 3
19 – 1 黑体辐射 普朗克能量子假设 第十九章 量子物理 ( )(10 W/(m Hz)) 9 2 − M T 0 1 2 3 6 /10 Hz 14 1 2 3 4 5 瑞利 - 金斯公式 实验曲线 T = 2000k * * * * * * * * * * * * * * * * 三 黑体辐射的瑞利—金斯公式 经典物理的困难 kT c M T 2 2 2π ( ) = 瑞利 - 金斯公式 紫外灾难

19-1黑体辐射普朗克能量子假设 第十九章量子物理 四 普朗克假设普朗克黑体辐射公式(1900年) 普朗克认为:金属空腔壁中电子的振动可视为一 维谐振子,它吸收或者发射电磁辐射能量时,不是过 去经典物理认为的那样可以连续的吸收或发射能量, 而是以与振子的频率成正比的 能量子£=hv为单元来吸 6hv 收或发射能量.空腔壁上的带 5hv 电谐振子吸收或发射能量应为 4hv E=nhv(n=1,2,3,) 3hv 2hv 普朗克常量 1hv h=6.6260755×10-34J.s 2元h 普朗克黑体辐射公式M,(T)dv= -1
19 – 1 黑体辐射 普朗克能量子假设 第十九章 量子物理 四 普朗克假设 普朗克黑体辐射公式(1900 年) 6.6260755 10 J s 34 = − h 普朗克常量 能量子 = h 为单元来吸 收或发射能量. 普朗克认为:金属空腔壁中电子的振动可视为一 维谐振子,它吸收或者发射电磁辐射能量时,不是过 去经典物理认为的那样可以连续的吸收或发射能量, 而是以与振子的频率成正比的 1h 2h 3h 4h 5h 6h e 1 2π d ( )d / 3 2 − = h kT c h M T 普朗克黑体辐射公式 = nh (n =1,2,3, ) 空腔壁上的带 电谐振子吸收或发射能量应为