高等教育出版社：《物理学教程》教材电子教案（PPT课件，马文蔚第四版）第十七章 波动光学 17-07 单缝衍射

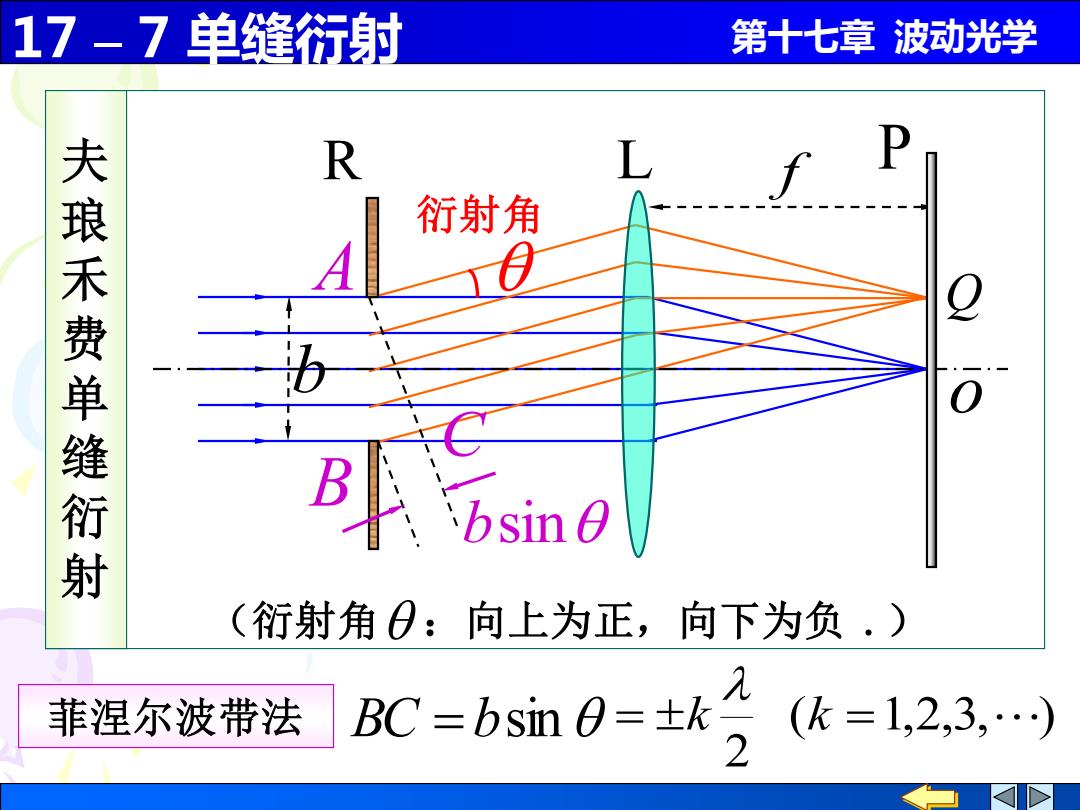
17-7单缝衍射 第十七章波动光学 R 衍射角 琅不费单缝衍射 B 'bsin O (衍射角0：向上为正，向下为负.) 菲涅尔波带法BC=bsin 0=±k (k=1,2,3,…)

17 – 7 单缝衍射 第十七章 波动光学 夫 琅 禾 费 单 缝 衍 射  衍射角 （衍射角  ：向上为正，向下为负 .） b BC = bsin ( 1,2,3, ) 2 = k k =   o L f R P A B bsin Q C 菲涅尔波带法

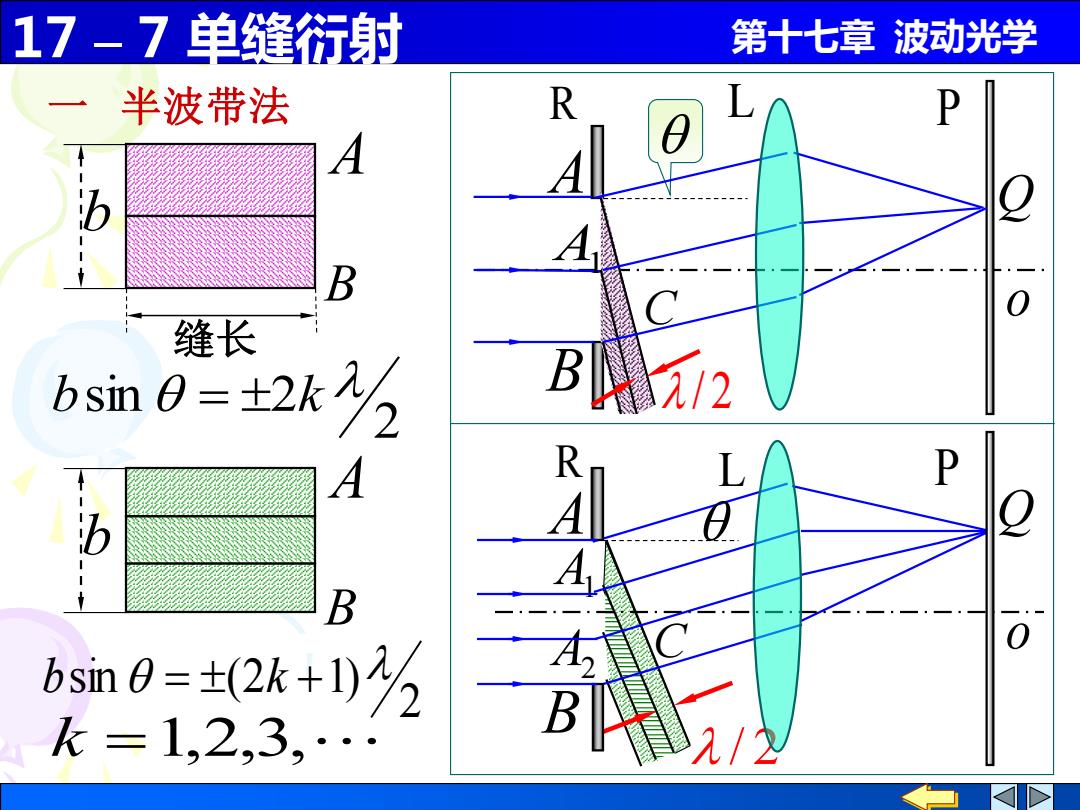
17-7单缝衍射 第十七章波动光学 半波带法 R b 缝长 bsim0=±2k 2/2 A b bsm0=±2k+03 k=1,2,3

17 – 7 单缝衍射 第十七章 波动光学 o R P A B Q  2 bsin  = 2k  2 bsin  = (2k +1)  一 半波带法 k =1,2,3,  A1 A2 C  / 2 b A B b 缝长 A B o A Q B  R L P C A1  / 2 L

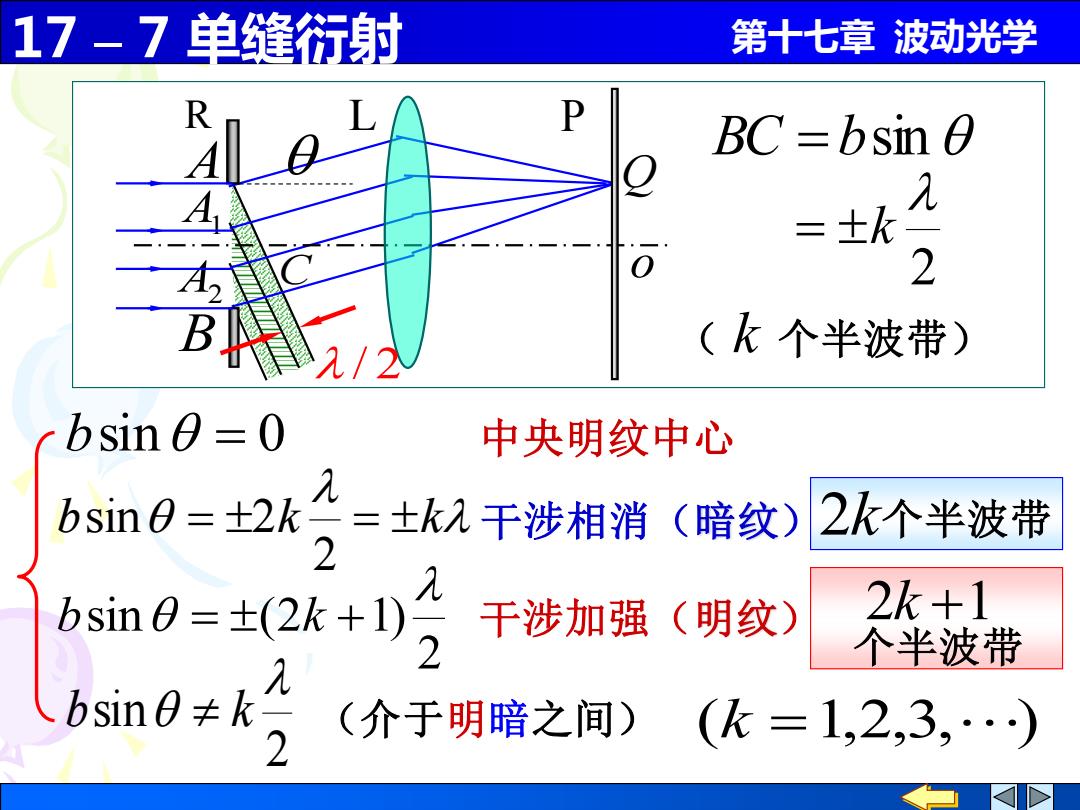
17-7单缝衍射 第十七章波动光学 BC=bsin 0 几 2 (k个半波带) bsin0=0 中央明纹中心 bsin0=+2k =±k入干涉相消（暗纹） 2k个半波带 2 bsim0=±(2k+1)2 干涉加强（明纹） 2k+1 个半波带 bsin0≠k 2 (介于明暗之间) (k=1,2,3,)

17 – 7 单缝衍射 第十七章 波动光学 (k =1,2,3, )   b  =  k = k 2 sin 2 干涉相消（暗纹） 2 sin (2 1)  b  =  k + 干涉加强（明纹） 2 sin  b   k （介于明暗之间） L o R P A Q B A1 A2  C  / 2 BC = bsin 2  = k （ k 个半波带） 2k 个半波带 个半波带 2k +1 bsin = 0 中央明纹中心

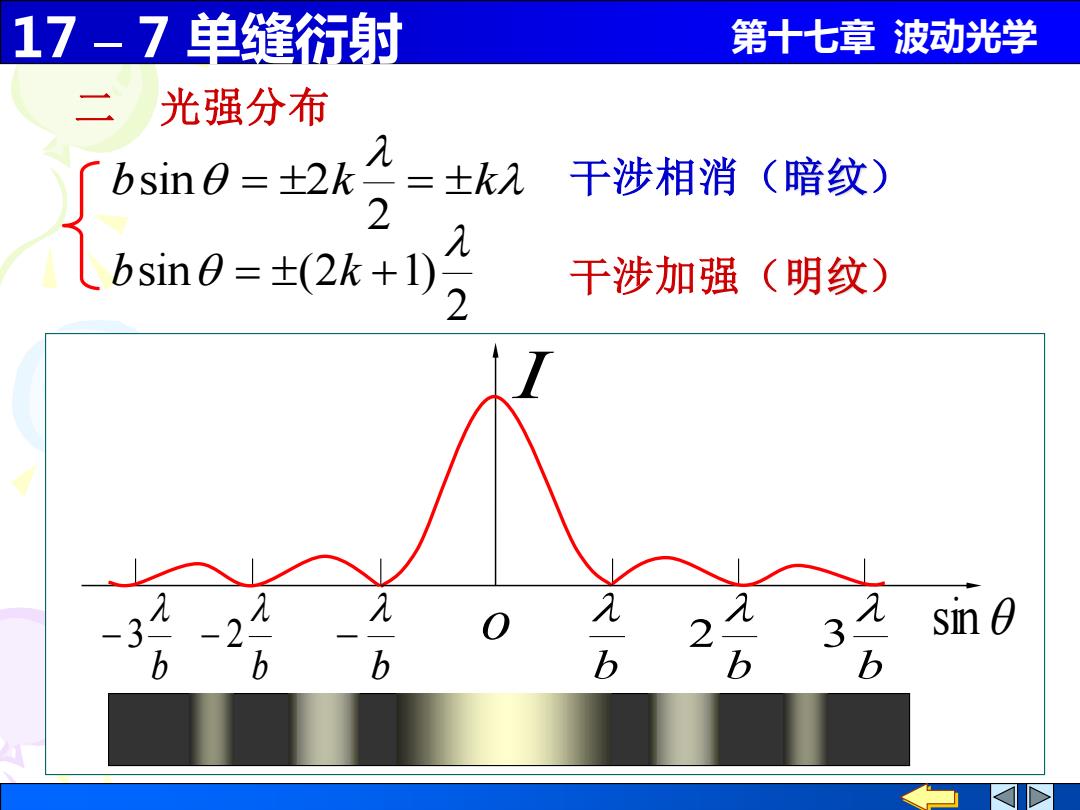
17-7单缝衍射 第十七章波动光学 二光强分布 Cbsine=+2k =±k入 干涉相消（暗纹） 2 Lbsin=(2k+1) 干涉加强（明纹） si 0

17 – 7 单缝衍射 第十七章 波动光学 sin  I o b  b  2 b  3 b  − b  − 2 b  − 3 二 光强分布   b  =  k = k 2 sin 2 干涉相消（暗纹） 2 sin (2 1)  b  =  k + 干涉加强（明纹）

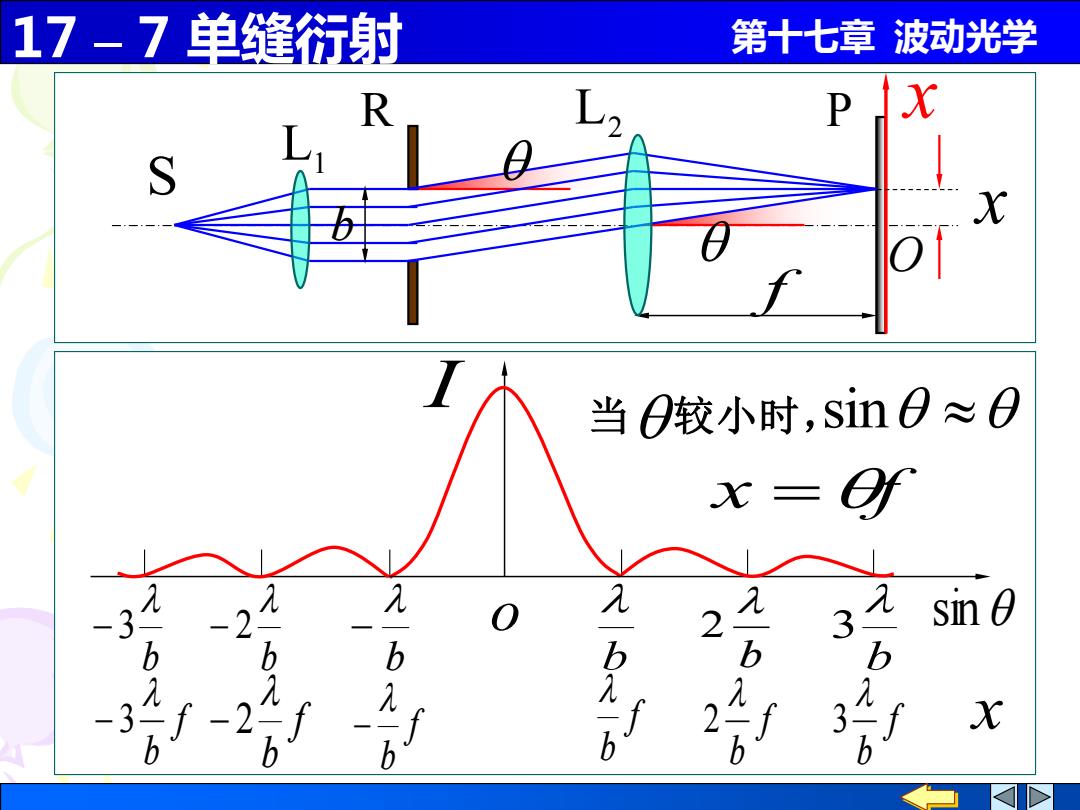
17-7单缝衍射 第十七章波动光学 R D X X 当0较小时，sin0≈0 2 3 sin 0 b b b 2 3 X b

17 – 7 单缝衍射 第十七章 波动光学 sin  I o b  b  2 b  3 b  − b  − 2 b  − 3 L1 L2 f  b S R P  O x x sin  x =f 当  较小时， f x b  f b  − f b  f 2 b  f − 2 b  − 3 f b  3

17-7单缝衍射 第十七章波动光学 bsin0=±2k。=±k2干涉相消（暗纹） 讨论 bim0=±(2k+D是7 2 干涉加强（明纹） sin0≈0，x= /,bsin0≈bx (1)第一暗纹距中心的距离 x,= 第一暗纹的衍射角 arcsin b

17 – 7 单缝衍射 第十七章 波动光学 R L P b o  f sin   , x =f , f x bsin  b   b  =  k = k 2 sin 2 干涉相消（暗纹） 2 sin (2 1)  b  =  k + 干涉加强（明纹） 讨 论 （1）第一暗纹距中心的距离 f b x f  1 = = 第一暗纹的衍射角 b  1 = arcsin x

17-7单缝衍射 第十七章波动光学 几 第一暗纹的衍射角 0,arcsin b →0 ◆九一定 了b增大，0减小60,8 光直线传播 b减小，0增大b→元，8， 2 衍射最大 ◆b一定，几越大，日越大，衍射效应越明显. (2)中央明纹 (k=1的两暗纹间) 角范围- sin< 线范围 b 中央明纹的宽度1，=2x,≈2

17 – 7 单缝衍射 第十七章 波动光学 b 一定，  越大， 越大，衍射效应越明显.  1  0,1  0 光直线传播  b b 增大，  1 减小  一定 b 减小，  1 增大 2 π , b   1  衍射最大 b  第一暗纹的衍射角 1 = arcsin 角范围 b b    −  sin  线范围 f b f x b   −   中央明纹的宽度 f b l x  0 = 2 1  2 （2）中央明纹 （ k =1 的两暗纹间）

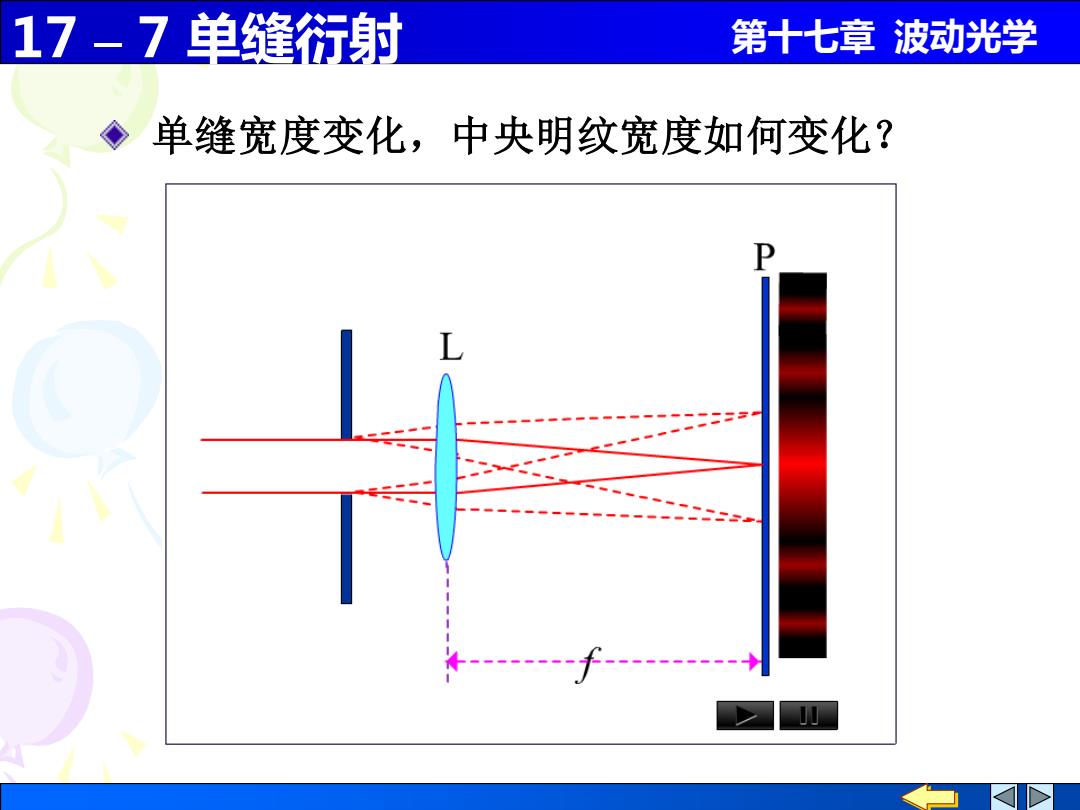
17-7单缝衍射 第十七章波动光学 ◆单缝宽度变化，中央明纹宽度如何变化？

17 – 7 单缝衍射 第十七章 波动光学 单缝宽度变化，中央明纹宽度如何变化？

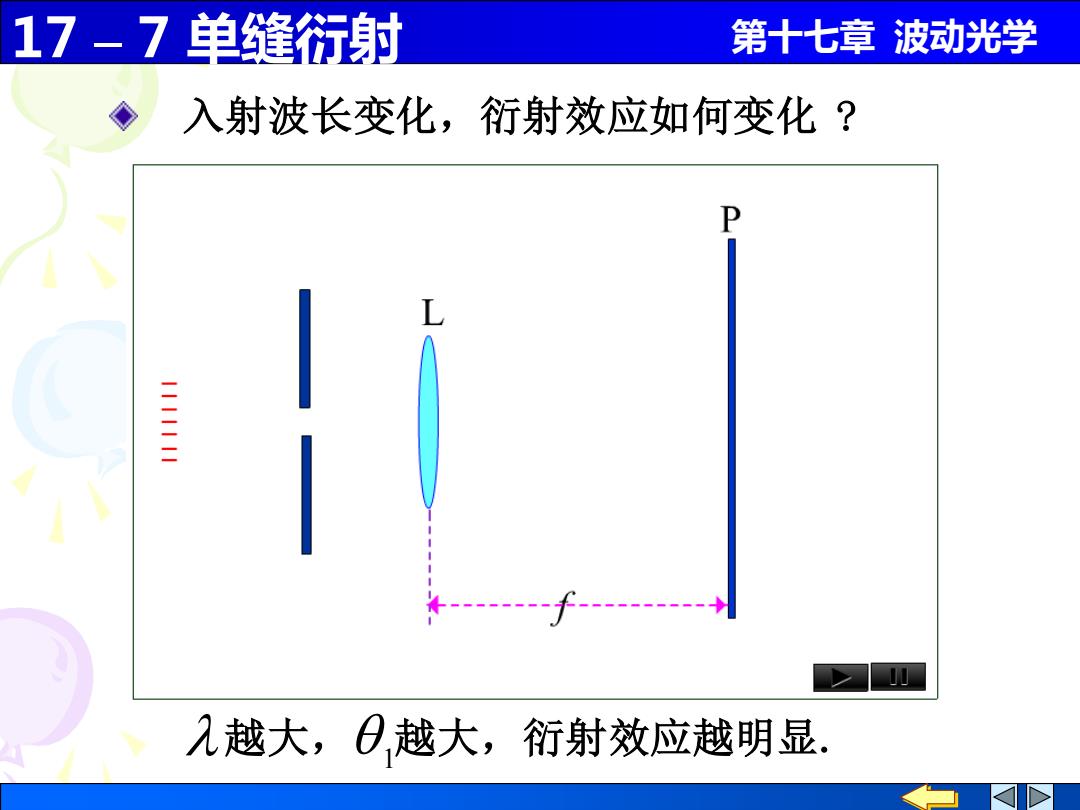
17-7单缝衍射 第十七章波动光学 入射波长变化，衍射效应如何变化？ 入越大，，越大，衍射效应越明显

17 – 7 单缝衍射 第十七章 波动光学 越大， 越大，衍射效应越明显.  1 入射波长变化，衍射效应如何变化 ?

17-7单缝衍射 第十七章波动光学 (3) 条纹宽度（相邻条纹间距） ±k入干涉相消（暗纹） 2 bsin0=±(2k+1) 干涉加强（明纹） 2 1=0%+f-0f= 九f 除了中央明纹外的其 b 它明纹、暗纹的宽度 (4)单缝衍射的动态变化 ◆ 单缝上下移动，根据透镜成像原理衍射图不变 单缝上移，零级明 纹仍在透镜光轴上

17 – 7 单缝衍射 第十七章 波动光学 o R f （4）单缝衍射的动态变化 单缝上移，零级明 纹仍在透镜光轴上. 单缝上下移动，根据透镜成像原理衍射图不变 . （3）条纹宽度（相邻条纹间距）   b  =  k = k 2 sin 2 干涉相消（暗纹） 2 sin (2 1)  b  =  k + 干涉加强（明纹） b f l f f k 1 k  = + − = 除了中央明纹外的其 它明纹、暗纹的宽度