15-6驻波 第十五章机械波 驻波的产生 振幅、频率、传播速度都相同的两列相干波,在 同一直线上沿相反方向传播时叠加而形成的一种特殊 的干涉现象
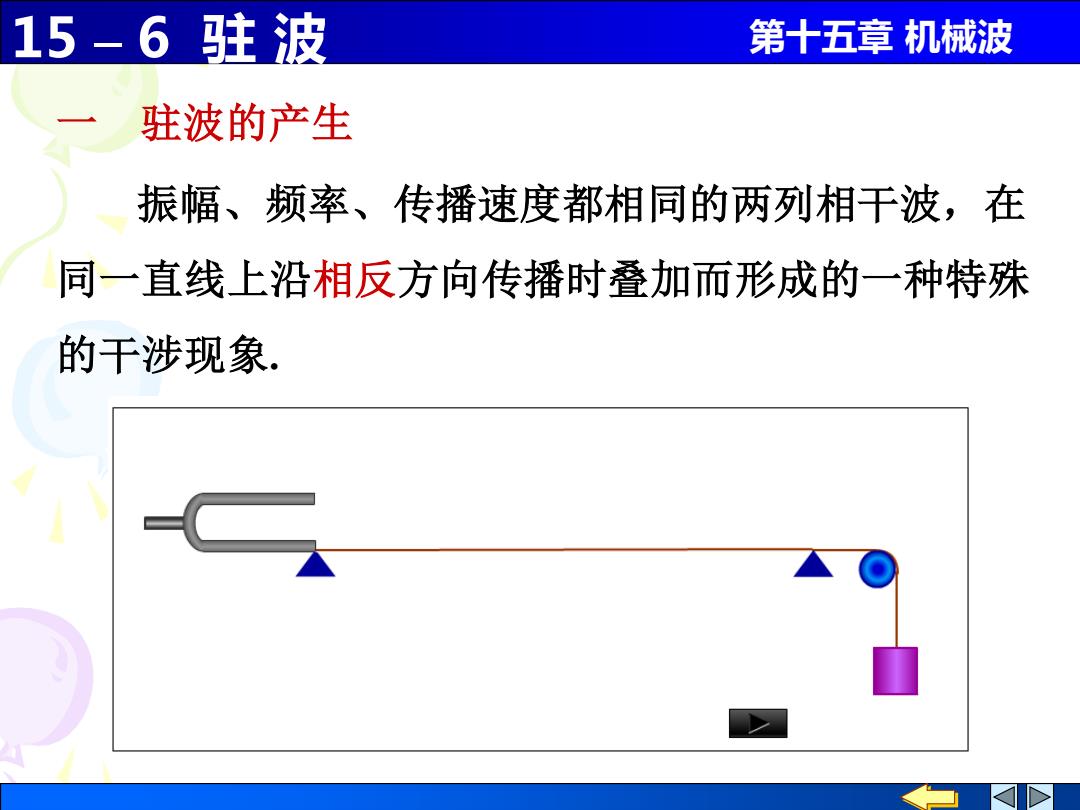
15 – 6 驻 波 第十五章 机械波 一 驻波的产生 振幅、频率、传播速度都相同的两列相干波,在 同一直线上沿相反方向传播时叠加而形成的一种特殊 的干涉现象
15-6驻波 第十五章机械波 驻波的形成 t=0 t=1/8T t=1/4T t=3/8T t=1/2T
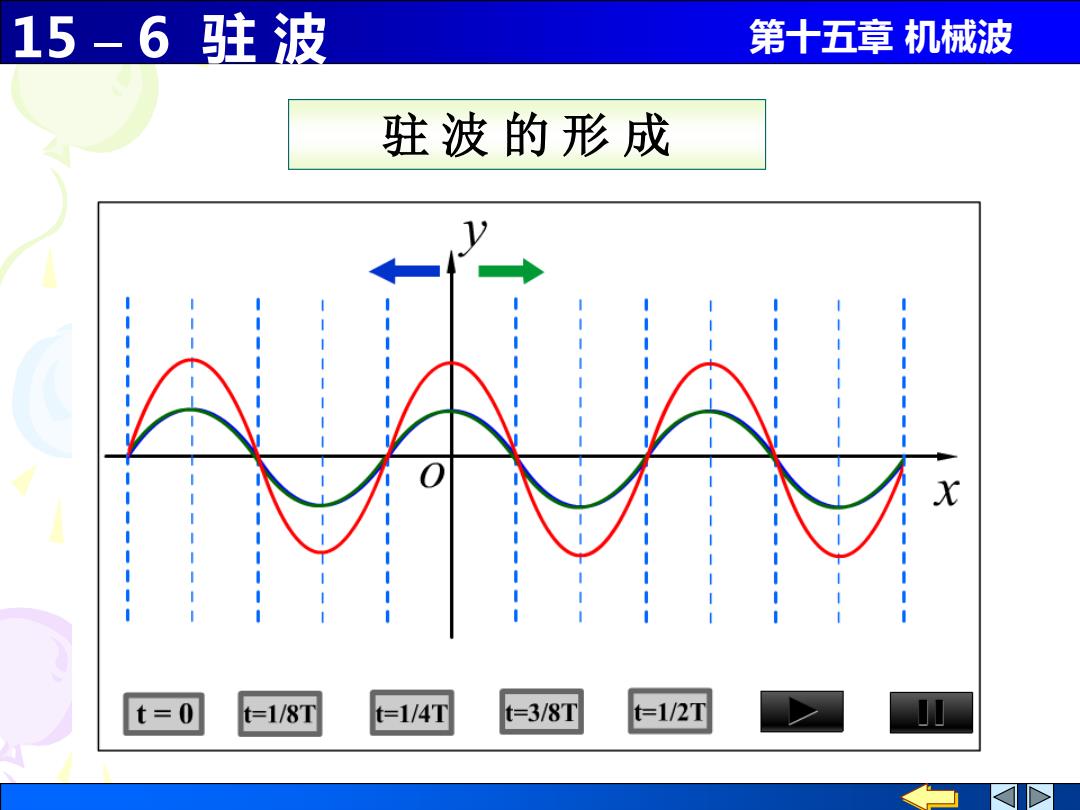
15 – 6 驻 波 第十五章 机械波 驻 波 的 形 成

15-6驻波 第十五章机械波 二 驻波方程 正向 4=1cos2x0-之 负向y2=Acos2玩(t+ y=y+y2 =Acos2r(t-克)+Acos2r(f+) =2Ac0s2元 coS2元vt 驻波的振幅 各质点都在作同 与位置有关 频率的简谐运动
15 – 6 驻 波 第十五章 机械波 驻波的振幅 与位置有关 t x A = 2 cos 2π cos 2π 二 驻波方程 cos 2π ( ) 1 x 正向 y = A t − cos 2π ( ) 2 x 负向 y = A t + 1 2 y = y + y 各质点都在作同 频率的简谐运动 cos 2π ( ) cos 2π ( ) x A t x = A t − + +

15-6驻波 第十五章机械波 X 讨论 > 驻波方程y=2Ac0S2π。c0S2元t 1)振幅 2Ac0s2π 随x而异,与时间无关 X 2元1 =±k元k=0,1,2,. cos2π 2π =k+2) k=0,1,2,… k=0,1, Amx =2A 波腹 (K+ K=0汀…=0 波节 相邻波腹(节)间距=几/2 相邻波腹和波节间距=2/4
15 – 6 驻 波 第十五章 机械波 t x y A 讨论 ➢ 驻波方程 = 2 cos 2π cos 2π = x cos 2π 2π = k π k = 0,1,2, x )π 0,1,2, 2 1 2π = (k + k = x 1 0 x = 波腹 0,1, 0 2 ) 2 1 ( k + k = Amin = 波节 k k 0,1, A 2A 2 = max = 相邻波腹(节)间距 = 2 相邻波腹和波节间距 = 4 1)振幅 随 x 而异, 与时间无关. x 2Acos 2π
15-6驻波 第十五章机械波 2)相邻两波节之间质点振动同相位,任一波节 两侧振动相位相反,在波节处产生兀的相位跃变. (与行波不同,无相位的传播) X y=2Acos2m,cos2元Vt 例x=士 为波节 4 X C0s2元 >0 Kx<y=2Ac0s2元c0s2元k X 4 X C0s2π <X< 2Acos2元c0s(2元V1+π) 4
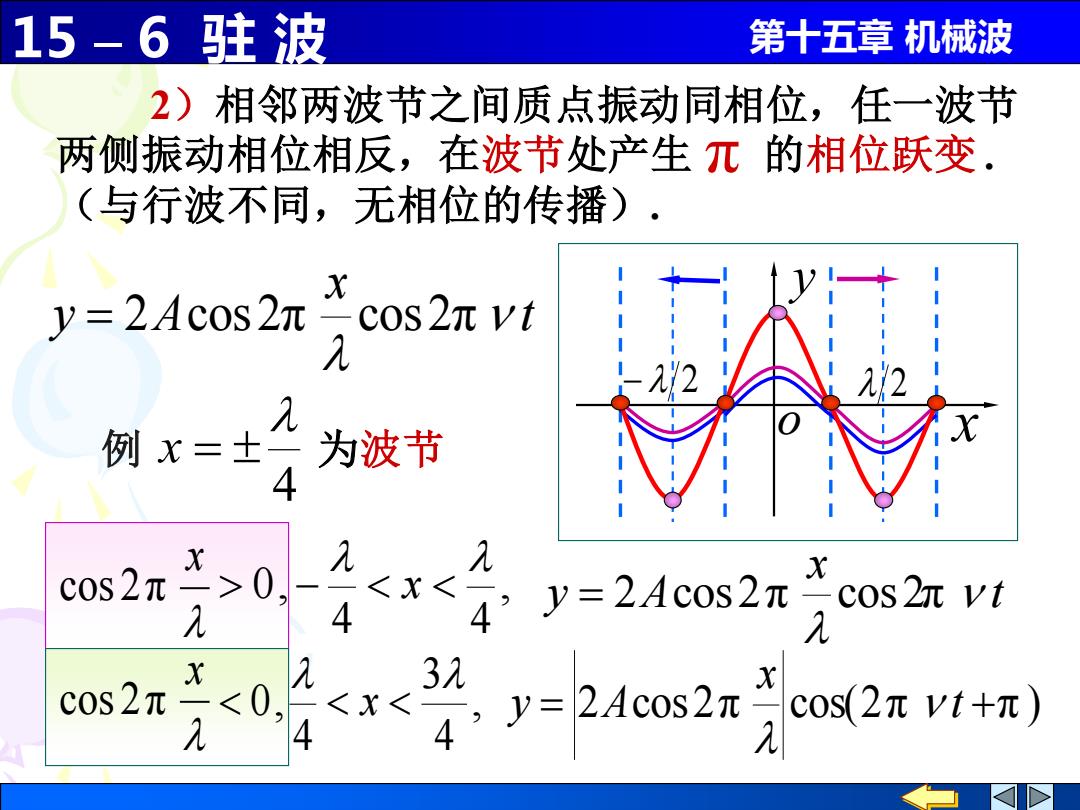
15 – 6 驻 波 第十五章 机械波 2)相邻两波节之间质点振动同相位,任一波节 两侧振动相位相反,在波节处产生 的相位跃变 . (与行波不同,无相位的传播). π t x y A = 2 cos2π cos2π x cos 2π , 4 4 0, − x t x y A = 2 cos2π cos2π = 2 cos2π cos(2π t +π ) x y A , 4 3 4 0, x x cos 2π x y o − 2 2 4 例 x = 为波节
15-6驻波 第十五章机械波 三 相位跃变(半波损失) 波疏介质 波密介质 波密介质较大 较小 当波从波疏介质垂直入射到波密介质,被反射 到波疏介质时形成波节.入射波与反射波在此处的相 位时时相反,即反射波在分界处产生兀的相位跃变, 相当于出现了半个波长的波程差,称半波损失
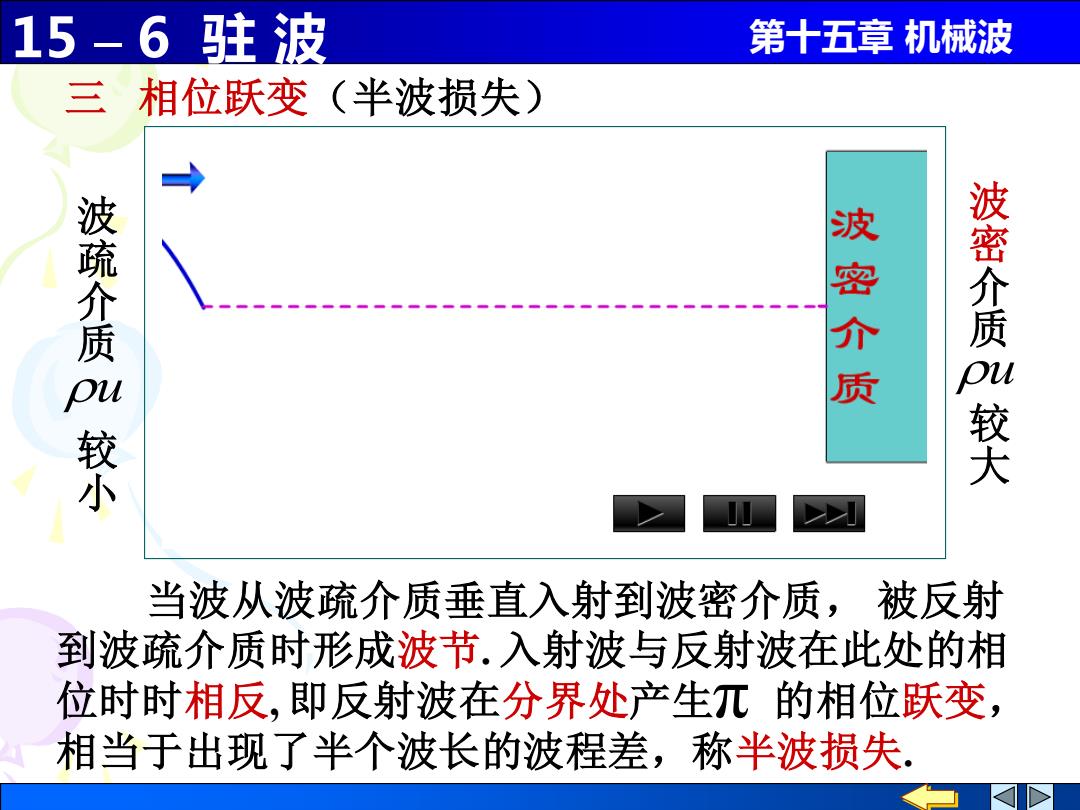
15 – 6 驻 波 第十五章 机械波 三 相位跃变(半波损失) 当波从波疏介质垂直入射到波密介质, 被反射 到波疏介质时形成波节. 入射波与反射波在此处的相 位时时相反, 即反射波在分界处产生 的相位跃变, 相当于出现了半个波长的波程差,称半波损失. π 波 密 介 质 u 较 大 波 疏 介 质 较 小 u
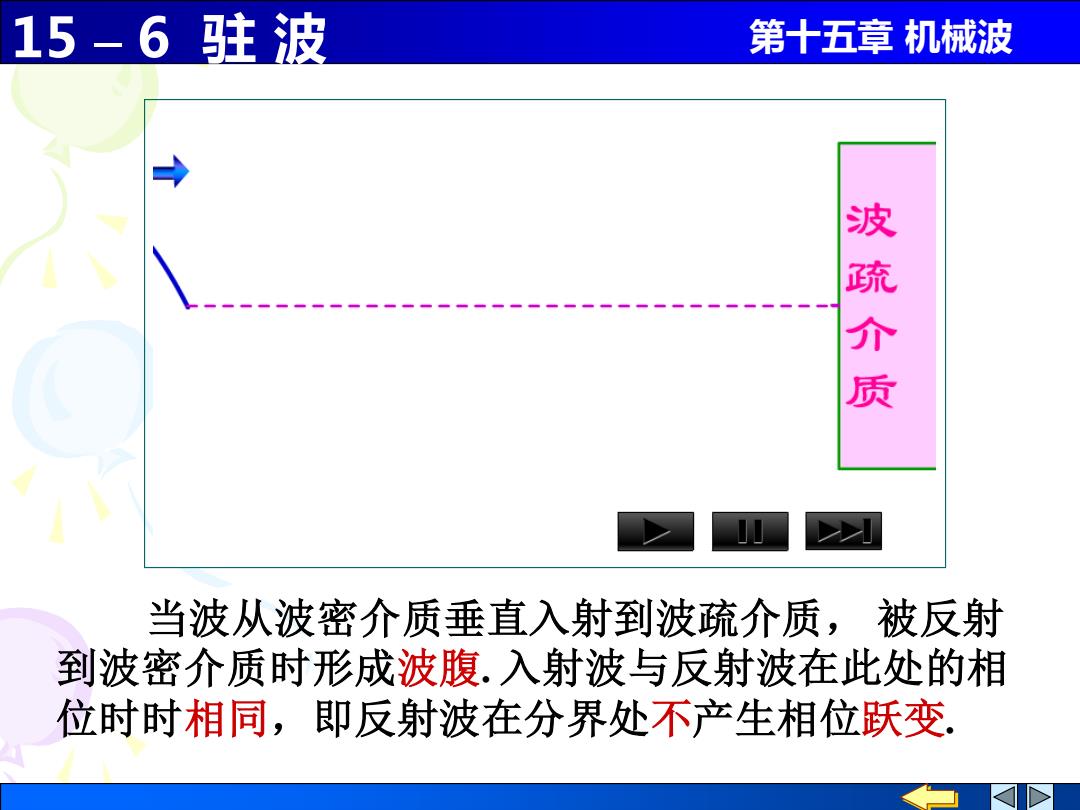
15-6驻波 第十五章机械波 介质 当波从波密介质垂直入射到波疏介质,被反射 到波密介质时形成波腹.入射波与反射波在此处的相 位时时相同,即反射波在分界处不产生相位跃变
15 – 6 驻 波 第十五章 机械波 当波从波密介质垂直入射到波疏介质, 被反射 到波密介质时形成波腹. 入射波与反射波在此处的相 位时时相同,即反射波在分界处不产生相位跃变

15-6驻波 第十五章机械波 四 驻波的能量 位移最大时 波 dW。oc 谈 X dx( A B C 平衡位置时 驻波的能量在相邻的波腹和波节间往复变化, 在相邻的波节间发生动能和势能间的转换,动能 主要集中在波腹,势能主要集中在波节,但无长 距离的能量传播
15 – 6 驻 波 第十五章 机械波 四 驻波的能量 2 k d ( ) t y W 2 p d ( ) x y W 驻波的能量在相邻的波腹和波节间往复变化, 在相邻的波节间发生动能和势能间的转换,动能 主要集中在波腹,势能主要集中在波节,但无长 距离的能量传播. A B C 波 节 波 腹 x x 位移最大时 平衡位置时
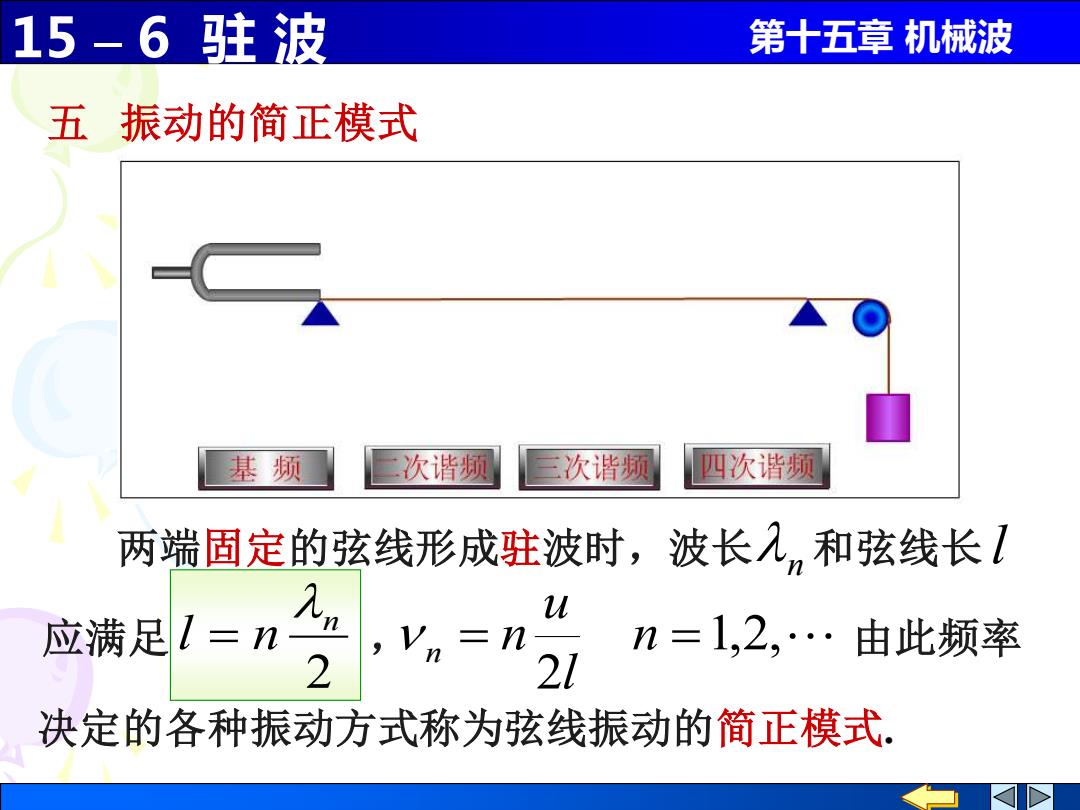
15-6驻波 第十五章机械波 五振动的简正模式 基频 次谐频 三次谐频 四次谐频 两端固定的弦线形成驻波时,波长人,和弦线长1 威满=, Vn=n 7 n=1,2,·由此频率 决定的各种振动方式称为弦线振动的简正模式
15 – 6 驻 波 第十五章 机械波 五 振动的简正模式 应满足 , 由此频率 两端固定的弦线形成驻波时,波长 和弦线长 2 n l n = 1,2, 2 = n = l u n n n l 决定的各种振动方式称为弦线振动的简正模式
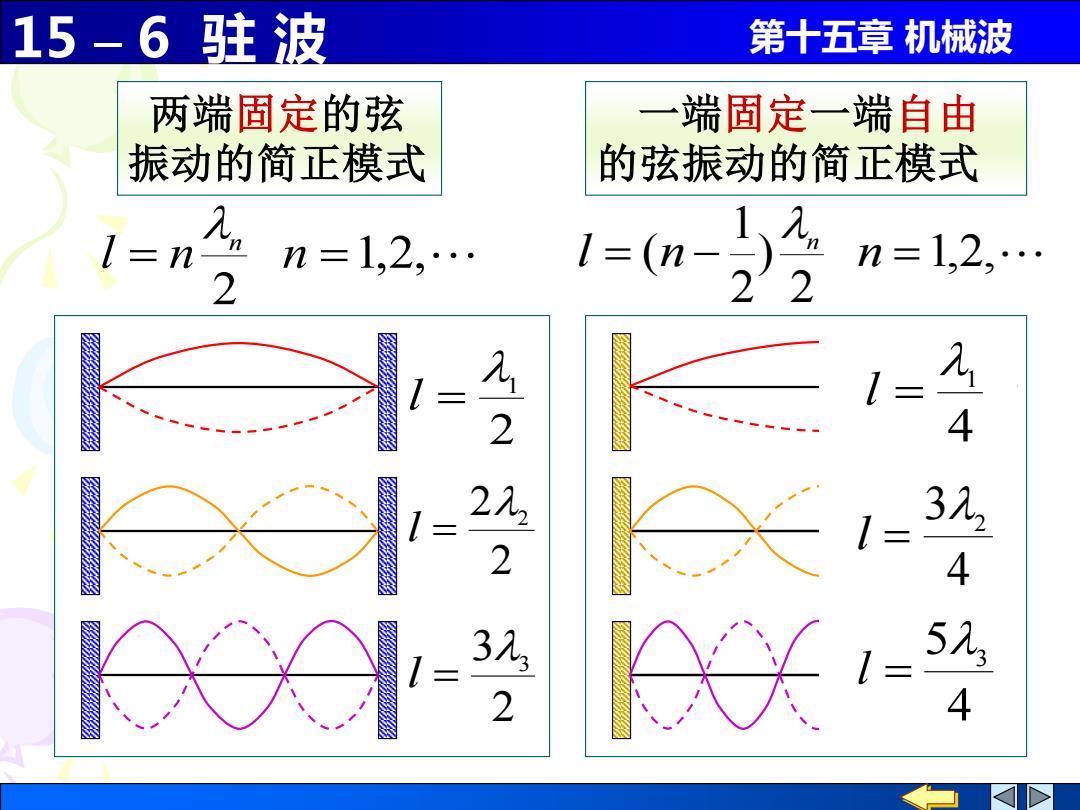
15-6驻波 第十五章机械波 两端固定的弦 端固定一端自由 振动的简正模式 的弦振动的简正模式 l=n- m n=1,2,. 1 l=(n- n=1,2, 2 22 22 1= 4 22 2 4 52 2 4
15 – 6 驻 波 第十五章 机械波 1,2, 2 l = n n = n 两端固定的弦 振动的简正模式 一端固定一端自由 的弦振动的简正模式 1,2, 2 ) 2 1 l = (n − n = n 2 1 l = 2 22 l = 2 33 l = 4 1 l = 4 32 l = 4 53 l =