高等教育出版社：《物理学教程》教材电子教案（PPT课件，马文蔚第四版）第十四章 机械振动 14-6 简谐运动的合成

14-6简谐运动的合成 第十四章机械振动 两个同方向同频率简谐运动的合成 这4o以t x=x+X2 x=Acos(at+o) X2 x Xx A=V4+45+2A4cos(p2-p) A sin +42 sin p2 两个同方向同频 tan o 率简谐运动合成 4 coso+42 cosz 后仍为简谐运动

14 – 6 简谐运动的合成 第十四章 机械振动 1 A1  1 x x 0 一 两个同方向同频率简谐运动的合成 1 2 x = x + x 1 1 2 2 1 1 2 2 cos cos sin sin tan      A A A A + + = 2 cos( ) 1 2 2 1 2 2 2 A = A1 + A + A A  − x = Acos(t +) cos( ) 1 = 1  +1 x A t cos( ) 2 = 2  +2 x A t   A  x2 x A2   2 两个同方向同频 率简谐运动合成 后仍为简谐运动

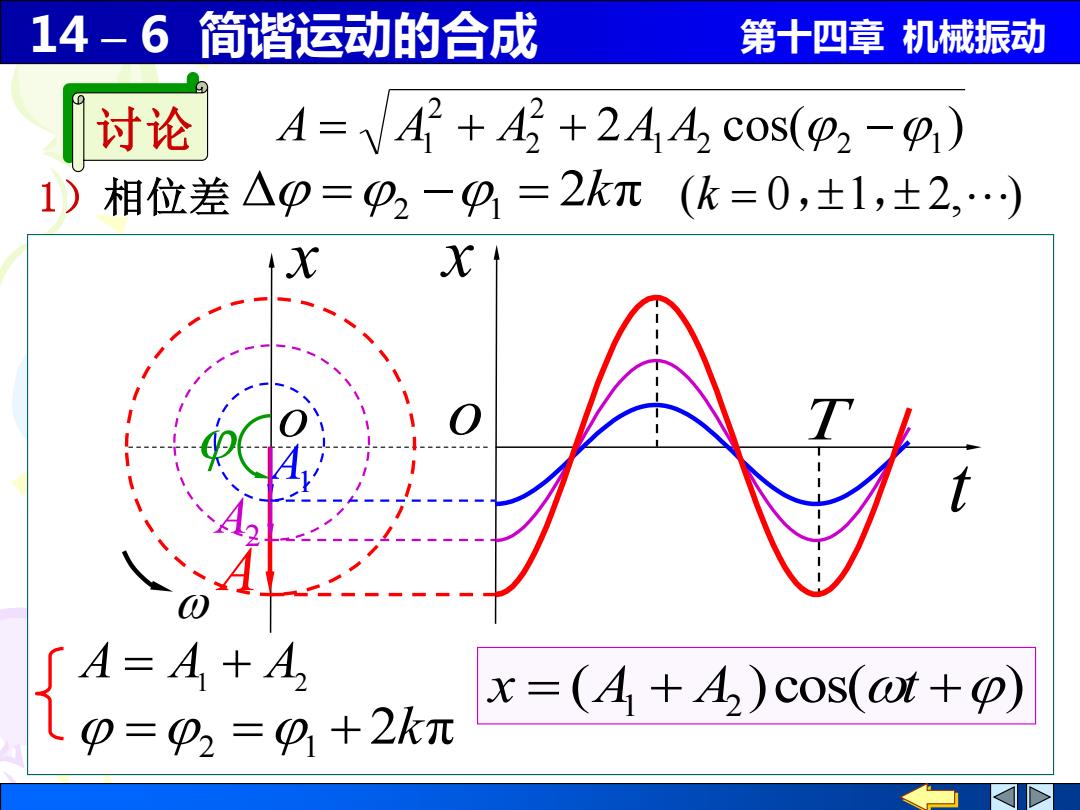
14-6简谐运动的合成 第十四章机械振动 讨论 A=A2+2+244 cos(22-) 1) 相位差△p=P2-91=2kπ(k=0,±1，±2，…) X ∫A=A+A x=(A+4)cos(at+) p=p2=9,+2k元

14 – 6 简谐运动的合成 第十四章 机械振动 x x t o o  =2 =1 + 2kπ ( )cos( ) x = A1 + A2 t + A A = A1 + A2  A1 A2 T 1）相位差  =2 −1 = 2kπ (k = 0，1， 2, ) 2 cos( ) 1 2 2 1 2 2 2 讨论 A = A1 + A + A A  −

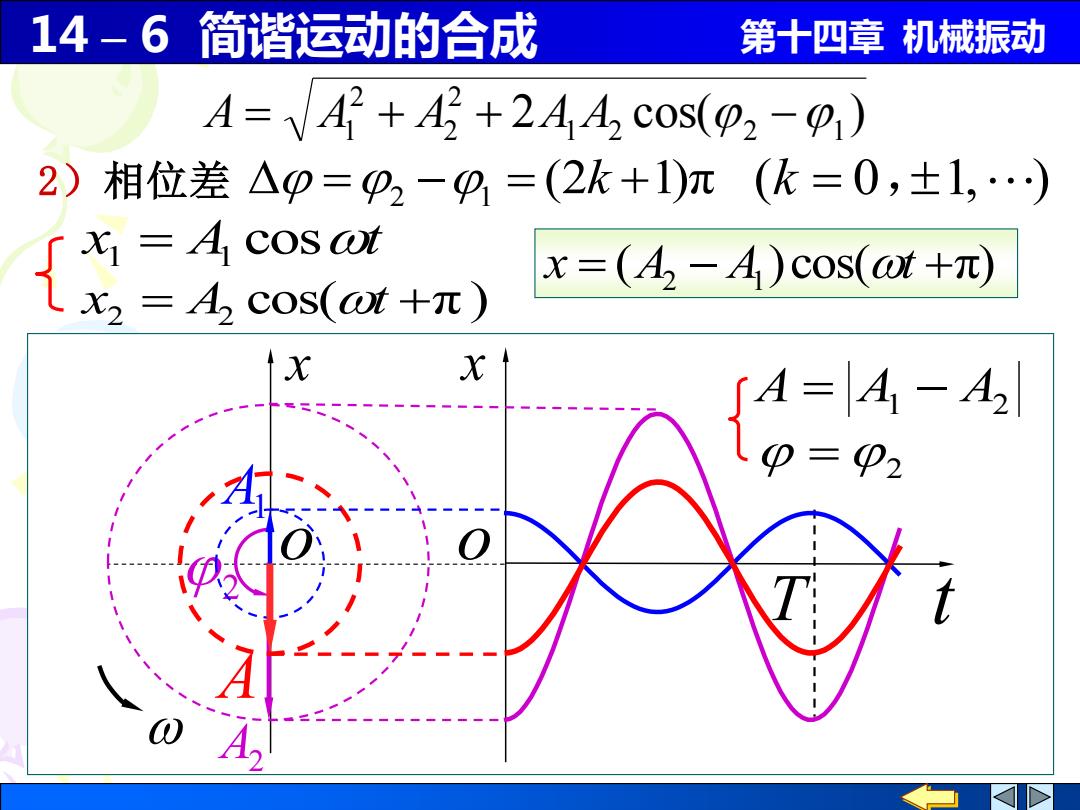
14-6简谐运动的合成 第十四章机械振动 A=42+42+244 cos(2-) 2)相位差△p=92-91=(2k+1)m(k=0,±1，) x=A cosot X2=A,cos(ot+π) x=(A,2-A)cos(@t+π) x X ∫A=A1-A2

14 – 6 简谐运动的合成 第十四章 机械振动 x x t o o A = A1 − A2  =  2 ( )cos( π) x = A2 − A1 t +  2 cos( ) 1 2 2 1 2 2 2 A = A1 + A + A A  − T A2  2 A1 A 2）相位差  =2 −1 = (2k +1)π (k = 0，1, ) x A cost 1 = 1 cos( π ) x2 = A2 t +

14-6简谐运动的合成 第十四章机械振动 1)相位差P2-9=2k (k=0,±1，…) A=4+A 相互加强 2)相位差p2-9=(2k+1)元(k=0,±1，…) A=4-4 相互削弱 3)一般情况 A+A>A>4-4

14 – 6 简谐运动的合成 第十四章 机械振动 3）一般情况 A1 + A2  A  A1 − A2 A = A1 − A2 2）相位差 1）相位差 A = A1 + A2 2 −1 = 2kπ (k = 0，1，) 相互加强 相互削弱 2 −1 = (2k +1)π (k = 0，1，)

14-6简谐运动的合成 第十四章机械振动 二多个同方向同频率简谐运动的合成 x=A cos(at+) x2 =A2 cos(@t+p2) xn=Ar cos(aot+e) X=X1+X2+…+xm X x=Acos(at+o) 多个同方向同频率简谐运动合成仍为简谐运动

14 – 6 简谐运动的合成 第十四章 机械振动 1 A1  x o 二 多个同方向同频率简谐运动的合成 A2   2 A3  3  x = Acos(t +) n x = x + x ++ x 1 2  cos( ) 1 = 1  +1 x A t cos( ) 2 = 2  +2 x A t cos( ) n n n x = A t + A   多个同方向同频率简谐运动合成仍为简谐运动

14-6简谐运动的合成 第十四章机械振动 X=A cosot A x2=Acos(ot+△p) x3=Acos(t+2△p) AAA A Ax A=A=NA, xy=4 cos[axt+(N-1)A] 1)△p=2元 Γ△0 论 (k=0,±1，±2，) 2)V△⑩=2k'元 (k'≠W,k'=±1，±2，) 、△0 W个矢量依次相接构 成一个闭合的多边形 A=0

14 – 6 简谐运动的合成 第十四章 机械振动 A1  A2  A3  A4  o x A5        A A NA0 i =  i = A   x A cost 1 = 0 cos( ) x2 = A0 t +  cos[ ( 1) ] xN = A0 t + N −  cos( 2 ) x3 = A0 t +  A1  A2  A3  A4  x O A5  A6  A = 0 (k' kN,k' = 1,2, ) 2） N = 2k'π 1）  = 2kπ (k = 0,1,2, ) 个矢量依次相接构 成一个闭合的多边形 . N 讨 论

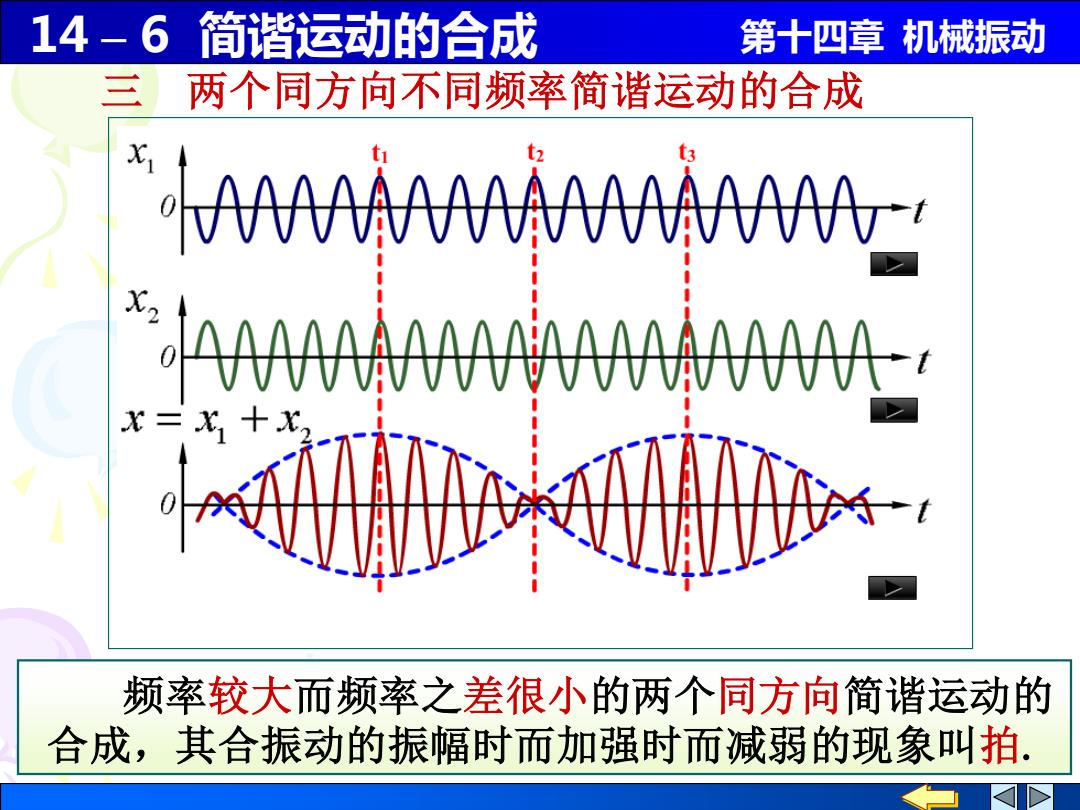
14-6简谐运动的合成 第十四章机械振动 两个同方向不同频率简谐运动的合成 AAAAAAAAAAAAA AAAAAAAAAA- 频率较大而频率之差很小的两个同方向简谐运动的 合成，其合振动的振幅时而加强时而减弱的现象叫拍

14 – 6 简谐运动的合成 第十四章 机械振动 三 两个同方向不同频率简谐运动的合成 频率较大而频率之差很小的两个同方向简谐运动的 合成，其合振动的振幅时而加强时而减弱的现象叫拍

14-6简谐运动的合成 第十四章机械振动 「x1=Ac0sot=Ac0s2πyt x=x+x2 x2=A cos@t=4 cos 2n v2t 讨论A=A2,V2-y<y+V2的情况 方法一 x=x1+x2=Ac0s2元yt+A2C0S2πV,t x=(24c0s2πY0cos2m V2+ 2 2 振幅部分 合振动频率

14 – 6 简谐运动的合成 第十四章 机械振动 振幅部分 合振动频率 x x x A t A t 1 2 1 1 2 2π 2 = + = cos2π + cos  讨论 A1 = A2  2 − 1  1 + 2 , 的情况 x A t t 2 ) cos 2π 2 (2 cos 2π 2 1 2 1 1  −  + = x A t A t 1 1 1 1 2π 1 = cos = cos  x A t A t 2 2 2 2 2π 2 = cos = cos  1 2 x = x + x 方法一

14-6简谐运动的合成 第十四章机械振动 x=(2A,C0S2 tV2-vt)cos2n 2 振幅部分 合振动频率 振动频率V=(y1+V2)/2 =2A 振幅 .=0 2元π-业T=元 2 V2- V=V-V 拍频（振幅变化的频率）

14 – 6 简谐运动的合成 第十四章 机械振动 π 2 2π 2 1 = − T   2 1 1  − T = A A t 2 2 cos 2π 2 1 1  − =  = 2 − 1  = ( 1 + 2 ) 2 A max = 2A1 Amin = 0 振幅部分 合振动频率 x A t t 2 ) cos 2π 2 (2 cos 2π 2 1 2 1 1  −  + = 振幅 振动频率 拍频（振幅变化的频率）

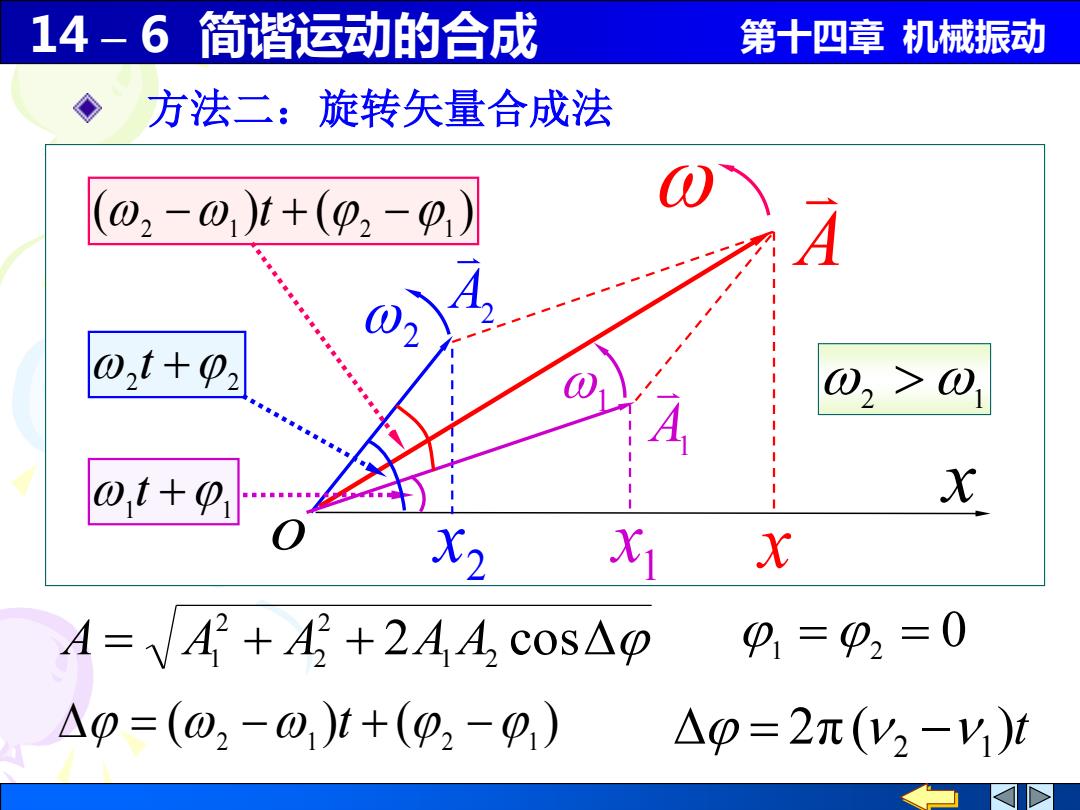
14-6简谐运动的合成 第十四章机械振动 方法二：旋转矢量合成法 (02-01)t+（p2- 1 A 0,t+p2 @2 >0 0t+p1 X X. X1 A=VA+A+2AA,c0S△p P=p2=0 △0=(02-0，)t+(02-9) △p=2π(y2-y1)i

14 – 6 简谐运动的合成 第十四章 机械振动 x o = + + 2 1 2 cos 2 2 2 A A1 A A A ( ) ( )  = 2 −1 + 2 −1 t A2  2 x 2 x  A  A1  1 x 1 1 +1 t ( ) ( ) 2 −1 +  2 −1 t 2 +2 t 方法二：旋转矢量合成法 2 1 1 = 2 = 0 2π ( )t  =  2 −1