高等教育出版社：《物理学教程》教材电子教案（PPT课件，马文蔚第四版）第九章 静电场中的导体与电介质 9-5 静电场的能量和能量密度

9-5静电场的能量能量密度 第九章静电场中的导体和电介质 电容器的电能 dw =Udg q dq C 1 20 C= dq W= QU=-cu2 电容器贮存的电能W。= =00=cw

9 – 5 静电场的能量 能量密度 第九章静电场中的导体和电介质 + + + + + + + + + - - - - - - - - - E  C Q 2 2 = 一 电容器的电能 q C q dW =Udq = d 2 2 e 2 1 2 1 2 QU CU C Q 电容器贮存的电能 W = = =  = Q q q C W 0 d 1 2 2 1 2 1 W = QU = CU U dq + U Q C =

9-5静电场的能量能量密度 第九章静电场中的导体和电介质 二 静电场的能量 能量密度 1 aS 2 2 电场能量密度 W。=aE2=ED 2 2 物理意义 电场是一种物质，它具有能量 电场空间所存储的能量 形.=Jwdr=7E2dw

9 – 5 静电场的能量 能量密度 第九章静电场中的导体和电介质 二 静电场的能量 能量密度 2 e 2 1 W = CU 物理意义 电场是一种物质，它具有能量. 电场空间所存储的能量   = = V V W w V E dV 2 1 d 2 e e  电场能量密度 w E ED 2 1 2 1 2 e =  = 2 ( ) 2 1 Ed d S = E Sd 2 2 1 = 

9-5静电场的能量能量密度 第九章静电场中的导体和电介质 例1如图所示，球形电容器的内、外半径分别为R 和R，所带电荷为士Q.若在两球壳间充以电容率为 的电介质，问此电容器贮存的电场能量为多少？ 解E= 19 4πer2 1 We= 2 32元28r4 dW。=w.dV= 8元8

9 – 5 静电场的能量 能量密度 第九章静电场中的导体和电介质 R1 R2 例1 如图所示,球形电容器的内、外半径分别为 和 ，所带电荷为 ．若在两球壳间充以电容率为 的电介质，问此电容器贮存的电场能量为多少？ R2 R1  Q  解 2 r 4π 1 e r Q E    = r dr 2 4 2 2 e 2 32π 1 r Q w E  =  = r r Q W w V d 8π d d 2 2 e e  = = ) 1 1 ( 8π d 8π d 1 2 2 R R 2 2 e e 2 1 R R Q r Q r W = W = = −    

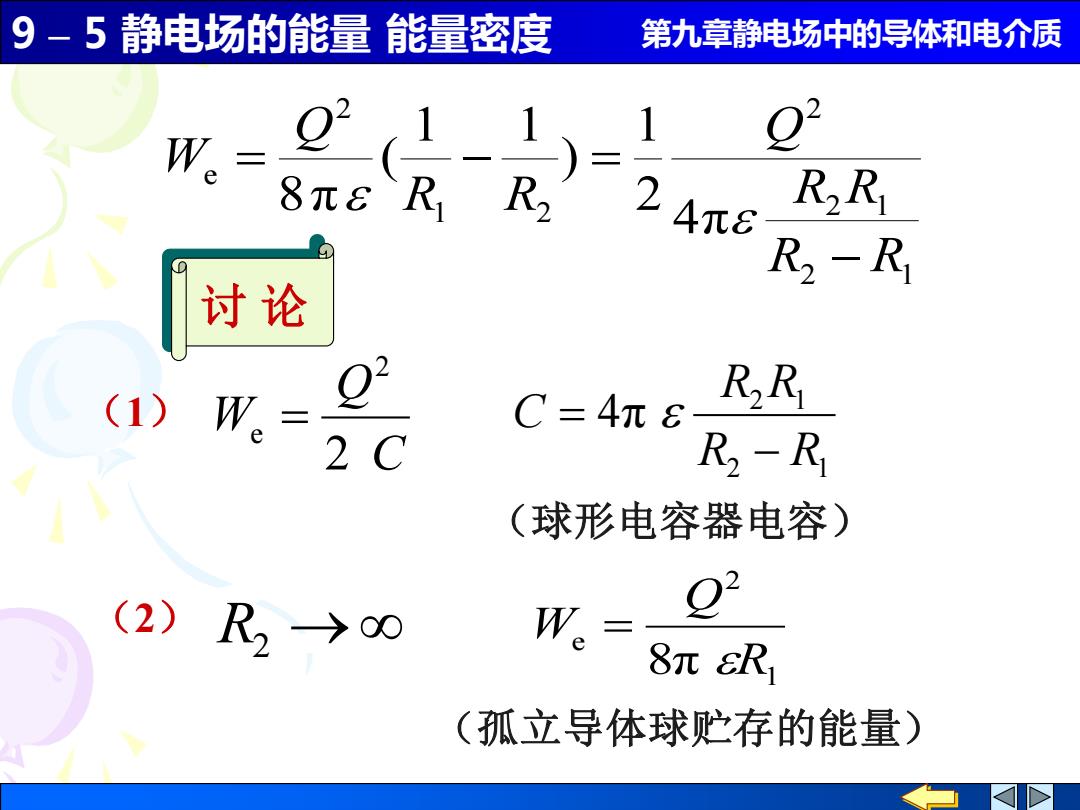
9-5静电场的能量能量密度 第九章静电场中的导体和电介质 22 8元eRR-24πe RR R-R 讨论 (1) W。= 02 RR C=4π6 2 c R-R (球形电容器电容) (2)R2→00 W。= 02 8πR (孤立导体球贮存的能量)

9 – 5 静电场的能量 能量密度 第九章静电场中的导体和电介质 2 1 2 1 2 1 2 2 e 4π 2 1 ) 1 1 ( 8π R R R R Q R R Q W − = − =   C Q W 2 2 e = 2 1 2 1 4π R R R R C − =  （球形电容器电容） 讨 论 R2 → 1 2 e 8π R Q W  = （1） （2） （孤立导体球贮存的能量）

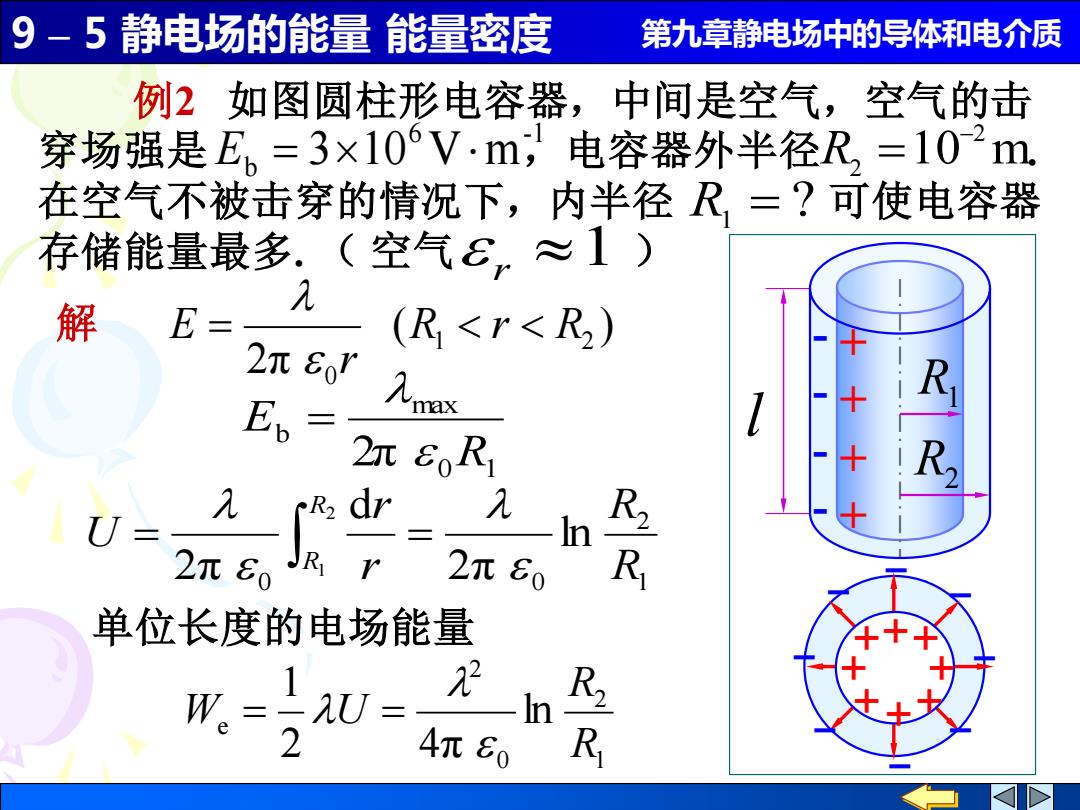
9-5静电场的能量能量密度 第九章静电场中的导体和电介质 例2如图圆柱形电容器，中间是空气，空气的击 穿场强是E,=3×106V·m,电容器外半径R=102m. 在空气不被击穿的情况下，内半径R,=?可使电容器 存储能量最多.（空气8，≈1） 解 E= (R<r<R2) 2T80r Ep= 2元60R1 cR dr U= R2 2元60JR r 2元E0 R 单位长度的电场能量 n 22 2 4元80 R

9 – 5 静电场的能量 能量密度 第九章静电场中的导体和电介质 ( ) 2π 1 2 0 R r R r E =     0 1 max b 2π R E   = 1 2 0 0 ln 2π d 2π 2 1 R R r r U R R     = =  解  r 1 例2 如图圆柱形电容器，中间是空气，空气的击 穿场强是 ，电容器外半径 . 在空气不被击穿的情况下，内半径 可使电容器 存储能量最多. 6 -1 Eb = 310 Vm 10 m 2 2 − R = ? R1 = （ 空气 ） 1 2 0 2 e ln 2 4π 1 R R W U   =  = 单位长度的电场能量 l + + + + - - - - R1 R2 ++ + + + + ++ _ _ _ _ _ _ _ _

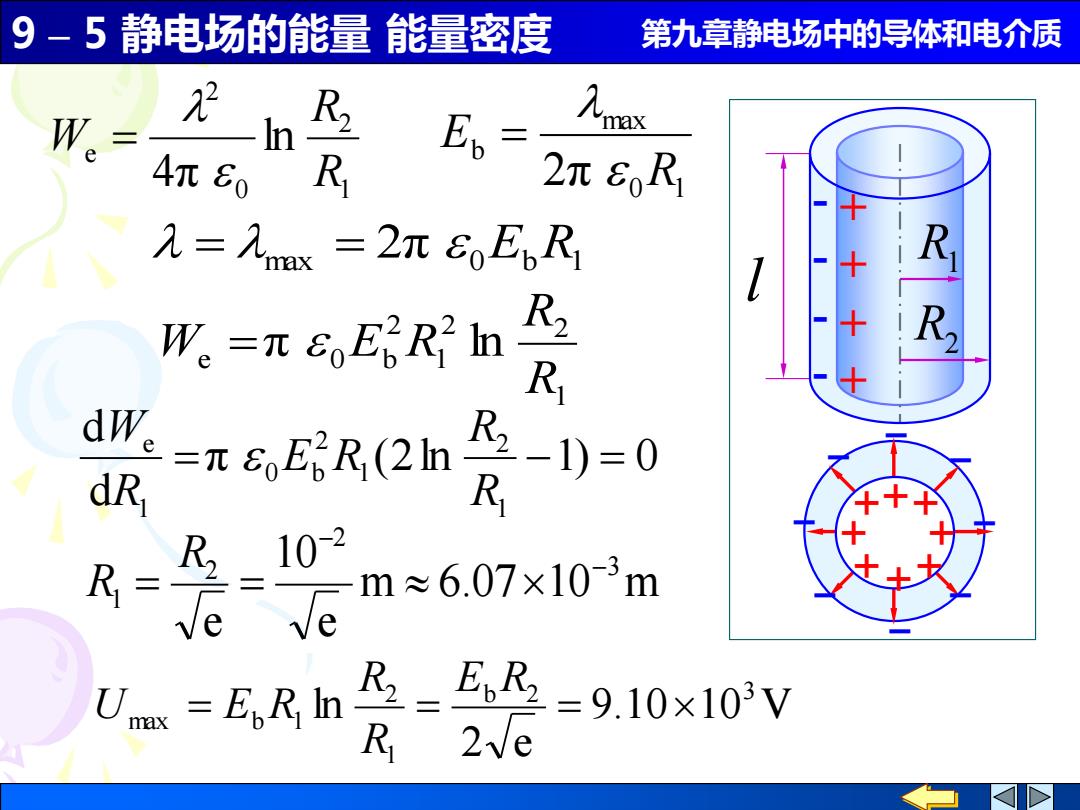
9-5静电场的能量能量密度 第九章静电场中的导体和电介质 W。= R2 Ep= 人may 4π60R 2元6R, 九=九ax=2元6EbR We=πEE2R2n R R dWe dR =πER(2n -1)=0 R 10-2 R= R m≈6.07×10-3m ve e max =EpR In 2=9.10×103V R 2ve

9 – 5 静电场的能量 能量密度 第九章静电场中的导体和电介质 max 2π 0 Eb R1  =  =  1 2 2 1 2 e 0 b π ln R R W =  E R π (2ln 1) 0 d d 1 2 1 2 0 b 1 e = − = R R E R R W  m 6.07 10 m e 10 e 3 2 2 1 − − = =   R R 0 1 max b 2π R E   = 1 2 0 2 e ln 4π R R W   = l + + + + - - - - R1 R2 ++ + + + + ++ _ _ _ _ _ _ _ _ 9.10 10 V 2 e ln b 2 3 1 2 max = b 1 = =  E R R R U E R