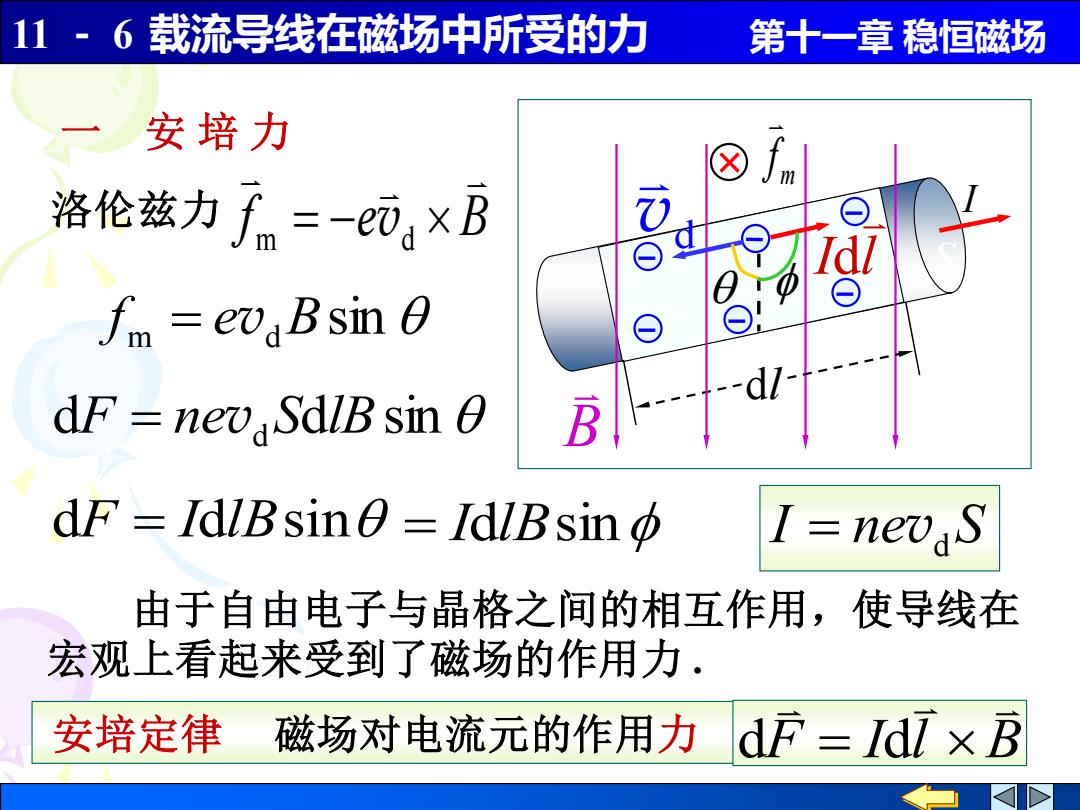
11·6载流导线在磁场中所受的力 第十一章稳恒磁场 一安培力 洛伦兹力fm=-⑦×B f=evaBsin 0 dF nev SdlB sin 0 dF IdlBsin IdlBsin I=nevaS 由于自由电子与晶格之间的相互作用,使导线在 宏观上看起来受到了磁场的作用力. 安培定律 磁场对电流元的作用力d疗=Idi×B
11 - 6 载流导线在磁场中所受的力 第十一章 稳恒磁场 dl I S B 一 安 培 力 洛伦兹力 f e B = − m d v f m = evd Bsin dF = nevd SdlBsin = IdlBsin I = nevd S 由于自由电子与晶格之间的相互作用,使导线在 宏观上看起来受到了磁场的作用力 . 安培定律 磁场对电流元的作用力 F I l B d = d m f vd dF = IdlBsin I l d

11 ,6载流导线在滋场中所受的力 第十一章稳恒磁场 安培定律 dF=Idi×B dF IdlB sin o 意义磁场对电流元作用的力,在数值上等 于电流元Id1的大小、电流元所在处的磁感强度B 大小以及电流元和磁感应强度之间的夹角少的正弦 之乘积,dF垂直于Idi和B所组成的平面,且dF 与Idi×B同向. 有限长载流导线 所受的安培力 Idl F=∫dF=∫d×B B
11 - 6 载流导线在磁场中所受的力 第十一章 稳恒磁场 B I l d F d 有限长载流导线 所受的安培力 F F I l B l l = d = d F I l B 安培定律 d = d dF = IdlBsin 意义 磁场对电流元作用的力 ,在数值上等 于电流元 的大小 、电流元所在处的磁感强度 大小以及电流元和磁感应强度之间的夹角 的正弦 之乘积 , 垂直于 和 所组成的平面, 且 与 同向 . I l d B I l d B F d F d I l B d I l d B F d

11·6载流导线在磁场中所受的力 第十一章稳恒磁场 例1如图一通有电流I的闭合回路放在磁感应强 度为B的均匀磁场中,回路平面与磁感强度B垂直. 回路由直导线AB和半径为P的圆弧导线BCA组成, 电流为顺时针方向,求磁场作用于闭合导线的力, 解E=-IABB X B d 根据对称性分析 F2x=0 F2=F2y F:=JdF2,dF,sin 0 X X
11 - 6 载流导线在磁场中所受的力 第十一章 稳恒磁场 B A C x y I 0 0 B o 根据对称性分析 F F j y 2 = 2 0 F2x = F I ABBj 解 1 = − 2 d 2 d 2 sin F = F y = F F1 dF2 r I l d dF2 I l d 例 1 如图一通有电流 的闭合回路放在磁感应强 度为 的均匀磁场中,回路平面与磁感强度 垂直 . 回路由直导线 AB 和半径为 的圆弧导线 BCA 组成 , 电流为顺时针方向, 求磁场作用于闭合导线的力. I B r B

11~6载流导线在磁场中所受的力 第十一章稳恒磁场 F,=∫df,=∫d,sn6 =∫BIdl sin O 因dl=rdO 店=0s6d0 F,BI(2rcos0)j=BI ABj 由于F=-BIABi 故F=F+F=0
11 - 6 载流导线在磁场中所受的力 第十一章 稳恒磁场 A C x y r I F1 I l d 0 B dF2 I l d o 0 B 2 d 2 d 2 sin F = F y = F = BIdlsin − = 0 0 π 2 sin d F BIr F BI r j BI ABj 2 = (2 cos0 ) = d 因 dl = rd F BI ABj 由于 1 = − 0 F = F1 + F2 = 故
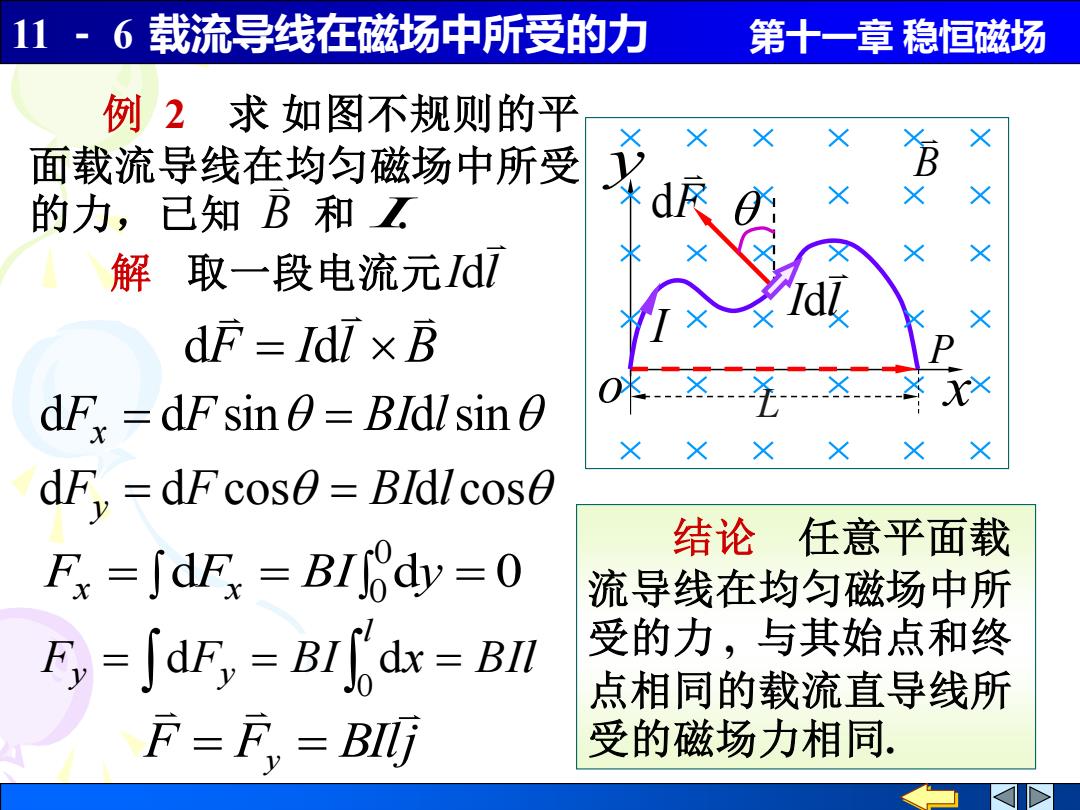
11·6载流导线在磁场中所受的力 第十一章稳恒磁场 例2求如图不规则的平 面载流导线在均匀磁场中所受 的力,已知B和Z d尽 解取一段电流元Idl dF Idl x B dF,=dFsin BIdlsin dF,dF cos0 BIdl cos 结论任意平面载 F=∫dF=BI6dy=0 流导线在均匀磁场中所 F,=∫dE,=BIdr=Bl 受的力,与其始点和终 点相同的载流直导线所 F-F=BILj 受的磁场力相同
11 - 6 载流导线在磁场中所受的力 第十一章 稳恒磁场 P x y o I B L F d d d 0 0 0 Fx = Fx = BI y = F F BIlj y = = F F BI x BIl l y = y = = 0 d d F I l B d = d dFx = dFsin = BIdlsin 解 取一段电流元 I l d dFy = dF cos = BIdl cos 结论 任意平面载 流导线在均匀磁场中所 受的力 , 与其始点和终 点相同的载流直导线所 受的磁场力相同. 例 2 求 如图不规则的平 面载流导线在均匀磁场中所受 的力,已知 B 和 . I I l d
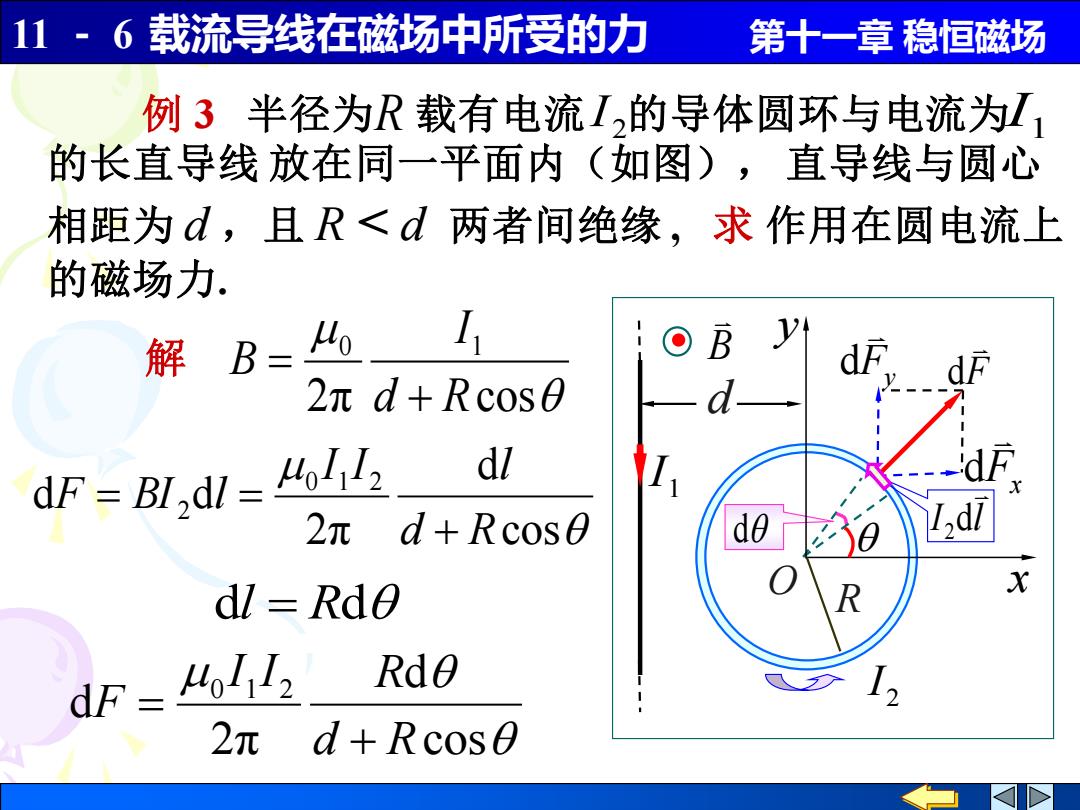
11~6载流导线在磁场中所受的力 第十一章稳恒磁场 例3半径为R载有电流I,的导体圆环与电流为, 的长直导线放在同一平面内(如图),直导线与圆心 相距为d,且R<d两者间绝缘,求作用在圆电流上 的磁场力. 解B= 40 B 2元d+Rcos0 dF=Bl,dl=o dl 2π dl Rd0 dF= 4I1I2 Rde 2π
11 - 6 载流导线在磁场中所受的力 第十一章 稳恒磁场 x y O 2 I 1 I d R 例 3 半径为 载有电流 的导体圆环与电流为 的长直导线 放在同一平面内(如图), 直导线与圆心 相距为 d ,且 R < d 两者间绝缘 , 求 作用在圆电流上 的磁场力. 1 I 2 R I 解 2π cos 0 1 d R I B + = cos d 2π d d 0 1 2 2 d R I I l F BI l + = = dl = Rd cos d 2π d 0 1 2 d R I I R F + = F Fy d d Fx d I l d2 . B d

11·6载流导线在磁场中所受的力 第十一章稳恒磁场 dFs=dFcoso= Rcosae 2元d+Rcos0 dFy =dF sin =o Rsin ade 2元 d Rcos0 F=LolilzR cos@de d 2π d+Rcos0 d =4,1112(1- d2-R2 4I12R sin ado =0 2π d+Rcos0
11 - 6 载流导线在磁场中所受的力 第十一章 稳恒磁场 cos sin d 2π d d sin 0 1 2 d R I I R Fy F + = = cos cos d 2π d d cos 0 1 2 d R I I R Fx F + = = x y F Fy d d Fx d O 2 I 1 I d I l d2 R d (1 ) 2 2 0 1 2 d R d I I − = − + = 2π 0 0 1 2 cos cos d 2π d R I I R Fx 0 cos sin d 2π 2π 0 0 1 2 = + = d R I I R Fy . B
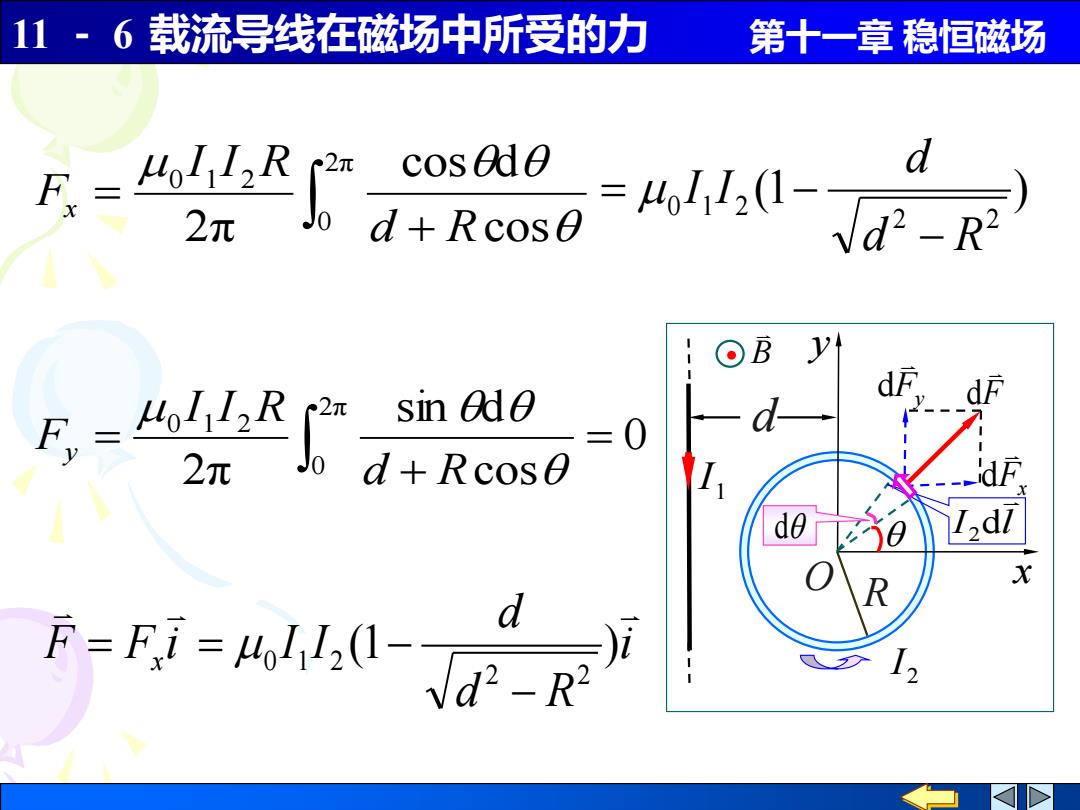
11~6载流导线在磁场中所受的力 第十一章稳恒磁场 F=Lol R cosade a 2元 d Rcose =,--R OB 2π sin ade =0 2元 d+Rcose F=Fi=412--R d )i
11 - 6 载流导线在磁场中所受的力 第十一章 稳恒磁场 i d R d F F i I I x (1 ) 2 2 0 1 2 − = = − (1 ) 2 2 0 1 2 d R d I I − = − + = 2π 0 0 1 2 cos cos d 2π d R I I R Fx 0 cos sin d 2π 2π 0 0 1 2 = + = d R I I R Fy x y F Fy d d Fx d O 2 I 1 I d I l 2 d R d . B

11·6载流导线在磁场中所受的力 第十一章稳恒磁场 二电流的单位两无限长平行载流直导线间的相互作用 B 41 2πd B.= 412 πd dF2 =B 12dl2 sin /B, dF, 中=90°,sinb=1 d5-Bl,d,=4lld业 2πd dF _dF 41I2 dl, d 2πd dg=Bl,d山=l4dl 2πd
11 - 6 载流导线在磁场中所受的力 第十一章 稳恒磁场 1 I 2 I d 二 电流的单位 两无限长平行载流直导线间的相互作用 d I B 2π 0 1 1 = d I B 2π 0 2 2 = dF2 = B1 I 2 dl 2 sin d I I l F B I l 2π d d d 0 2 1 1 1 2 1 1 = = d I I l F l F d 2π d d d 0 1 2 1 1 2 2 = = = 90 ,sin =1 d I I l F B I l 2π d d d 0 1 2 2 2 1 2 2 = = B1 B2 dF2 2 2 I dl 1 d 1 I l dF1

11~6载流导线在磁场中所受的力 第十一章稳恒磁场 国际单位制中电流单位安培的定义 在真空中两平行长直导线相 距1m,通有大小相等、方向相 同的电流,当两导线每单位长度 上的吸引力为2×10-7Nm1时, B 规定这时的电流为1A(安培). d d 可得4=4π×10-7N·A2 =4元×10-7H.m1 d近-d= 412 问若两直导线电流方向相反 dl,dl, 2πd 二者之间的作用力如何?
11 - 6 载流导线在磁场中所受的力 第十一章 稳恒磁场 国际单位制中电流单位安培的定义 在真空中两平行长直导线相 距 1 m ,通有大小相等、方向相 同的电流,当两导线每单位长度 上的吸引力为 时, 规定这时的电流为 1 A (安培). 7 1 2 10 N m − − 7 1 4π 10 H m − − = 问 若两直导线电流方向相反 d 二者之间的作用力如何? I I l F l F d 2π d d d 0 1 2 2 2 1 1 = = 1 I 2 I B1 B2 dF2 dF1 d 7 2 0 4π 10 N A − − 可得 =