
8 -8 电场强度与电势梯度 第八章静电场 等势面(电势图示法) 空间电势相等的点连接起来所形成的面称为等势 面.为了描述空间电势的分布,规定任意两相邻等势 面间的电势差相等 在静电场中,电荷沿等势面移动时,电场力做功 Wa6=9(W。-Va)=qE.d7-0 在静电场中,电场强度E总是与等势面垂直的, 即电场线是和等势面正交的曲线簇. W6=f心goE.di=0 E⊥dl qo≠0E≠0di≠0
8 – 8 电场强度与电势梯度 第八章静电场 空间电势相等的点连接起来所形成的面称为等势 面. 为了描述空间电势的分布,规定任意两相邻等势 面间的电势差相等. 一 等势面(电势图示法) 在静电场中,电荷沿等势面移动时,电场力做功 ( ) d 0 0 0 b a ab a b W q V V q E l 0 d 0 b a ab W q E l q0 0 E 0 dl 0 E l d E 在静电场中,电场强度 总是与等势面垂直的, 即电场线是和等势面正交的曲线簇
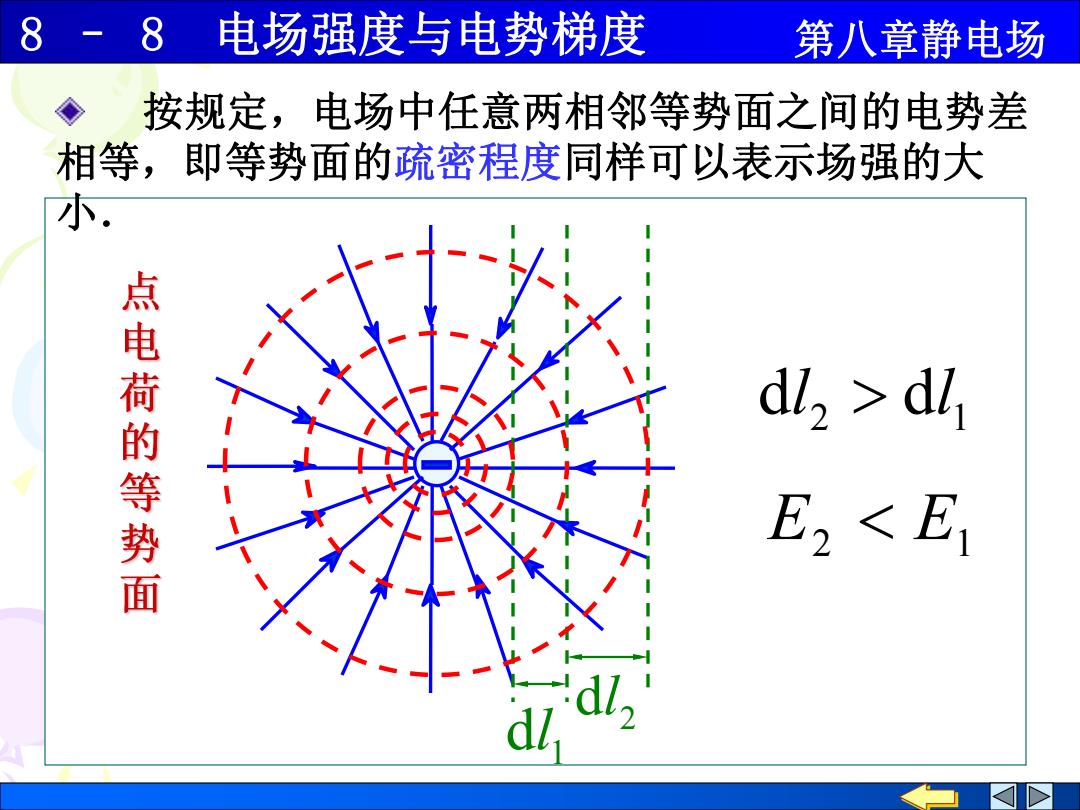
8 -8电场强度与电势梯度 第八章静电场 ◆ 按规定,电场中任意两相邻等势面之间的电势差 相等,即等势面的疏密程度同样可以表示场强的大 小. 点电荷的等势面 dl,dl E2<E1
8 – 8 电场强度与电势梯度 第八章静电场 d 1 l 2 dl d 2 d 1 l l E2 E1 按规定,电场中任意两相邻等势面之间的电势差 相等,即等势面的疏密程度同样可以表示场强的大 小.
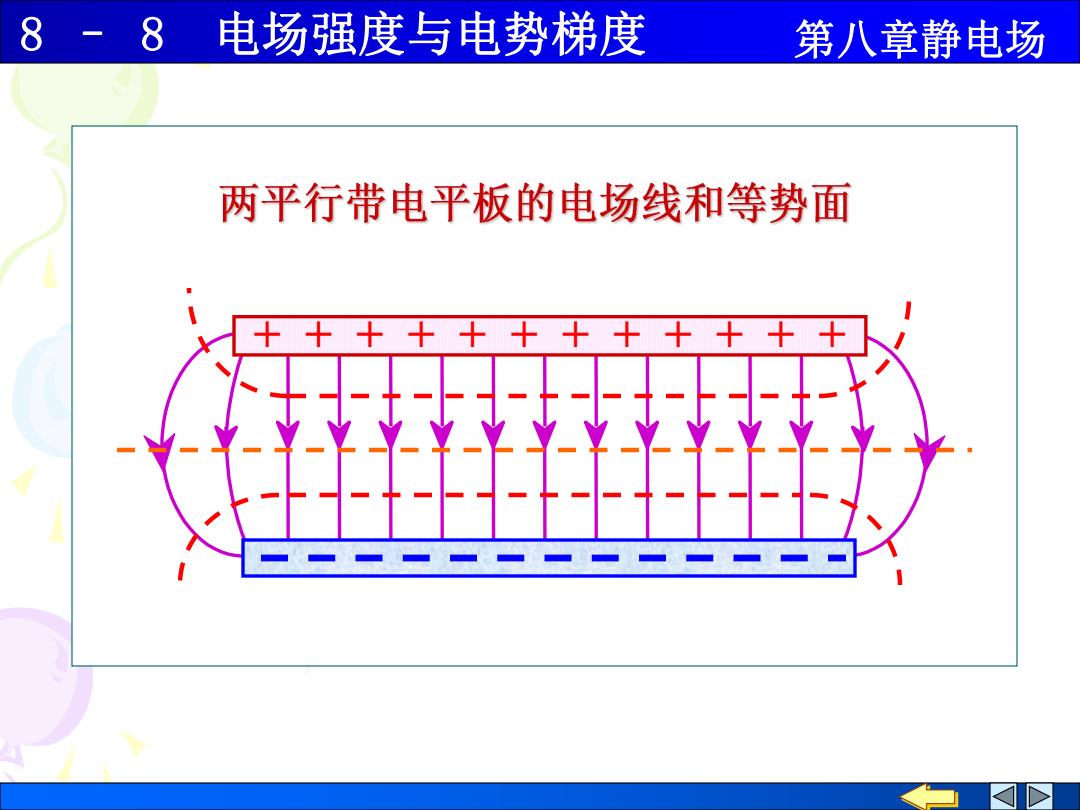
8- 8电场强度与电势梯度 第八章静电场 两平行带电平板的电场线和等势面
8 – 8 电场强度与电势梯度 第八章静电场 + + + + + + + + + + + +

8 -8电场强度与电势梯度 第八章静电场 一对等量异号点电荷的电场线和等势面
8 – 8 电场强度与电势梯度 第八章静电场 +

8 8 电场强度与电势梯度 第八章静电场 二 电场强度与电势梯度 UB=-(VB-V4)=E·△7 =E△lcos0 E cos0=E △V E -△V=E,△l,E,= △l △V dy E,=-lim V+△V △1→0 dl 电场中某一点的电场强度沿某一方向的分量,等于 这一点的电势沿该方向单位长度上电势变化率的负值
8 – 8 电场强度与电势梯度 第八章静电场 二 电场强度与电势梯度 E l cos U V V E l AB B A ( ) E El cos l V V El l El , l V l V E l l d d lim 0 电场中某一点的电场强度沿某一方向的分量,等于 这一点的电势沿该方向单位长度上电势变化率的负值. V V V l E El A B

8 -8 电场强度与电势梯度 第八章静电场 dy dy E,= E二 dl dl, e .dl>dln∴.En>E dl V+△V dl, E d E 大小 dV 高电势 dl. 低电势 方向 与。相反,由高电势处指向低电势处
8 – 8 电场强度与电势梯度 第八章静电场 V V V E l d 高 电 势 低 电 势 n e e n dl 方向 与 相反,由高电势处指向低电势处 n e n d d l V E 大小 n n d d l V E n dl dl En El n n d d e l V E l V El d d

8- 8 电场强度与电势梯度 第八章静电场 物理意义 (1)空间某点电场强度的大小取决于该点领域内 电势/的空间变化率. (2)电场强度的方向恒指向电势降落的方向. ◆ 直角坐标系中 讨论 E=-(9 OV R)=-gradv 8z E=-VV(电势梯度) 为求电场强度 E提供了一种新的途径 利用电场强度叠加原理 求E的三种方法 利用高斯定理 利用电势与电场强度的关系
8 – 8 电场强度与电势梯度 第八章静电场 k V z V j y V i x V E ) grad ( E V (电势梯度) 直角坐标系中 为求电场强度 E 提供了一种新的途径 求 E 的三种方法 利用电场强度叠加原理 利用高斯定理 利用电势与电场强度的关系 物理意义 (1)空间某点电场强度的大小取决于该点领域内 电势 V 的空间变化率. (2)电场强度的方向恒指向电势降落的方向. 讨 论

8-8电场强度与电势梯度 第八章静电场 三 电场线和等势面的关系 1)电场线与等势面处处正交. (等势面上移动电荷,电场力不做功.) 2)等势面密处电场强度大;等势面疏处电场强度小, 讨论 1) 电场弱的地方电势低;电场强的地方电势高吗? 2) V=0 的地方,龙=0吗? 3)龙相等的地方,V一定相等吗?等势面上 定相等吗?
8 – 8 电场强度与电势梯度 第八章静电场 三 电场线和等势面的关系 1)电场线与等势面处处正交. (等势面上移动电荷,电场力不做功.) 2)等势面密处电场强度大;等势面疏处电场强度小. 1)电场弱的地方电势低;电场强的地方电势高吗? 2) 的地方, 吗 ? 3) 相等的地方, 一定相等吗?等势面上 一定相等吗 ? V 0 E 0 V E E 讨论

8 -8 电场强度与电势梯度 第八章静电场 例1求一均匀带电细圆环轴线上任一点的电场强度, 解 E=-VV dg =Adl q 4π6(x2+R2)2 av E E=E= Z 0x a qx 4元6(x2+R2)'2 4π6(x2+R2)32
8 – 8 电场强度与电势梯度 第八章静电场 例1 求一均匀带电细圆环轴线上任一点的电场强度. 解 x q y x z o R r dq dl P E x V E Ex 2 2 1 2 0 4π (x R ) q V 2 2 3 2 0 4π (x R ) qx E V 2 2 1 2 0 4π (x R ) q x

8 -8电场强度与电势梯度 第八章静电场 例2求电偶极子电场中任意一点A的电势和电场强度. 解 V,= 19 4πE0r+ 1 4元E0T V=V.+V= 9r-r+ 4元60rr <<r ∴.r-r≈hc0s0 rr≈r2
8 – 8 电场强度与电势梯度 第八章静电场 例2 求电偶极子电场中任意一点 A的电势和电场强度. q q 0r r r x y 解 A r r r q r r V V V 4π 0 r r 0 r r r0 cos 2 r r r r q V 4π 0 1 r q V 4π 0 1