
6-6循环过程卡诺循环 第六章热力学基础 热机发展简介 1698年萨维利和1705年纽可门先后发明了蒸 汽机,当时蒸汽机的效率极低.1765年瓦特进 行了重大改进,大大提高了效率.人们一直在 为提高热机的效率而努力,从理论上研究热机 效率问题,一方面指明了提高效率的方向, 一方面也推动了热学理论的发展. 各种热机的效率 液体燃料火箭η=48% 柴油机 7=37% 汽油机 7=25% 蒸汽机 7=8%
6 - 6 循环过程 卡诺循环 第六章热力学基础 热机发展简介 1698年萨维利和1705年纽可门先后发明了蒸 汽机 ,当时蒸汽机的效率极低 . 1765年瓦特进 行了重大改进 ,大大提高了效率 . 人们一直在 为提高热机的效率而努力, 从理论上研究热机 效率问题, 一方面指明了提高效率的方向, 另 一方面也推动了热学理论的发展 . 各种热机的效率 液体燃料火箭 柴油机 汽油机 蒸汽机 = 48% = 8% = 37% = 25%
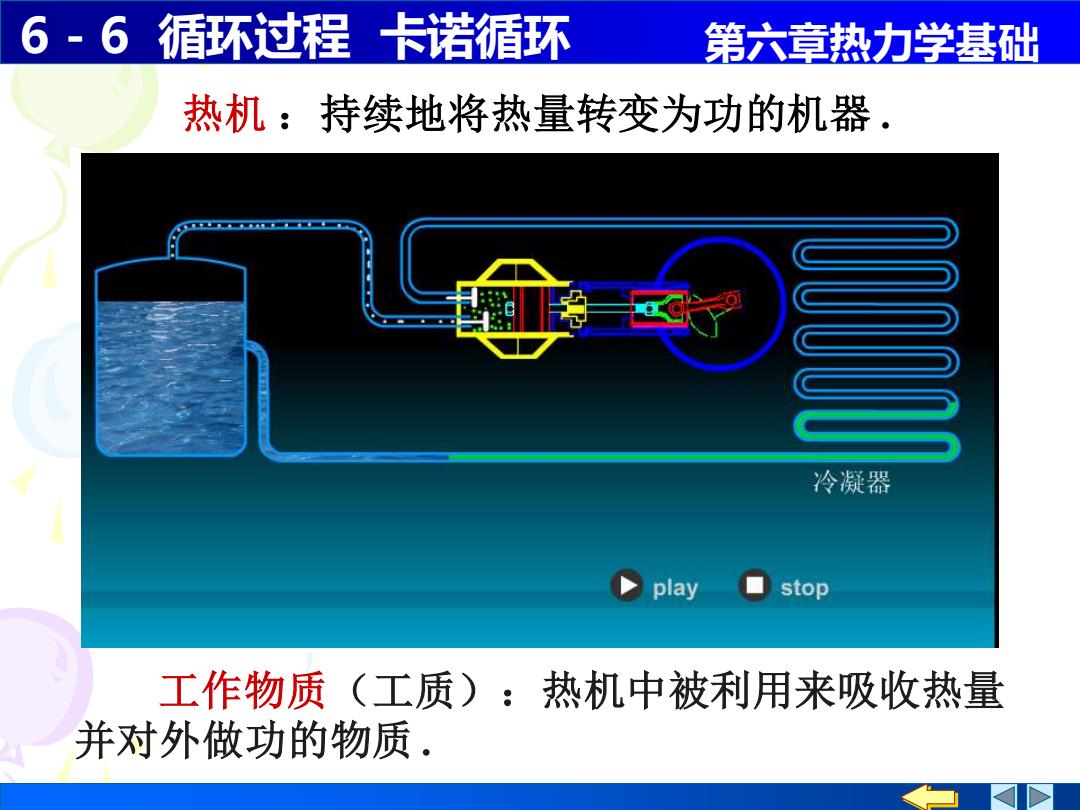
6-6循环过程 卡诺循环 第六章热力学基础 热机:持续地将热量转变为功的机器. 冷凝器 play stop 工作物质(工质): 热机中被利用来吸收热量 并对外做功的物质
6 - 6 循环过程 卡诺循环 第六章热力学基础 热机 :持续地将热量转变为功的机器 . 工作物质(工质):热机中被利用来吸收热量 并对外做功的物质
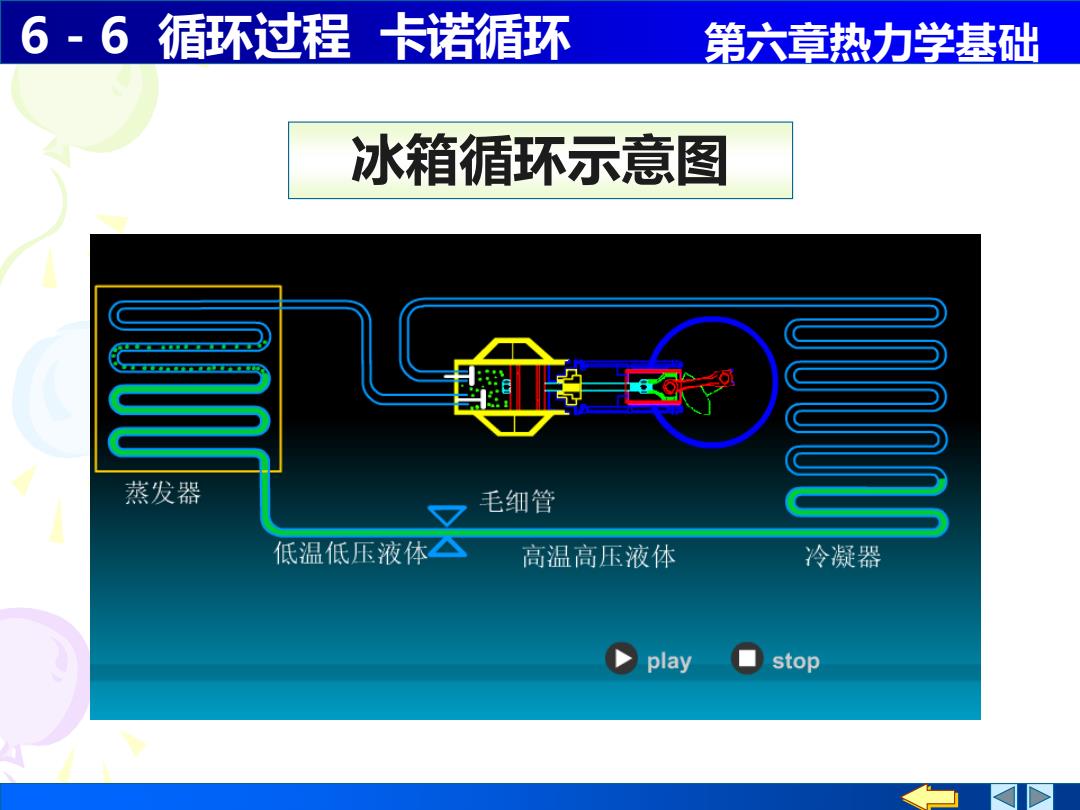
6-6 循环过程卡诺循环 第六章热力学基础 冰箱循环示意图 蒸发器 毛细管 低温低压液体△ 高温高压液体 冷凝器 play ☐stop
6 - 6 循环过程 卡诺循环 第六章热力学基础 冰箱循环示意图
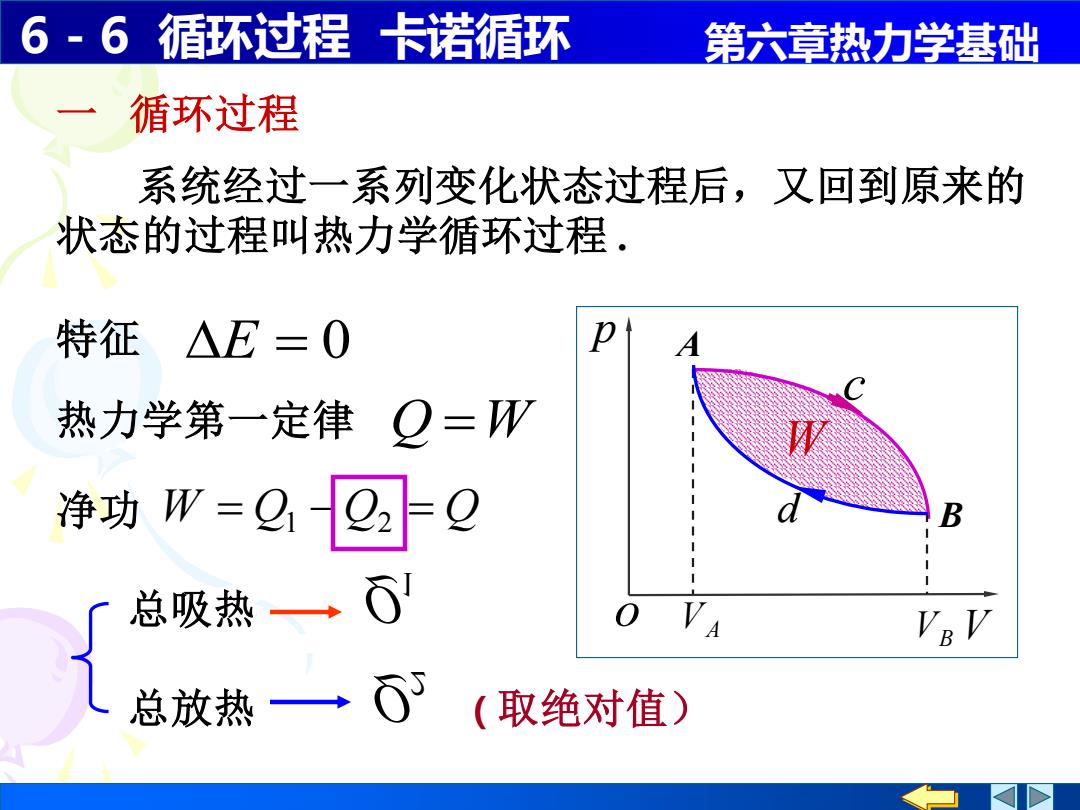
6-6循环过程 卡诺循环 第六章热力学基础 循环过程 系统经过一系列变化状态过程后,又回到原来的 状态的过程叫热力学循环过程 特征△E=0 热力学第一定律 O=W 净功W=QQF0 总吸热 总放热 (取绝对值)
6 - 6 循环过程 卡诺循环 第六章热力学基础 p o V W 系统经过一系列变化状态过程后,又回到原来的 状态的过程叫热力学循环过程 . 热力学第一定律 Q =W Q2 总放热 (取绝对值) 净功 W = Q1 − Q2 = Q 特征 E = 0 一 循环过程 Q1 总吸热 A B VA VB c d
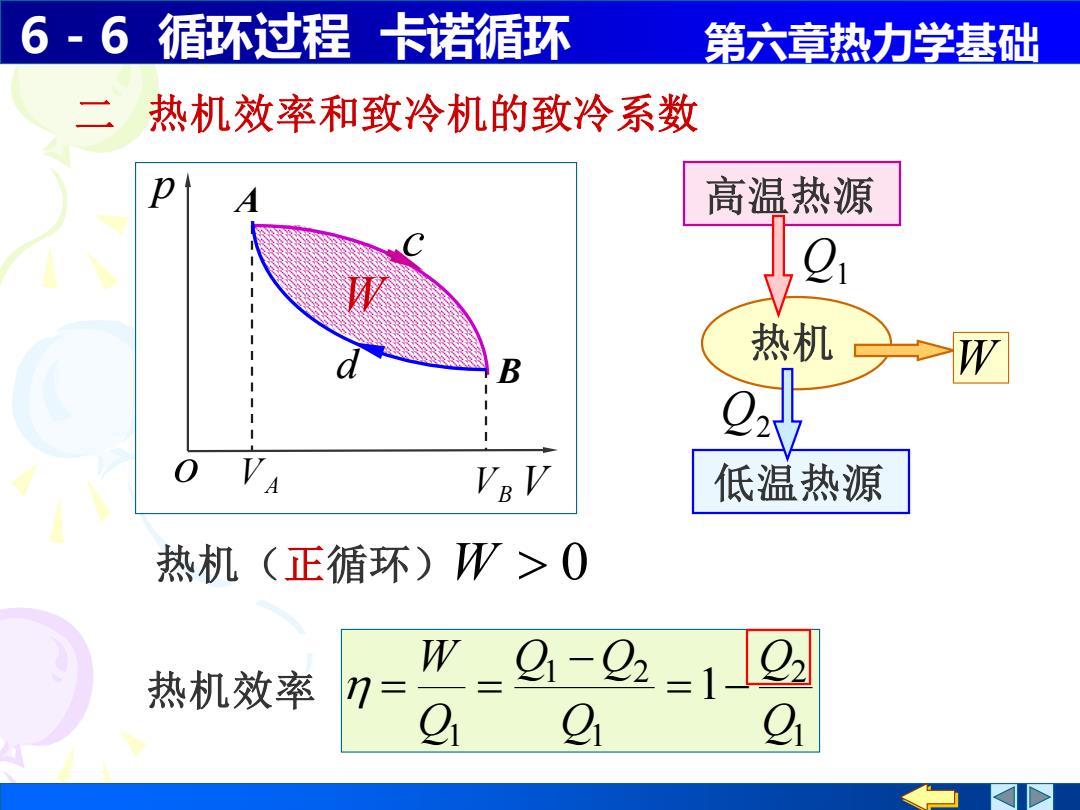
6-6 循环过程卡诺循环 第六章热力学基础 热机效率和致冷机的致冷系数 高温热源 热机 B W VEV 低温热源 热机(正循环)W>O 热机效率 _2-22=12 Q
6 - 6 循环过程 卡诺循环 第六章热力学基础 热机 二 热机效率和致冷机的致冷系数 热机效率 1 2 1 1 2 1 1 Q Q Q Q Q Q W = − − = = 高温热源 低温热源 Q1 热机(正循环) W 0 Q2 W W p o V A B VA VB c d
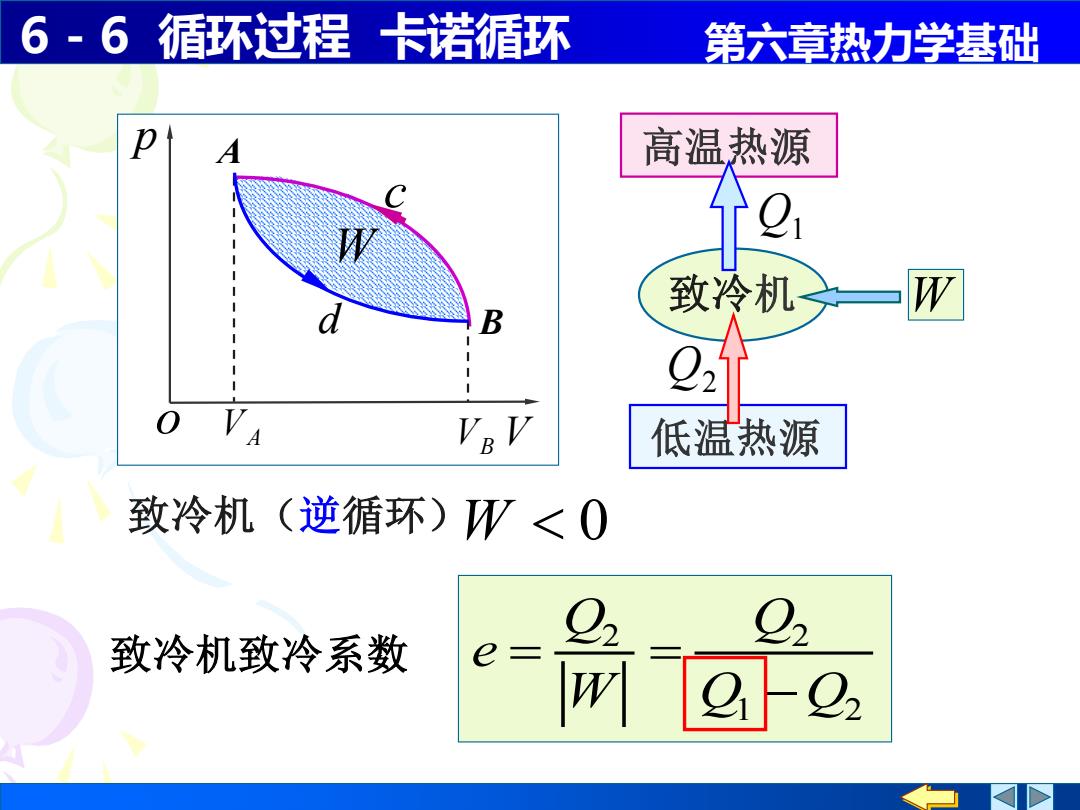
6-6循环过程卡诺循环 第六章热力学基础 高温热源 致冷机— W 031 V。 低温热源 致冷机(逆循环)W<O 致冷机致冷系数
6 - 6 循环过程 卡诺循环 第六章热力学基础 W 致冷机致冷系数 1 2 2 2 Q Q Q W Q e − = = 致冷机(逆循环) W 0 致冷机 高温热源 低温热源 p o V A B VA VB c d Q1 Q2 W

6-6循环过程卡诺循环 第六章热力学基础 例11mol氦气经过如图所示的循环过程,其 中p2=2p1,V4=2%求1-2、2-3、3一4、4-1 各过程中气体吸收的热量和热机的效率. P 解由理想气体物态方程得 P2 2 T2 =2T T3 =4T T4=2T P 212 Cr.m(T2-Ti)=Cr.mTi 41 Q23=Cp.m(T3-7)=2Cp.mTi 234=Cv,m(T4-T3)=-2Cv,mT
6 - 6 循环过程 卡诺循环 第六章热力学基础 1 4 V1 V4 2 3 1 p 2 p P o V Q12 Q34 Q41 Q23 例 1 1 mol 氦气经过如图所示的循环过程,其 中 , 求1—2、2—3、3—4、4—1 各过程中气体吸收的热量和热机的效率 . p2 = 2 p1 V4 = 2V1 解 由理想气体物态方程得 T2 = 2T1 T3 = 4T1 T4 = 2T1 12 ,m 2 1 ,m 1 Q = CV (T −T ) = CV T 23 ,m 3 2 ,m 1 Q = Cp (T −T ) = 2Cp T 34 ,m 4 3 2 ,m 1 Q = CV (T −T ) = − CV T

6-6循环过程卡诺循环 第六章热力学基础 212 =Cy.mT 223 =2Cp.mTi P P2 234=-2Cv,mT QaI=Cp.m(Ti-Ta)=-Cp.mTi Q=Q12+223 CrmT+2CpmT V V4 V Cp.m Cr.m+R W=(p2-p)(W4-V)=p1V1=RT1 91-22=W R了 1(3Cv.m+2R) =15.3%
6 - 6 循环过程 卡诺循环 第六章热力学基础 (3 m 2 ) 1 , 1 T C R RT V + = Q W Q Q Q 1 1 1 2 = − = = 15.3% Cp,m = CV ,m + R ( )( ) 2 1 V4 V1 W = p − p − = p1V1=RT1 Q1 = Q12 + Q23 41 ,m 1 4 ,m 1 Q = Cp (T −T ) = −Cp T = CV ,m T1 + 2Cp,m T1 1 4 V1 V4 2 3 1 p 2 p P o V Q12 Q34 Q41 Q23 Q12 = CV ,m T1 23 ,m 1 Q = 2Cp T Q34 = −2CV ,m T1

6-6 循环过程 卡诺循环 第六章热力学基础 三卡诺循环 1824年法国的年青工程师卡诺提出一个工作 在两热源之间的理想循环一卡诺循环.给出了热机 效率的理论极限值;他还提出了著名的卡诺定理 卡诺循环是由两个准静态等温过程和两个准静 态绝热过程组成. T1>T2 高温热源T1 21 P2 卡诺热机 W 2 V4 V2 V3 低温热源T2
6 - 6 循环过程 卡诺循环 第六章热力学基础 卡诺循环是由两个准静态等温过程和两个准静 态绝热过程组成 . 三 卡诺循环 低温热源 T2 高温热源 T1 卡诺热机 Q1 Q2 W V o p T2 W T1 A B C D p1 p2 4 p p3 V1 V4 V2 V3 T1 T2 1824 年法国的年青工程师卡诺提出一个工作 在两热源之间的理想循环—卡诺循环. 给出了热机 效率的理论极限值; 他还提出了著名的卡诺定理

6-6循环过程卡诺循环 第六章热力学基础 理想气体卡诺循环热机效率的计算 T>T 卡诺循环 P A一B等温膨胀 B一C绝热膨胀 C—D 等温压缩 V D 一A绝热压缩 A一B等温膨胀吸热 RT In
6 - 6 循环过程 卡诺循环 第六章热力学基础 V o p T2 W T1 A B C D 1 p 2 p 4 p 3 p V1 V4 V2 V3 理想气体卡诺循环热机效率的计算 A — B 等温膨胀 B — C 绝热膨胀 C — D 等温压缩 D — A 绝热压缩 1 2 卡诺循环 T T Qab Qcd 1 2 1 1 ln V V RT M m A — B 等温膨胀吸热 Q = Qa b =