6-5理想气体的等温过程和绝热过程 第六章热力学基础 等温过程 特征T=常量 1(p1,V,T) 过程方程 卫V=常量 (p2,'2,T) dE 0 P2 2 热力学第一定律 d≌r=dW=pdV Qr =w =f pdr 恒温热源 m RT D= M V
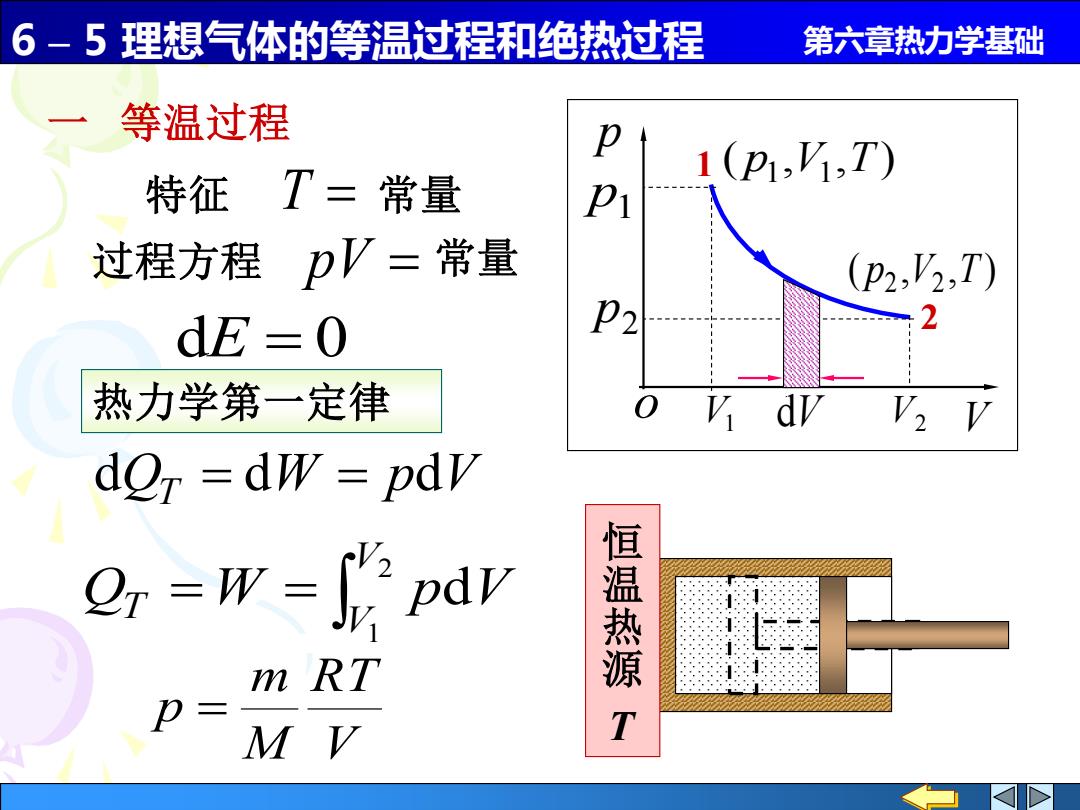
6 – 5 理想气体的等温过程和绝热过程 第六章热力学基础 一 等温过程 热力学第一定律 dE = 0 恒 温 热 源 T V RT M m p = = = 2 1 d V V QT W p V dQT = dW = pdV 1 2 ( , , ) p1 V1 T ( , , ) p2 V2 T p1 p2 V1 V2 p o dV V 特征 T = 常量 过程方程 pV = 常量
6-5理想气体的等温过程和绝热过程 第六章热力学基础 Q红=W= V2 m RT RTIn m RTIn P M M M P2 等温膨胀 等温压缩 1(P1,V1,T) 1(p1,V,T) (P2,',T) (P2,2,T) P2 2 P2 2 V V2 V VV W
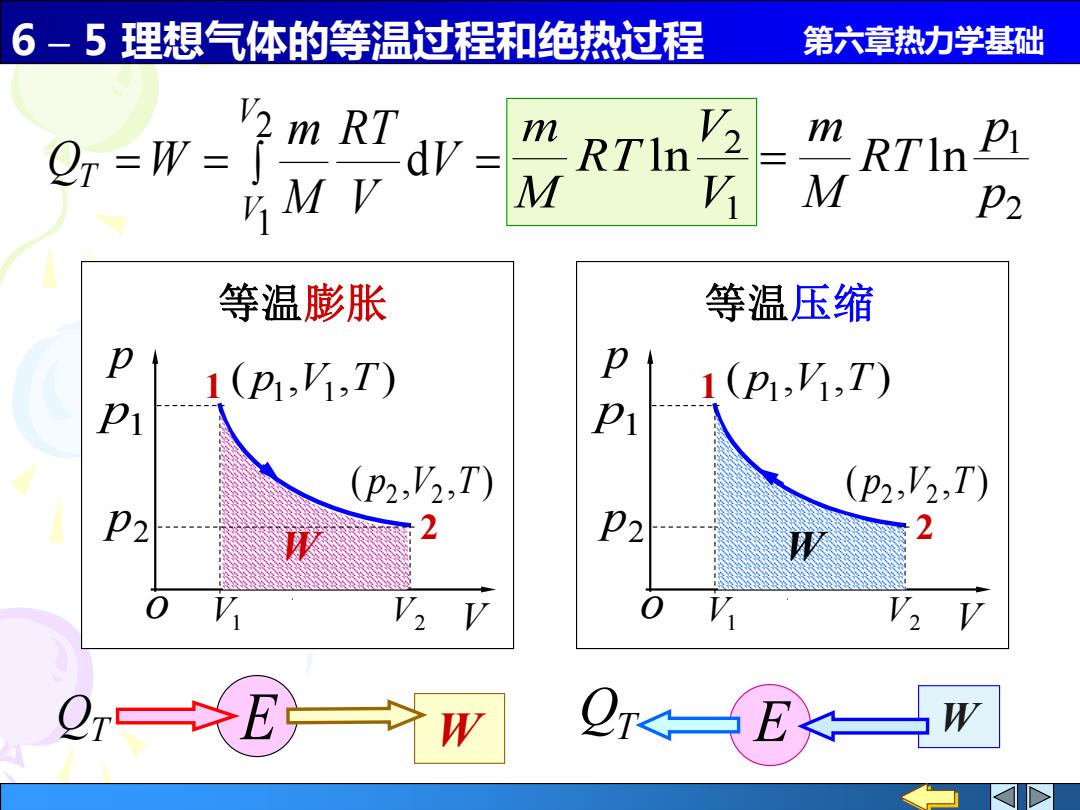
6 – 5 理想气体的等温过程和绝热过程 第六章热力学基础 E E = = V = V R T M m Q W V V T d 2 1 1 2 ln V V RT M m 2 1 ln p p RT M m = 1 2 ( , , ) p1 V1 T ( , , ) p2 V2 T p1 p2 V1 V2 p o V 等温膨胀 W 1 2 ( , , ) p1 V1 T ( , , ) p2 V2 T p1 p2 V1 V2 p o V W 等温压缩 QT W QT W
6-5理想气体的等温过程和绝热过程 第六章热力学基础 二 绝热过程 与外界无热量交换的过程 1(p1,Vi,T1) 特征 do=0 热一律 dw +dE =0 (p2,'2,T2) dw =-dE P2 2 dE= m M Cy.mdT V,V 绝热的汽缸壁和活塞 =-顶Cv.d7 W -
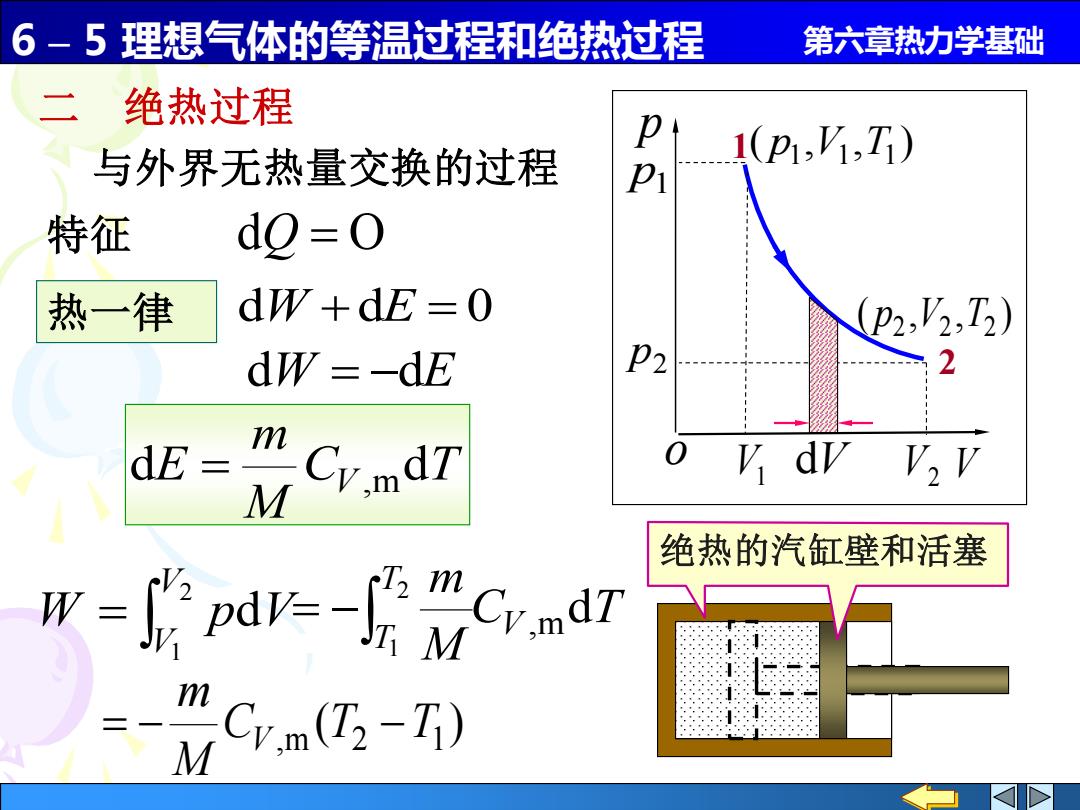
6 – 5 理想气体的等温过程和绝热过程 第六章热力学基础 ( , , ) p1 V1 T1 ( , , ) 2 V2 T2 p 1 2 p1 p2 V1 V2 p V o 二 绝热过程 与外界无热量交换的过程 ( ) C ,m T2 T1 M m = − V − 特征 dQ = O C T M m V T T ,md 2 1 = − C T M m dE = V ,md = 2 1 d V V W p V dV 绝热的汽缸壁和活塞 dW = −dE 热一律 dW +dE = 0
6-5理想气体的等温过程和绝热过程 第六章热力学基础 由热力学第一定律有 1(P1V,T) W=-△E W=- y.m(-乃) P2,V2,T2) M P2 2 若己知p1,1,p2,V2及Y V2 V 从py= R7可得w=C货) R R Cpm-Cvm (p%-p22)lw=p-p2'3 y-1
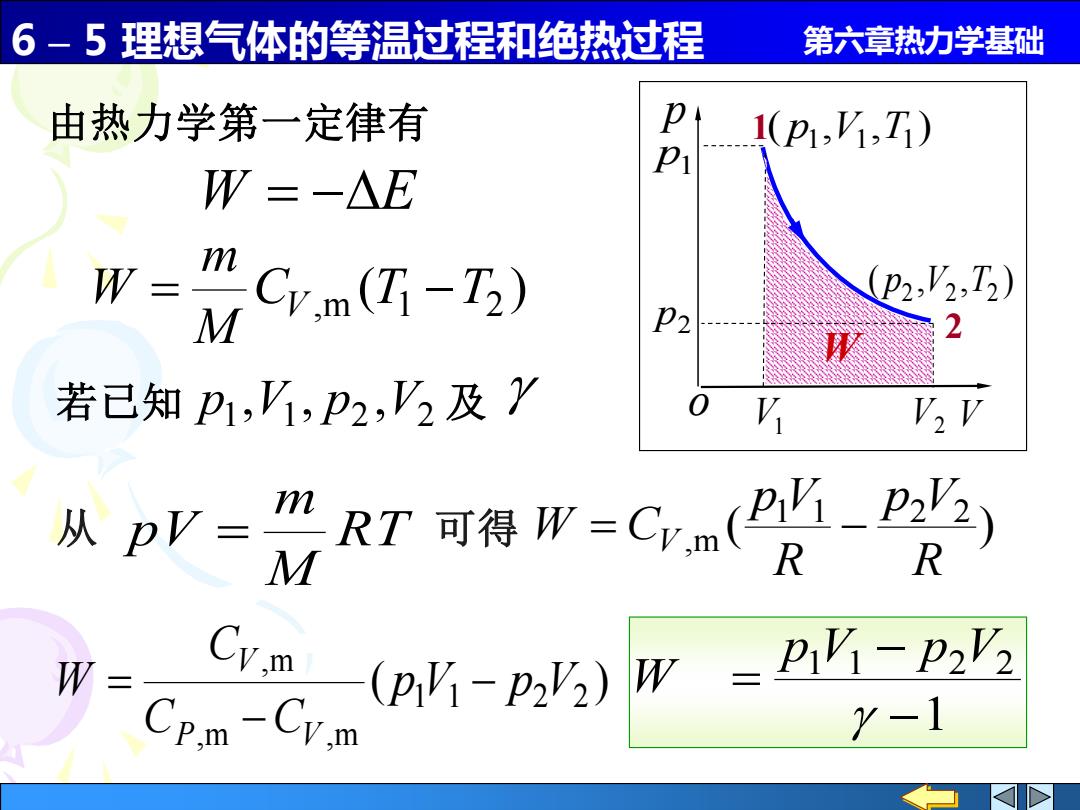
6 – 5 理想气体的等温过程和绝热过程 第六章热力学基础 ( ) 1 1 2 2 ,m ,m ,m p V p V C C C W P V V − − = 1 1 1 2 2 − − = p V p V W ( ) C ,m T1 T2 M m W = V − 若已知 p1 ,V1 , p2 ,V2 及 ( , , ) p1 V1 T1 ( , , ) 2 V2 T2 p 1 2 p1 p2 V1 V2 p o V W W = −E RT M m pV = ( ) 1 1 2 2 ,m R p V R p V 从 可得 W = CV − 由热力学第一定律有
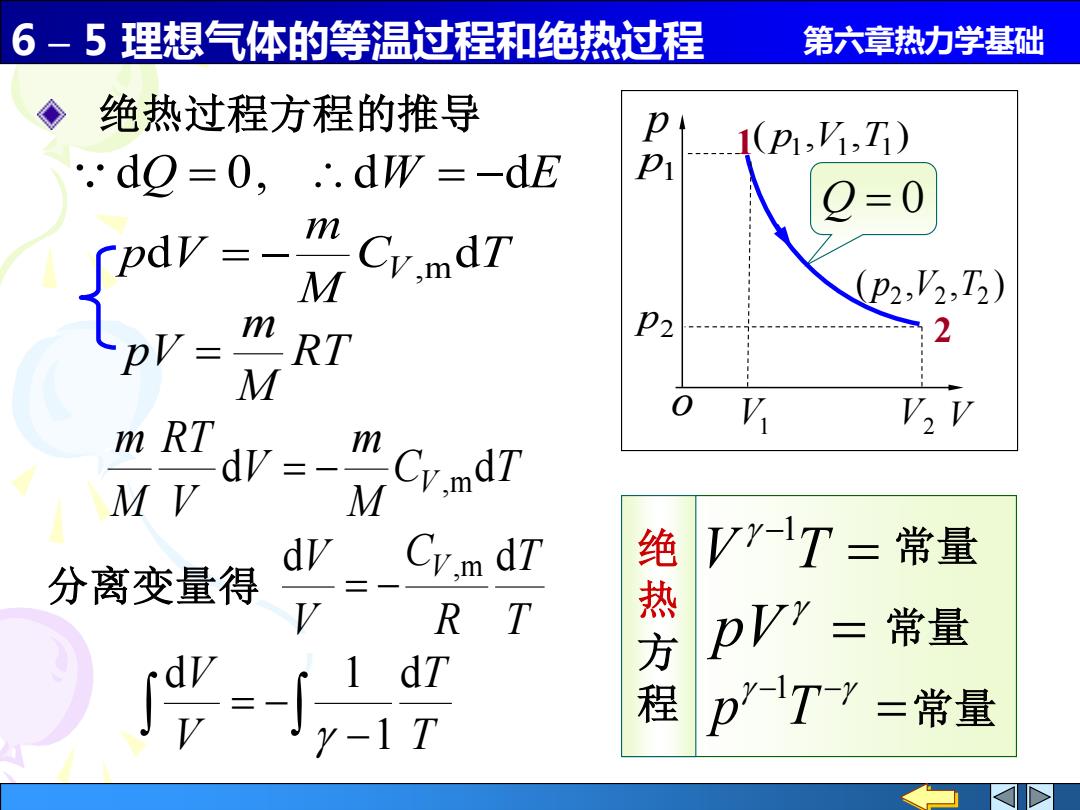
6-5理想气体的等温过程和绝热过程 第六章热力学基础 ◆绝热过程方程的推导 1(P1,,T) ∵dQ=0,∴.dW=-dE =0 Spdv=_ Cv.mdT M (P2,V2,T2) pV= P2 RT 2 M m RT V2 V dV v.mdT M dy Cv.m dT 绝 V”-T=常量 分离变量得 R T 热 pV”=常量 dT 程 r-1 T pTy=常量
6 – 5 理想气体的等温过程和绝热过程 第六章热力学基础 绝热过程方程的推导 dQ = 0, dW = −dE C T M m pdV = − V ,md RT M m pV = C T M m V V RT M m V d md = − , T T V V d 1 d 1 − = − T T R C V dV V ,m d 分离变量得 = − ( , , ) p1 V1 T1 ( , , ) 2 V2 T2 p 1 2 p1 p2 V1 V2 p o V Q = 0 绝 热 方 程 = − V T 1 = pV = − − p T 1 常量 常量 常量

6-5理想气体的等温过程和绝热过程 第六章热力学基础 绝热膨胀 绝热压缩 1(p1,Mi,T) 2(p2,',T2) P2 (p2,',T2) PIY:T) P2 2 V2V VV
6 – 5 理想气体的等温过程和绝热过程 第六章热力学基础 ( , , ) p1 V1 T1 ( , , ) 2 V2 T2 p 1 2 p1 p2 V1 V2 p o V W 绝 热 膨 胀 ( , , ) 1 V1 T1 p ( , , ) 2 V2 T2 p 1 2 p1 p2 V2 V1 p o V W 绝 热 压 缩 E1 E2 E1 E2 W W
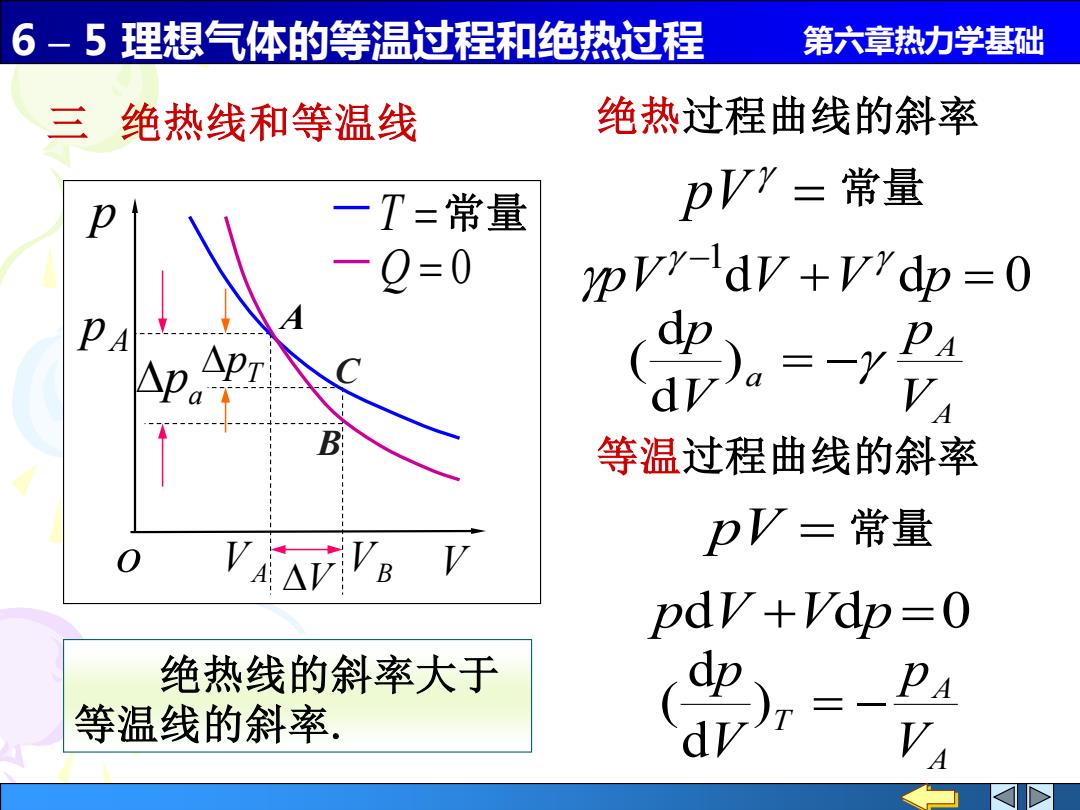
6-5理想气体的等温过程和绝热过程 第六章热力学基础 三绝热线和等温线 绝热过程曲线的斜率 一T=常量 pV”=常量 一 Q=0 nvr-dv+vrdp=0 等温过程曲线的斜率 pV=常量 A△V B pdy+Vdp=0 绝热线的斜率大于 dp PA 等温线的斜率
6 – 5 理想气体的等温过程和绝热过程 第六章热力学基础 三 绝热线和等温线 绝热过程曲线的斜率 等温过程曲线的斜率 pdV +Vdp =0 d d 0 1 + = − pV V V p A A a V p V p ) = − d d ( A A T V p V p ) = − d d ( 绝热线的斜率大于 等温线的斜率. = pV 常量 pV = 常量 A p VA VB A p o V T = Q = 0 V a p T p B C 常量
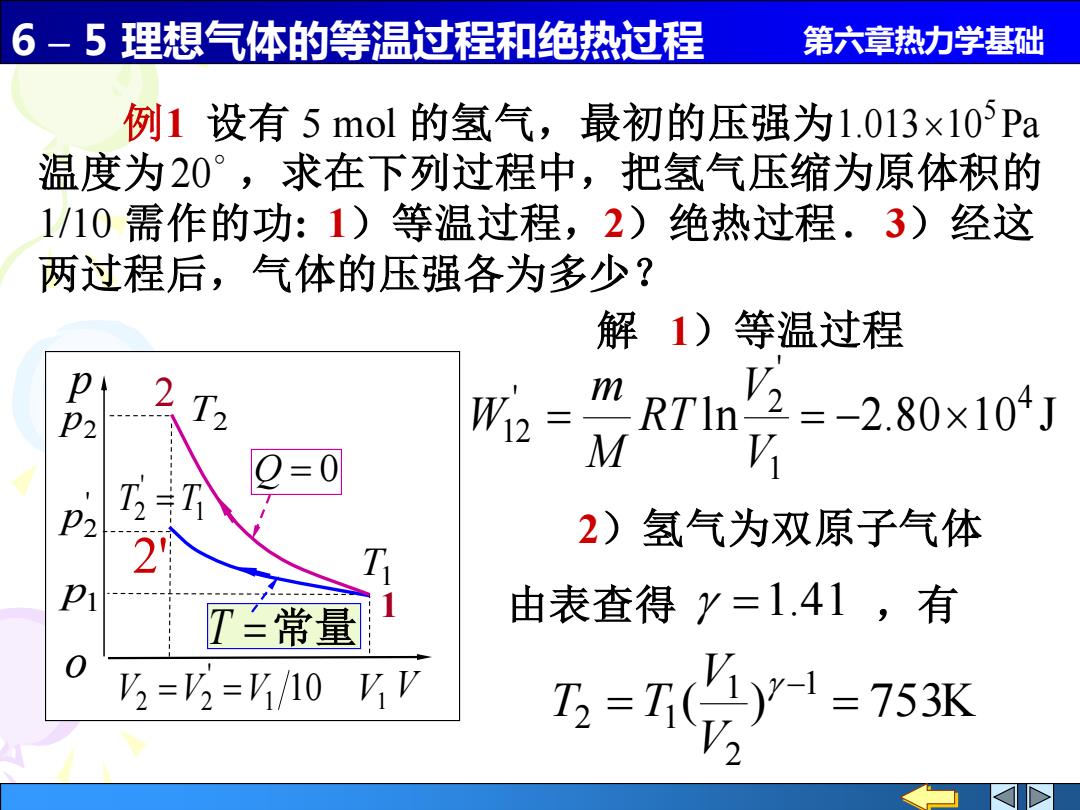
6-5理想气体的等温过程和绝热过程 第六章热力学基础 例1设有5mol的氢气,最初的压强为1.013x105Pa 温度为20°,求在下列过程中,把氢气压缩为原体积的 1/10需作的功:1)等温过程,2)绝热过程.3)经这 两过程后,气体的压强各为多少? 解1)等温过程 p 2 P2 T2 所2 R7n2-280×10] M V P2 2 2)氢气为双原子气体 T二常量 由表查得y=1.41,有 V2=V=V/10 VV 3-7()y1=75K
6 – 5 理想气体的等温过程和绝热过程 第六章热力学基础 例1 设有 5 mol 的氢气,最初的压强为 温度为 ,求在下列过程中,把氢气压缩为原体积的 1/10 需作的功: 1)等温过程,2)绝热过程 . 3)经这 两过程后,气体的压强各为多少? 1.013 10 Pa 5 20 解 1)等温过程 l n 2.8 0 1 0 J 4 1 ' ' 2 12 = = − V V R T M m W 2)氢气为双原子气体 由表查得 =1.41 ,有 ( ) 753K 1 2 1 2 = 1 = − V V T T T1 T2 1 2 p1 p2 V1 10 1 ' V2 =V2 =V p V o ' p2 1 ' T2 = T Q = 0 T = 2' 常量
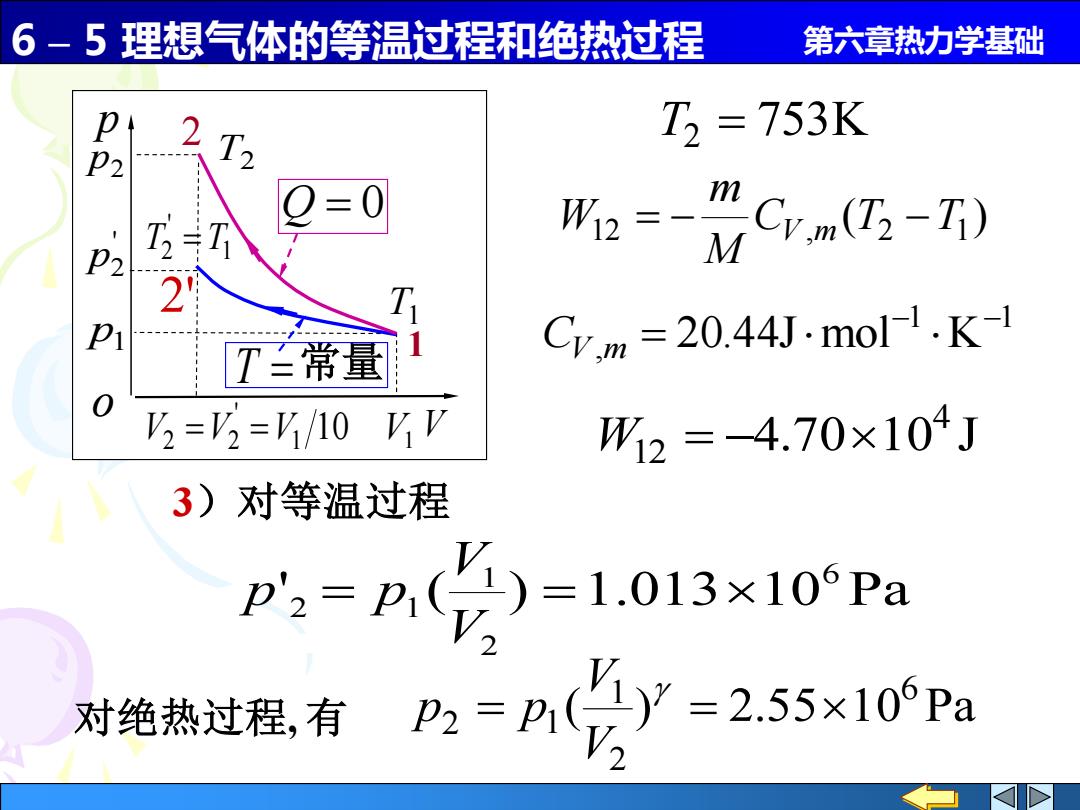
6-5理想气体的等温过程和绝热过程 第六章热力学基础 p 2 T T2=753K 2 P2 Crm④-TD W2=-M 2 T常量 Cvm =20.44J.mol-.K-I V=V,=V/10 VV W2=-4.70×104J 3)对等温过程 P2=,()=1.013x10Pa 对绝热过程,有 P2=Pi(y=2.55x106pa
6 – 5 理想气体的等温过程和绝热过程 第六章热力学基础 T2 = 753K ( ) 12 C , T2 T1 M m W = − V m − 1 1 , 20.44J mol K − − m = CV 4.70 10 J 4 W12 = − 3)对等温过程 ' ( ) 1.013 10 Pa 6 2 1 2 = 1 = V V p p 对绝热过程, 有 ( ) 2.55 10 Pa 6 2 1 2 = 1 = V V p p T1 T2 1 2 p1 p2 V1 10 1 ' V2 =V2 =V p V o ' p2 1 ' T2 = T Q = 0 2' T = 常量

6-5理想气体的等温过程和绝热过程 第六章热力学基础 例2氮气液化,把氮气放在一个绝热的汽缸中, 开始时,氮气的压强为50个标准大气压、温度为300K; 经急速膨胀后,其压强降至1个标准大气压,从而使氮 气液化·试问此时氮的温度为多少? 解氮气可视为理想气体,其液化过程为绝热过程。 p1=50×1.013×105Pa T=300K p1=1.013×105Pa 氮气为双原子气体由表查得y=1.40 T2=T(P2)-1/y=98.0K
6 – 5 理想气体的等温过程和绝热过程 第六章热力学基础 例2 氮气液化, 把氮气放在一个绝热的汽缸中. 开始时,氮气的压强为50个标准大气压、温度为300K; 经急速膨胀后,其压强降至 1个标准大气压,从而使氮 气液化 . 试问此时氮的温度为多少 ? 解 氮气可视为理想气体, 其液化过程为绝热过程. 氮气为双原子气体由表查得 =1.40 ( ) 98.0K ( 1)/ 1 2 2 = 1 = − p p T T 50 1.013 10 Pa 5 p1 = T1 = 300K 1.013 10 Pa 5 p1 =