
3-1质点和质点系的动量定理 第三章动量守恒定律和能量守恒定律 力的累积效应 F(t)对t积累→p,I F对产积累→W,E 冲量质点的动量定理 动量 mu F= dp d(mō) Fdt dp =d (mo) dt dt Fd1=万2-五=mi,-m 冲量 力对时间的积分(矢量)T=Fdt
3–1 质点和质点系的动量定理 第三章动量守恒定律和能量守恒定律 2 1 2 1 2 1 d v v F t p p m m t t = − = − 一 冲量 质点的动量定理 动量 v p = m t m t p F d d( d d v) = = d d d ( v) F t = p = m 力的累积效应 F r W E F t t p I , ( ) , → → 对 积累 对 积累 冲量 力对时间的积分(矢量) = 2 1 d t t I F t

3-1质点和质点系的动量定理: 第三章动量守恒定律和能量守恒定律 Fdt p2-p =mv2-mo 动量定理在给定的时间内,外力作用在质点 上的冲量,等于质点在此时间内动量的增量. ◆分量形式 (I=Fdt =moax-mus 7=1,i+1,j+1,k1=F,d=m2,-m 1.=F.dt mv2:-mv
3–1 质点和质点系的动量定理 第三章动量守恒定律和能量守恒定律 动量定理 在给定的时间内,外力作用在质点 上的冲量,等于质点在此时间内动量的增量 . 2 1 2 1 2 1 d v v F t p p m m t t = − = − I I i I j I k x y z = + + 分量形式 z z t t z z y y t t y y x x t t x x I F t m m I F t m m I F t m m 2 1 2 1 2 1 2 1 2 1 2 1 d d d v v v v v v = = − = = − = = −
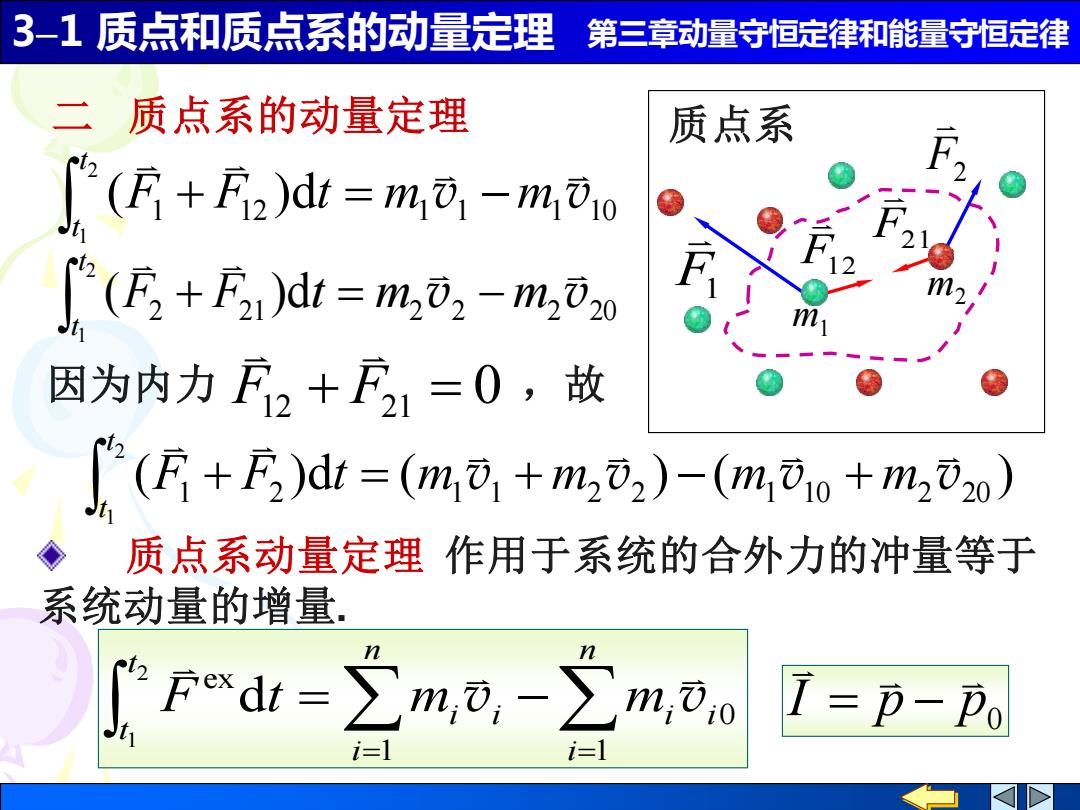
3-1质点和质点系的动量定理 第三章动量守恒定律和能量守恒定律 二质点系的动量定理 质点系 C(顶+f2k=m0,-m0o (E2+F1)dt=m,⑦2-m,⑦如 因为内力2+F1=0,故 (f+)dt=(m⑦,+m,元2)-(m,⑦o+m,元o) 质点系动量定理作用于系统的合外力的冲量等于 系统动量的增量. Fxdt=∑m,o,-∑ m,0 T=币-p0 i= i=l
3–1 质点和质点系的动量定理 第三章动量守恒定律和能量守恒定律 二 质点系的动量定理 质点系 m1 m2 F12 F21 F1 F2 质点系动量定理 作用于系统的合外力的冲量等于 系统动量的增量. = = = − n i i i i n i i t t F t m m 1 0 1 ex 2 1 d v v ( )d ( ) ( ) 1 2 1 1 2 2 1 10 2 20 2 1 v v v v F F t m m m m t t + = + − + 2 21 2 2 2 20 ( )d 2 1 v v F F t m m t t + = − 1 12 d 1 1 1 10 ( ) 2 1 v v F F t m m t t + = − 因为内力 F12 + F21 = 0 ,故 p p0 I = −
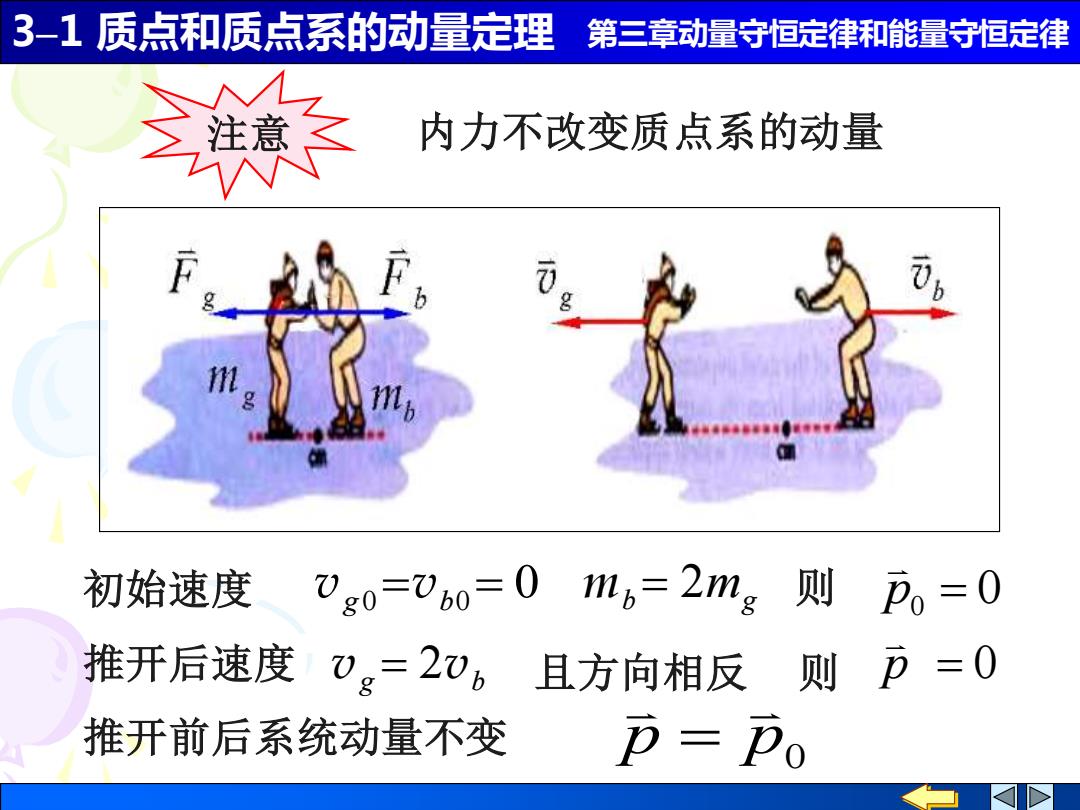
3-1质点和质点系的动量定理 第三章动量守恒定律和能量守恒定律 解 内力不改变质点系的动量 初始速度 0g0=0b0=01n,=2mg则p。=0 推开后速度0g=206且方向相反 则p=0 推开前后系统动量不变 p=卫o
3–1 质点和质点系的动量定理 第三章动量守恒定律和能量守恒定律 注意 内力不改变质点系的动量 b mg 0 m = 2 初始速度 vg 0 =vb0 = 则 p0 = 0 vg = 2vb p = 0 推开后速度 且方向相反 则 推开前后系统动量不变 p p0 =
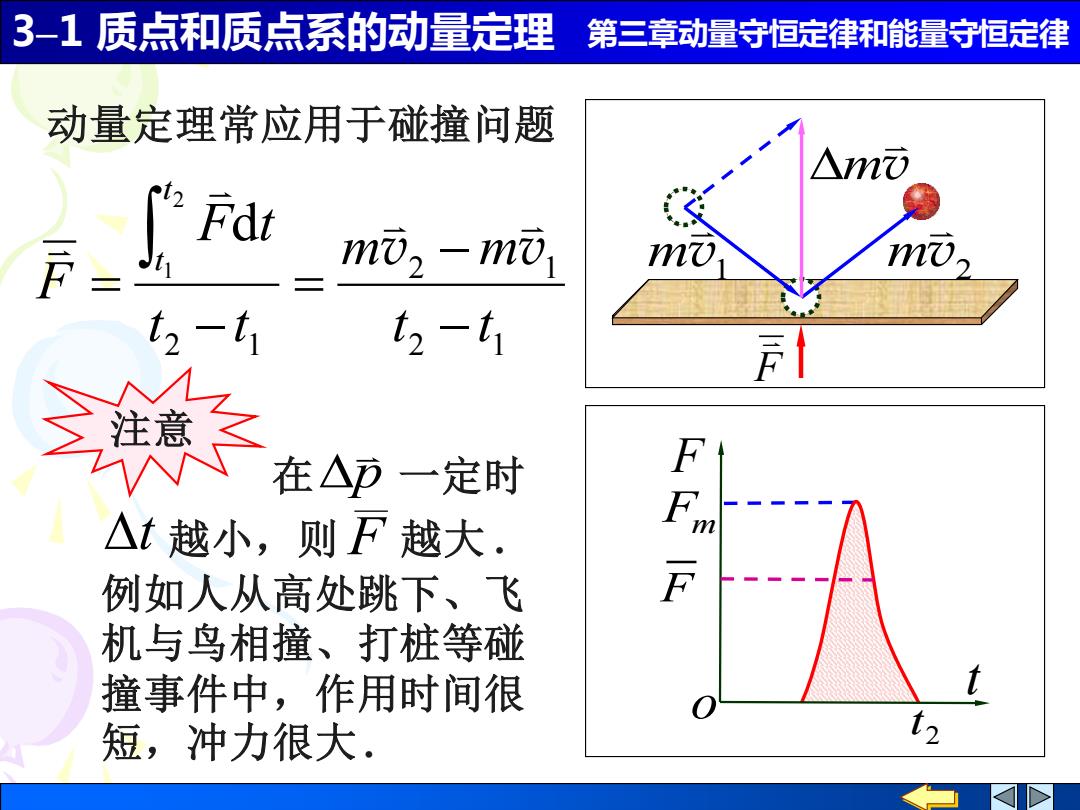
3-1质点和质点系的动量定理 第三章动量守恒定律和能量守恒定律 动量定理常应用于碰撞问题 mi,-mi mu. t2-t1 t2-t1 在△方一定时 F △t越小,则F越大. 例如人从高处跳下、飞 机与鸟相撞、打桩等碰 撞事件中,作用时间很 短,冲力很大 t
3–1 质点和质点系的动量定理 第三章动量守恒定律和能量守恒定律 v1 m v2 m v m 2 1 2 1 2 1 2 1 d t t m m t t F t F t t − − = − = v v 动量定理常应用于碰撞问题 F 1 t F Fm 2 t F t o 越小,则 越大 . 例如人从高处跳下、飞 机与鸟相撞、打桩等碰 撞事件中,作用时间很 短,冲力很大 . 注意 t F 在 p 一定时

3-1质点和质点系的动量定理 第三章动量守恒定律和能量守恒定律 例1一质量为0.05kg、速率为10ms的刚球,以与 钢板法线呈45°角的方向撞击在钢板上,并以相同的速率 和角度弹回来.设碰撞时间为0.05s.求在此时间内钢板所 受到的平均冲力F. 解建立如图坐标系,由动量定理得 F△t=m02x-m01x mvcosa-(-mvcosa) -2mucosa F,△t=2y-m0y musina -musin a =0 F-F- 2mv cosa 2=14.1N 方向沿X轴反向 △t
3–1 质点和质点系的动量定理 第三章动量守恒定律和能量守恒定律 例 1 一质量为0.05kg、速率为10m·s-1的刚球,以与 钢板法线呈45º角的方向撞击在钢板上,并以相同的速率 和角度弹回来 .设碰撞时间为0.05s.求在此时间内钢板所 受到的平均冲力 . v1 m v2 m x y 解 建立如图坐标系, 由动量定理得 = 2mvcos = mvsinα − mvsin = 0 F 14.1N 2 cos = = = t m F Fx v 方向沿 x 轴反向 x x x F t = mv2 − mv1 = mvcos −(−mvcos) y m y m y F t = v2 − v1
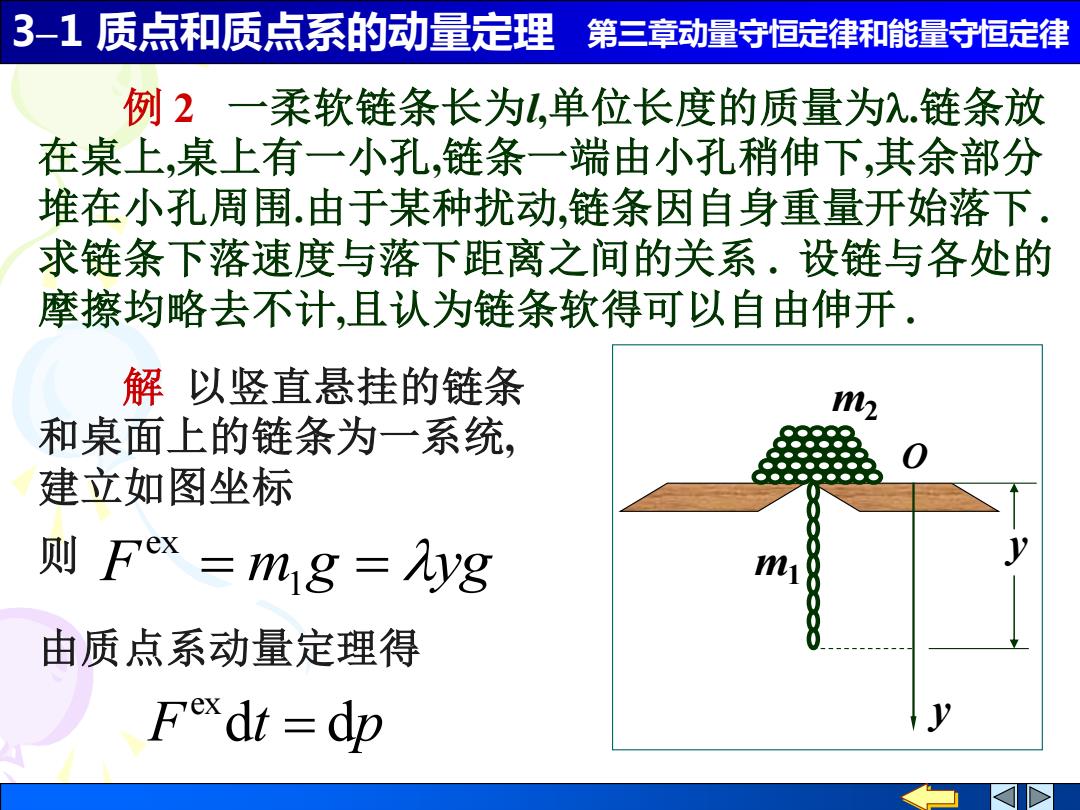
3-1质点和质点系的动量定理 第三章动量守恒定律和能量守恒定律 例2一柔软链条长为L,单位长度的质量为入.链条放 在桌上,桌上有一小孔,链条一端由小孔稍伸下,其余部分 堆在小孔周围.由于某种扰动,链条因自身重量开始落下. 求链条下落速度与落下距离之间的关系.设链与各处的 摩擦均略去不计,且认为链条软得可以自由伸开. 解以竖直悬挂的链条 和桌面上的链条为一系统, 建立如图坐标 则Fex=m1g=yg 由质点系动量定理得 Fexdt dp
3–1 质点和质点系的动量定理 第三章动量守恒定律和能量守恒定律 例 2 一柔软链条长为l,单位长度的质量为.链条放 在桌上,桌上有一小孔,链条一端由小孔稍伸下,其余部分 堆在小孔周围.由于某种扰动,链条因自身重量开始落下 . 求链条下落速度与落下距离之间的关系 . 设链与各处的 摩擦均略去不计,且认为链条软得可以自由伸开 . 解 以竖直悬挂的链条 和桌面上的链条为一系统, 建立如图坐标 由质点系动量定理得 F dt dp ex = m1 m2 O y y F = m1 g = yg 则 ex

3-1质点和质点系的动量定理 第三章动量守恒定律和能量守恒定律 Fexdt =dp 又 dp=九d(yw) .Aygdt =Ad(yo) 则 d(6w) 8= dt 两边同乘以ydy则 y湾bdd6 3 gy'dy-"wd(w)
3–1 质点和质点系的动量定理 第三章动量守恒定律和能量守恒定律 则 ( ) dt d yv yg = 两边同乘以 y d y 则 ( ) v ( v) v y y y y g y y y d d d d d 2 = = t ( ) = v v v y y g y y y y 0 0 2 d d 2 1 = gy 3 2 v ( ) 3 2 2 1 3 1 gy = yv m1 m2 O y y ygdt = d( yv) 又 dp = d( yv) F dt dp ex =