
3-7完全弹性碰撞完全非弹性碰撞 第三章动量守恒定律和能量守恒定律 碰撞 两物体互相接触时间极短而互作用力较大 的相互作用.:Fx<Fn∴∑D,=C 完全弹性碰撞 两物体碰撞之后,它们的动能之 和不变. Ek=Ek+Ek2=C 非弹性碰撞由于非保守力的作用,两物体碰撞 后,使机械能转换为热能、声能,化学能等其他形式 的能量 完全非弹性碰撞两物体碰撞后,以同一速度运动
3–7完全弹性碰撞 完全非弹性碰撞 第三章动量守恒定律和能量守恒定律 完全非弹性碰撞 两物体碰撞后,以同一速度运动 . F F p C i i = ex in 碰撞 两物体互相接触时间极短而互作用力较大 的相互作用 . Ek = Ek1 + Ek2 =C 完全弹性碰撞 两物体碰撞之后, 它们的动能之 和不变 . 非弹性碰撞 由于非保守力的作用 ,两物体碰撞 后,使机械能转换为热能、声能,化学能等其他形式 的能量
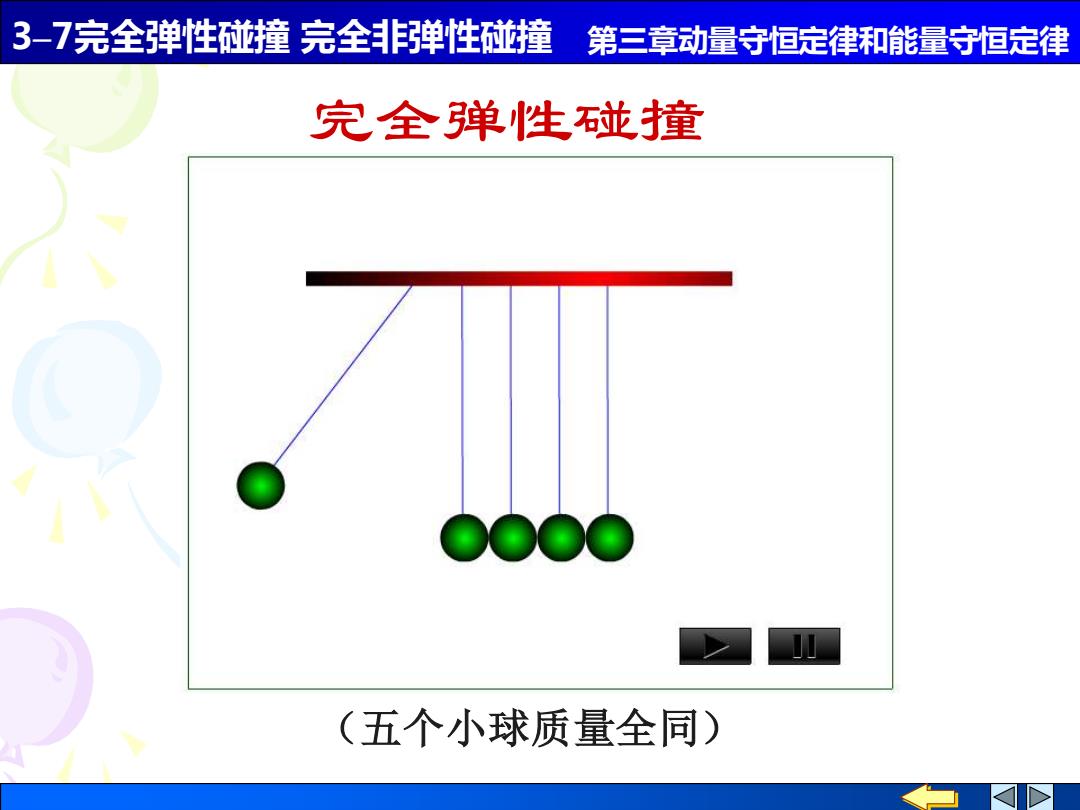
3-7完全弹性碰撞完全非弹性碰撞 第三章动量守恒定律和能量守恒定律 完全弹性碰撞 (五个小球质量全同)
3–7完全弹性碰撞 完全非弹性碰撞 第三章动量守恒定律和能量守恒定律 完全弹性碰撞 (五个小球质量全同)

3-7完全弹性碰撞完全非弹性碰撞 第三章动量守恒定律和能量守恒定律 例1在宇宙中有密度为p的尘埃,这些尘埃相对 惯性参考系是静止的.有一质量为mo的宇宙飞船以 初速)穿过宇宙尘埃,由于尘埃粘贴到飞船上,致使 飞船的速度发生改变.求飞船的速度与其在尘埃中飞 行时间的关系.(设想飞船的外形是面积为S的圆柱体) 解尘埃与飞船作完全 非弹性碰撞,把它们作为 一个系统,则动量守恒. 即 mvo my 得 dm moo dv=pSodt )2
3–7完全弹性碰撞 完全非弹性碰撞 第三章动量守恒定律和能量守恒定律 例 1 在宇宙中有密度为 的尘埃, 这些尘埃相对 惯性参考系是静止的 . 有一质量为 的宇宙飞船以 初速 穿过宇宙尘埃, 由于尘埃粘贴到飞船上, 致使 飞船的速度发生改变 . 求飞船的速度与其在尘埃中飞 行时间的关系 . (设想飞船的外形是面积为S的圆柱体) 0 v m0 m v 解 尘埃与飞船作完全 非弹性碰撞, 把它们作为 一个系 统, 则 动量守恒 . 即 m0 v0 = mv 得 v v v d d 2 m m0 0 = − = Svdt

3-7完全弹性碰撞完全非弹性碰撞 第三章动量守恒定律和能量守恒定律 已知 mo,7o,P. 求 )与t的关系. 解 dm movo do pSodi ro du J00 3 mo -)120 2 pSvot mo
3–7完全弹性碰撞 完全非弹性碰撞 第三章动量守恒定律和能量守恒定律 v t m v 已知 , , . m0 v0 求 与 的关系 . 解 v v v d d 2 m m0 0 = − = Svdt − = t t m S 0 0 0 3 d d 0 v v v v v 0 1 2 0 0 0 ) 2 ( v v v S t m m + =
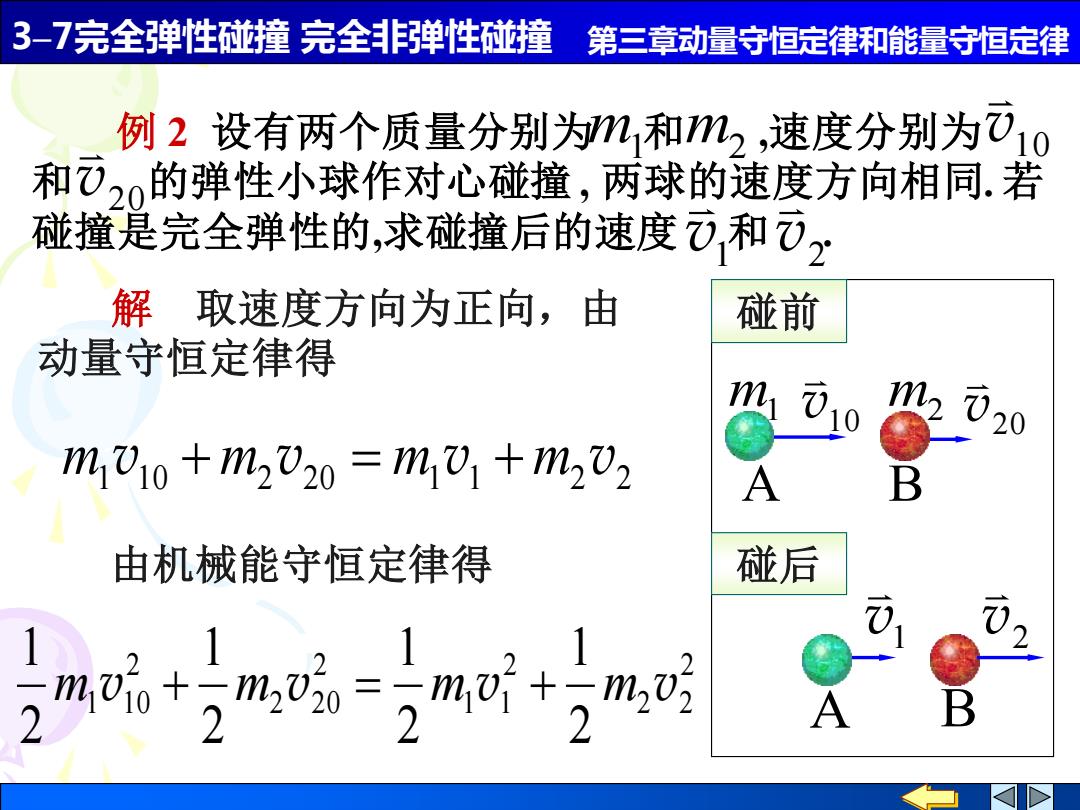
3-7完全弹性碰撞完全非弹性碰撞 第三章动量守恒定律和能量守恒定律 例2设有两个质量分别为m和m2,速度分别为010 和),的弹性小球作对心碰撞,两球的速度方向相同.若 碰撞是完全弹性的,求碰撞后的速度)和)2 解取速度方向为正向,由 碰前 动量守恒定律得 m 020 m1U10+m2V20=m,U1+m2V2 A B 由机械能守恒定律得 碰后 7 2,1 221 0i0十-m0。=-m,01+-m2, 2 2
3–7完全弹性碰撞 完全非弹性碰撞 第三章动量守恒定律和能量守恒定律 v20 例 2 设有两个质量分别为 和 ,速度分别为 和 的弹性小球作对心碰撞 , 两球的速度方向相同. 若 碰撞是完全弹性的,求碰撞后的速度 和 . m1 m2 v10 v1 v2 1 10 2 20 1 1 2 2 m v + m v = m v + m v 解 取速度方向为正向,由 动量守恒定律得 由机械能守恒定律得 2 2 2 2 1 1 2 2 2 0 2 1 1 0 2 1 2 1 2 1 2 1 m v + m v = m v + m v A m1 m2 v10 v20 B v1 v2 A B 碰前 碰后

3-7完全弹性碰撞完全非弹性碰撞 第三章动量守恒定律和能量守恒定律 m1'10+m2020=m,1+m2V2 碰前 >m1(0-01)=m2(2-V20) 名 00 1 1 21 。1 A 2 m听+2%2m时+2m,时 - 2 碰后 m(-)=m,(2-0n) 解 (m2-m1)V20+2m1010 01= (m-m)加o+2m,020,0, mm> m1+m2
3–7完全弹性碰撞 完全非弹性碰撞 第三章动量守恒定律和能量守恒定律 2 2 2 2 1 1 2 2 2 0 2 1 1 0 2 1 2 1 2 1 2 1 m v + m v = m v + m v ( ) ( ) 2 2 0 2 2 2 2 1 2 1 1 0 m v - v = m v − v ( ) ( ) 1 10 1 2 2 20 m v − v = m v − v 1 10 2 20 1 1 2 2 m v + m v = m v + m v 解得 , ( ) 2 1 2 1 2 1 0 2 2 0 1 m m m m m + − + = v v v 1 2 2 1 2 0 1 1 0 2 ( ) 2 m m m m m + − + = v v v A m1 m2 v10 v20 B v1 v2 A B 碰前 碰后
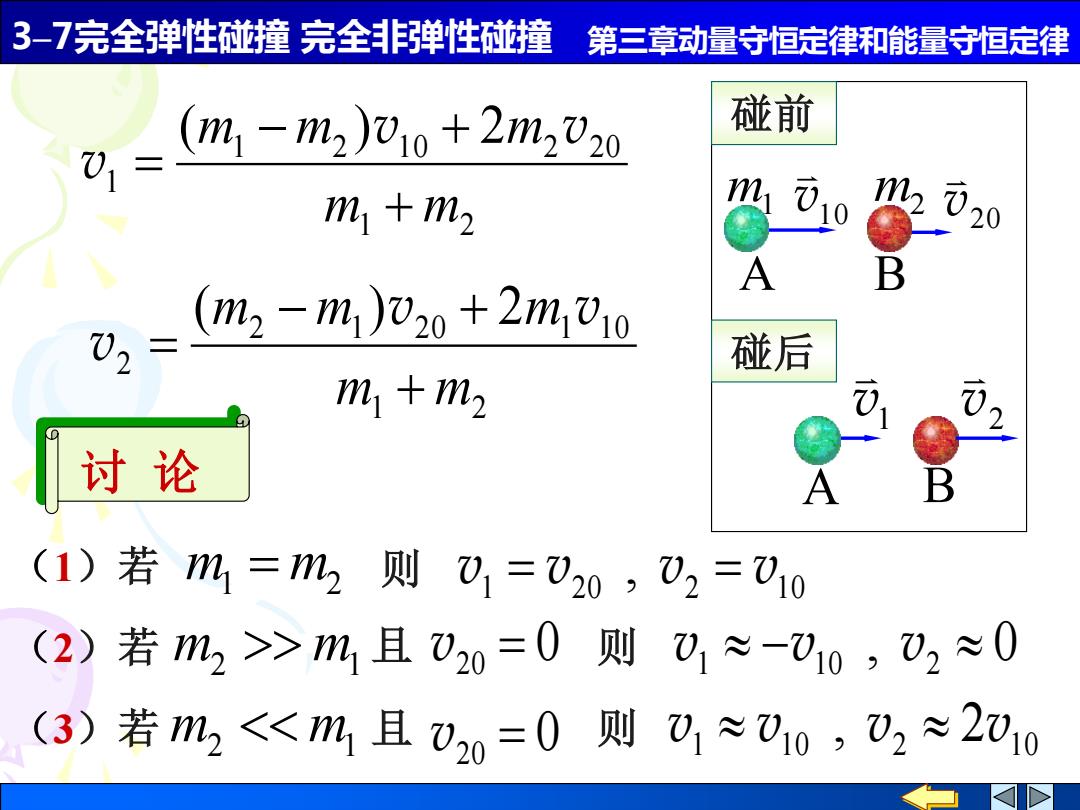
3-7完全弹性碰撞完全非弹性碰撞 第三章动量守恒定律和能量守恒定律 (m1-m2)010+2n2V20 碰前 m1+m2 m 1M2020 A B (2-m1)V20+2m,10 02= 碰后 mm> 讨论 (1)若m1=m2则)1=V20,02=010 (2)若m2>m1且020=0则0,1≈-010,02≈0 (3)若2<且V20=0则0≈010,2≈2010
3–7完全弹性碰撞 完全非弹性碰撞 第三章动量守恒定律和能量守恒定律 (1)若 m1 = m2 则 1 20 2 10 v = v , v = v (2)若 且 0 v20 = m2 m1 则 , 0 v1 −v10 v2 0 (3)若 m2 m1 且 v20 = 1 10 2 10 则 v v , v 2v 讨 论 1 2 1 2 1 0 2 2 0 1 ( ) 2 m m m m m + − + = v v v 1 2 2 1 2 0 1 1 0 2 ( ) 2 m m m m m + − + = v v v A m1 m2 10 v 20 v B v1 2 v A B 碰前 碰后

3-7完全弹性碰撞完全非弹性碰撞 第三章动量守恒定律和能量守恒定律 两个质子发生二维的完全弹性碰撞 两个质子在盛有 液态氢的容器中发生 弹性碰撞.一个质子 从左向右运动,与另 一个静止质子相碰撞, 碰撞后,两个质子的 运动方向相互垂直. 磁感强度的方向垂直 纸面向里
3–7完全弹性碰撞 完全非弹性碰撞 第三章动量守恒定律和能量守恒定律 两个质子在盛有 液态氢的容器中发生 弹性碰撞 . 一个质子 从左向右运动, 与另 一个静止质子相碰撞, 碰撞后, 两个质子的 运动方向相互垂直 . 磁感强度的方向垂直 纸面向里 . 两个质子发生二维的完全弹性碰撞