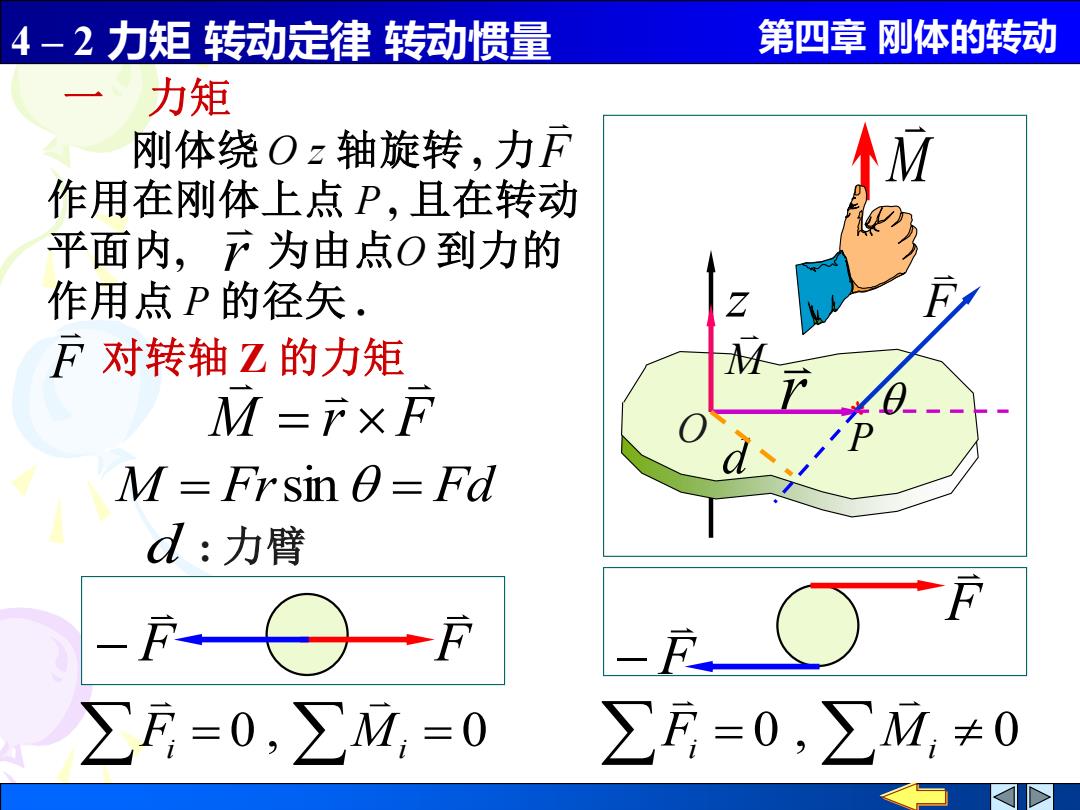
4-2力矩转动定律转动惯量 第四章刚体的转动 力矩 刚体绕Oz轴旋转,力F 作用在刚体上点P,且在转动 平面内,产为由点O到力的 作用点P的径矢. F对转轴Z的力矩 M=产xF M-Frsin 0=Fd d:力臂 ∑F=0,∑M,=0 ∑F=0,∑M,≠0
4 – 2 力矩 转动定律 转动惯量 第四章 刚体的转动 P z * O M = Frsin = Fd M F r d d : 力臂 刚体绕 O z 轴旋转 , 力 作用在刚体上点 P , 且在转动 平面内, 为由点O 到力的 作用点 P 的径矢 . F r M r F = F 对转轴 Z 的力矩 Fi = 0 , Mi = 0 Fi = 0 , Mi 0 F F − F F − 一 力矩 M
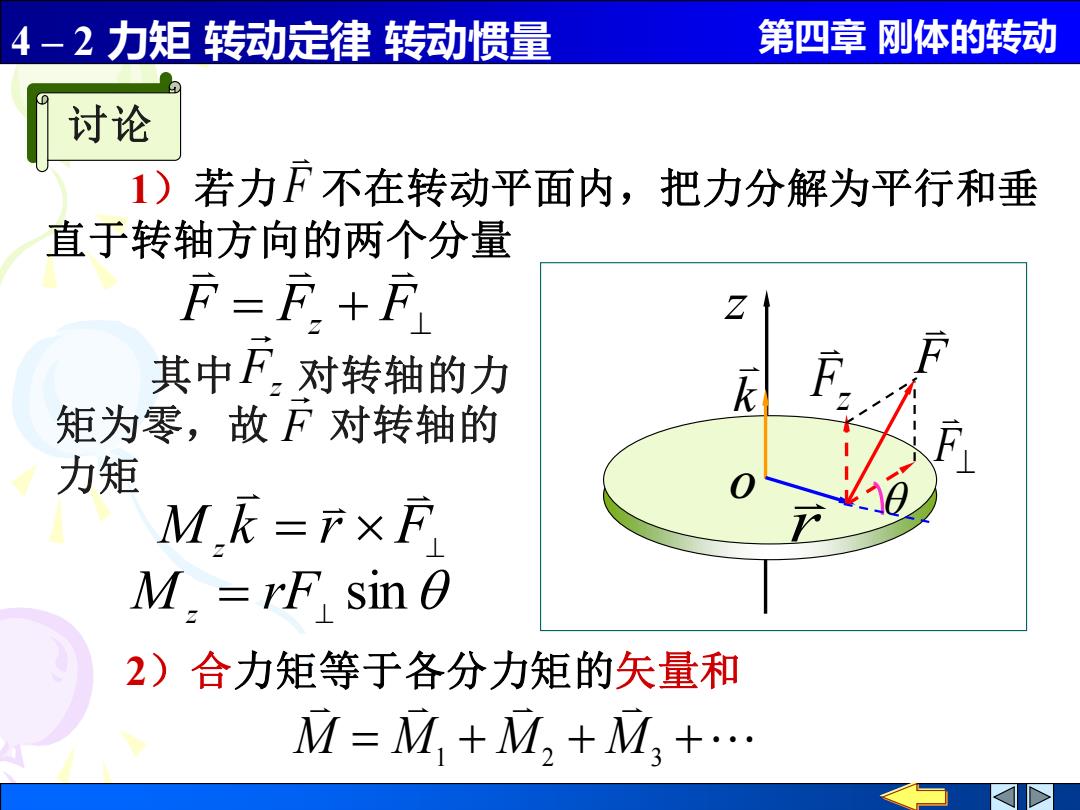
4-2力矩转动定律转动惯量 第四章刚体的转动 讨论 1)若力F不在转动平面内,把力分解为平行和垂 直于转轴方向的两个分量 F=F+F Z 其中F。对转轴的力 矩为零,故F对转轴的 力矩 ME=F×i M.=rF sin 0 2)合力矩等于各分力矩的矢量和 M=M,+M+M+
4 – 2 力矩 转动定律 转动惯量 第四章 刚体的转动 z O k F r 讨论 F = F z + F⊥ = F⊥ M k r z M z = rF⊥ sin Fz F⊥ 1)若力 不在转动平面内,把力分解为平行和垂 直于转轴方向的两个分量 F 2)合力矩等于各分力矩的矢量和 M = M1 + M2 + M3 + 其中 对转轴的力 矩为零,故 对转轴的 力矩 Fz F
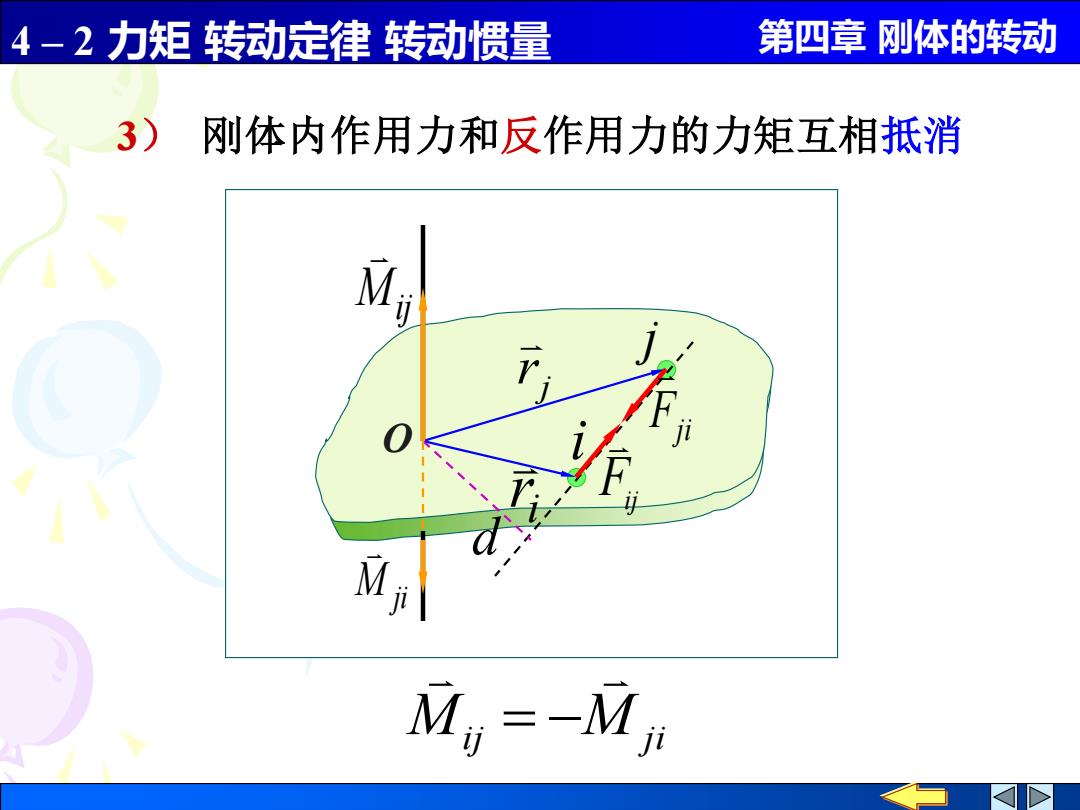
4-2力矩转动定律转动惯量 第四章刚体的转动 3)刚体内作用力和反作用力的力矩互相抵消 Mu=-Mm
4 – 2 力矩 转动定律 转动惯量 第四章 刚体的转动 3) 刚体内作用力和反作用力的力矩互相抵消 Mij M ji = − j r i r i j Fij Fji d O Mij M ji
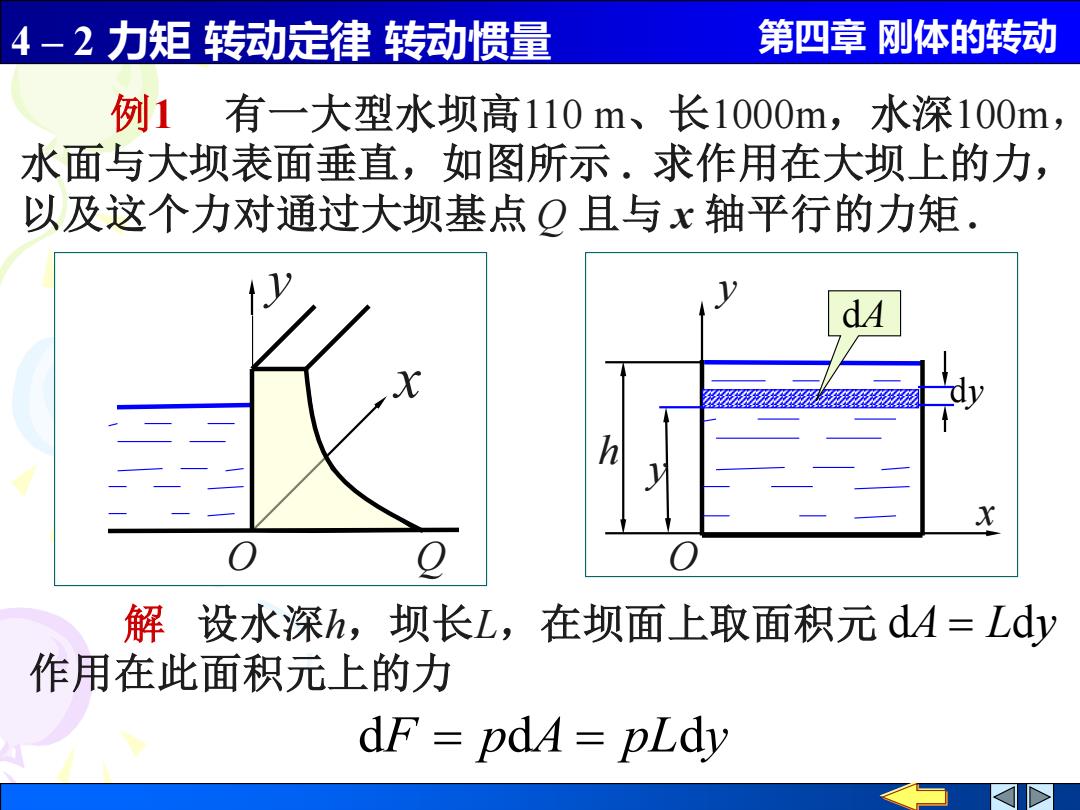
4-2力矩转动定律转动惯量 第四章刚体的转动 例1有一大型水坝高110m、长1000m,水深100m, 水面与大坝表面垂直,如图所示.求作用在大坝上的力, 以及这个力对通过大坝基点Q且与x轴平行的力矩. h 解设水深h,坝长L,在坝面上取面积元dA=Ldy 作用在此面积元上的力 dF pdA=pLdy
4 – 2 力矩 转动定律 转动惯量 第四章 刚体的转动 例1 有一大型水坝高110 m、长1000m,水深100m, 水面与大坝表面垂直,如图所示 . 求作用在大坝上的力, 以及这个力对通过大坝基点 Q 且与 x 轴平行的力矩 . 解 设水深h,坝长L,在坝面上取面积元 作用在此面积元上的力 dA = Ldy dF = pdA = pLdy y O h y x dA dy Q y O x

4-2力矩转动定律转动惯量 第四章刚体的转动 h=100m L=1000m dF pdA=pLdy 令大气压为P0,则 p=Po +pg(h-y) dF=[po+pg(h-y)]Ldy F-o+(h)dy=PoLh+ 代入数据,得 F=5.91×1010N
4 – 2 力矩 转动定律 转动惯量 第四章 刚体的转动 ( ) 0 p = p + g h − y 令大气压为 p0 ,则 dF [ p g(h y)]Ldy = 0 + − 2 0 0 0 2 1 F [ p g(h y)]Ldy p Lh gLh h = + − = + 代入数据,得 5.91 10 N 10 F = dF = pdA = pLdy y O h y x dA dy h =100m L =1000m

4一2力矩转动定律转动惯量 第四章刚体的转动 h=100mL=1000m dF =[po+pg(h-y)]Ldy dF对通过点Q的轴的力矩 dM ydF dM y[po+pg(h-y)]Ldy M=ypo+pg(h-y)ILdy 5a+N 代入数据,得 M=2.14×1012Nm
4 – 2 力矩 转动定律 转动惯量 第四章 刚体的转动 dM = ydF dM y[ p g(h y)]Ldy = 0 + − 2 3 0 6 1 2 1 = p Lh + gLh = + − h M y p g h y L y 0 [ 0 ( )] d 代入数据,得 2.14 10 N m 12 M = F 对通过点 Q 的轴的力矩 d y O Q h y dy F d dF [ p g(h y)]Ldy = 0 + − h =100m L =1000m
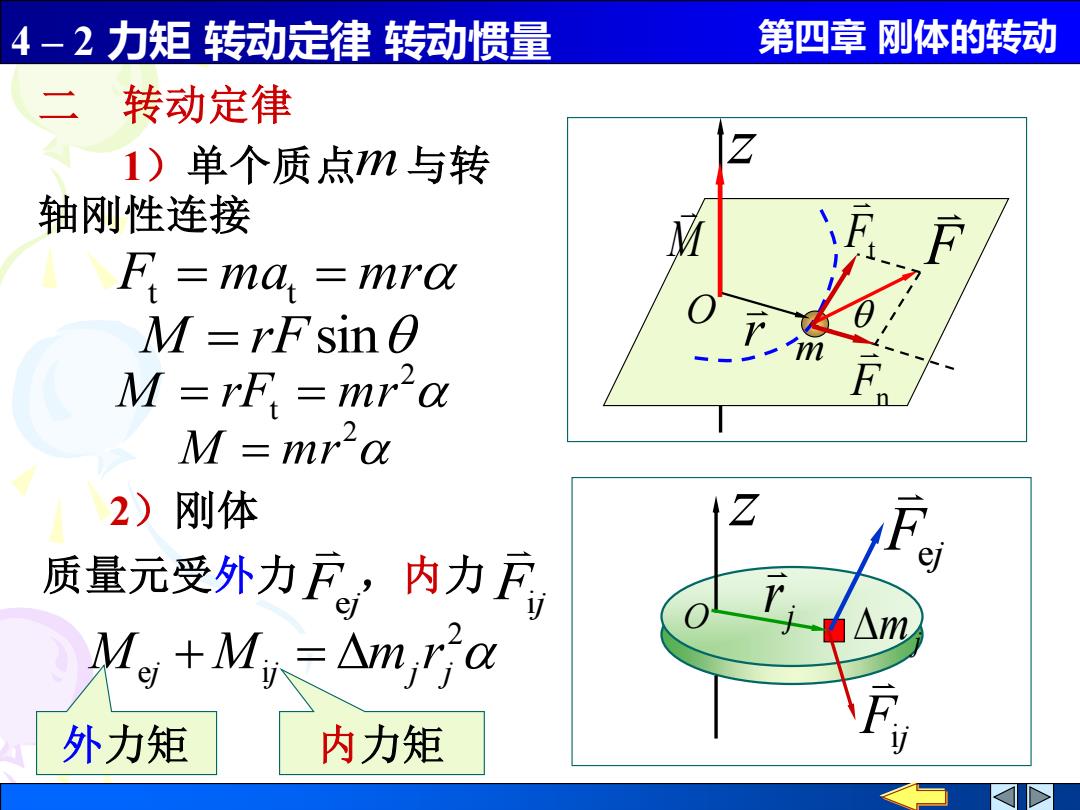
4-2力矩转动定律转动惯量 第四章刚体的转动 二转动定律 1)单个质点m与转 轴刚性连接 F=ma=mra M=rFsinO M=rF =mr'a M-mria 2)刚体 质量元受外力户,内力F Mg+M∈△n,a 外力矩 内力矩
4 – 2 力矩 转动定律 转动惯量 第四章 刚体的转动 O r m z 二 转动定律 F Ft Fn M = rFsin Ft = mat = mr 2 ej ij j j M + M = m r 2)刚体 质量元受外力 ,内力 Fej Fij M 1)单个质点 与转 轴刚性连接 m 外力矩 内力矩 2 M = mr 2 M = rFt = mr O z mj j r Fej Fij

4-2力矩转动定律转动惯量 第四章刚体的转动 ∑Mg+∑M,=∑Am,ra :Mg=-Mi÷∑M,=0 ∑Mg=(∑Am,月a 定义转动俊量J=∑A,片J=∫rdm 转动定律 M=Ja 刚体定轴转动的角加速度与它所受的合外力矩成 正比,与刚体的转动惯量成反比
4 – 2 力矩 转动定律 转动惯量 第四章 刚体的转动 刚体定轴转动的角加速度与它所受的合外力矩成 正比 ,与刚体的转动惯量成反比 . M M mj rj α j j j j 2 e + i = = − = 0 j Mi j M j i Mi j M mj rj )α j j 2 e = ( 转动定律 M = J 2 j j j 定义转动惯量 J = m r J r dm 2 = O z mj j r Fej Fij

4-2力矩转动定律转动惯量 第四章刚体的转动 三转动惯量 J=∑Am,r,J=jr2dm 物理意义:转动惯性的量度. 转动惯性的计算方法 质量离散分布刚体的转动惯量 J=∑Am,r=mr2+m,+… 质量连续分布刚体的转动惯量 J=∑Amr=jrdm dm:质量元
4 – 2 力矩 转动定律 转动惯量 第四章 刚体的转动 J m rj J r m j j , d 2 2 = = 三 转动惯量 ➢ 物理意义:转动惯性的量度 . ➢ 质量离散分布刚体的转动惯量 J = m rj 2 = m1 r1 2 + m2 r2 2 + j j 转动惯性的计算方法 ➢ 质量连续分布刚体的转动惯量 J m rj r m j j d 2 2 = = dm :质量元

4-2力矩转动定律转动惯量 第四章刚体的转动 >质量连续分布刚体的转动惯量 J=∑am,-=jrdm dm:质量元 日对质量线分布的刚体:dm=λdl 入:质量线密度 日对质量面分布的刚体:dm=OdS σ:质量面密度 F对质量体分布的刚体:dm=pdV 0:质量体密度
4 – 2 力矩 转动定律 转动惯量 第四章 刚体的转动 对质量线分布的刚体: :质量线密度 dm = dl 对质量面分布的刚体: :质量面密度 dm =dS 对质量体分布的刚体: :质量体密度 dm = dV dm :质量元 ➢ 质量连续分布刚体的转动惯量 J m rj r m j j d 2 2 = =