
7-4能量均分定律 理想气体内能 第七章气体动理论 自由度 3 -m) kT 2 2 =) 71 X 2欢 =-m) =kT 单原子分子平均能量 E=3×k7 2
7 – 4 能量均分定律 理想气体内能 第七章气体动理论 一 自由度 m kT 2 3 2 1 2 kt = v = 2 2 2 2 3 1 vx = vy = vz = v m x m y m z kT 2 1 2 1 2 1 2 1 2 2 2 v = v = v = 单原子分子平均能量 kT 2 1 = 3 y z x o
7-4能量均分定律理想气体内能 第七章气体动理论 刚性双原子分子 分子平均平动动能 2 =2m0+2m0 Cy 分子平均转动动能 Su-gJa+o
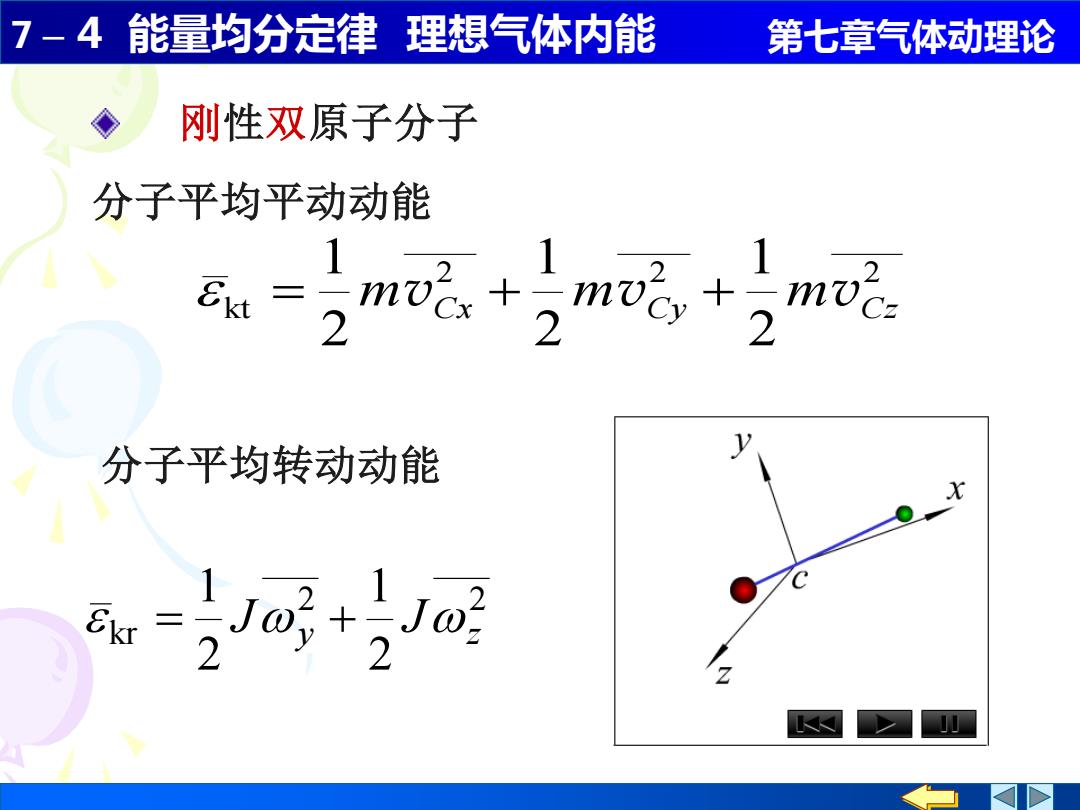
7 – 4 能量均分定律 理想气体内能 第七章气体动理论 刚性双原子分子 分子平均平动动能 2 2 2 kt 2 1 2 1 2 1 = mvC x + mvC y + mvC z 分子平均转动动能 2 2 kr 2 1 2 1 y z = J + J
7-4能量均分定律理想气体内能 第七章气体动理论 非刚性双原子分子 分子平均能量 y &=Ekt +Ekr m2 m 分子平均振动能量 OAAAAAO C 非刚性分子平均能量 &Ekt +8kr +Ey 自由度,分子能量中独立的速度和坐标的二次 方项数目叫做分子能量自由度的数目,简称自由度, 用符号i表示
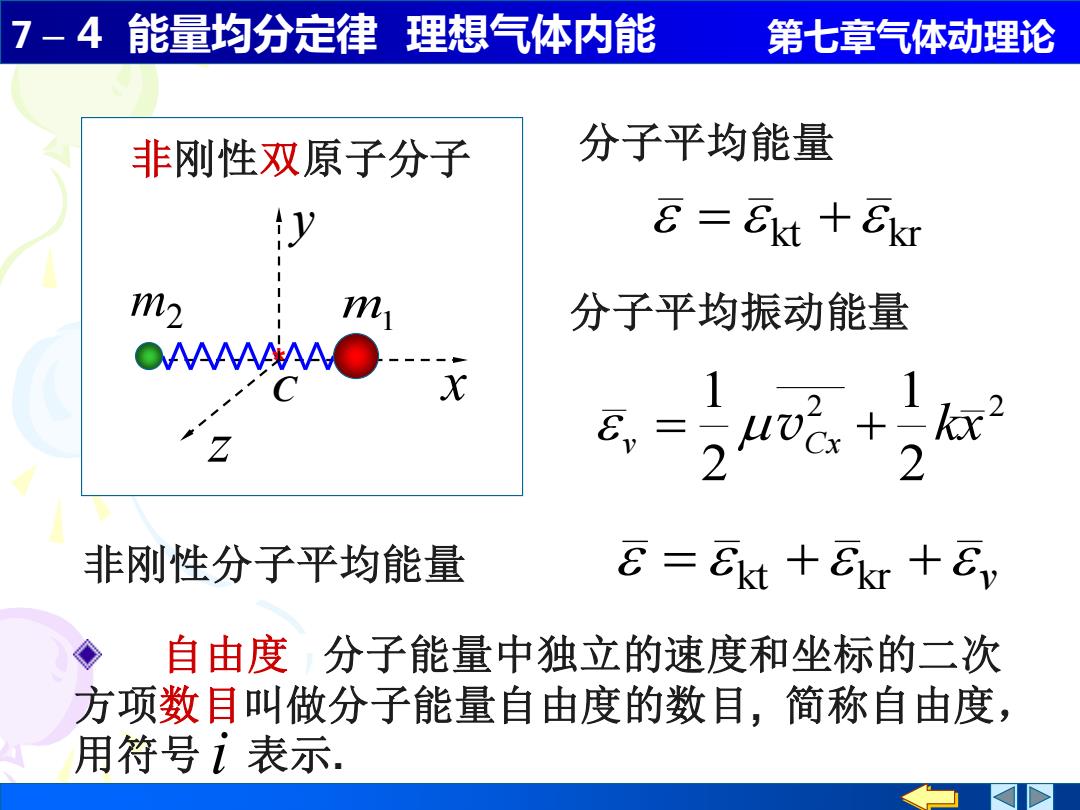
7 – 4 能量均分定律 理想气体内能 第七章气体动理论 2 2 2 1 2 1 kx v = vCx + 分子平均振动能量 kt kr = + 分子平均能量 v = + + 非刚性分子平均能量 kt kr 非刚性双原子分子 m2 m1 * C y z x 自由度 分子能量中独立的速度和坐标的二次 方项数目叫做分子能量自由度的数目, 简称自由度, 用符号 i 表示
7-4能量均分定律 理想气体内能 第七章气体动理论 自由度数目 i=t+r+v 哥 募 刚性分子能量自由度 自由度 分子 t平动 转动 i总 单原子分子 3 0 3 双原子分子 3 2 5 多原子分子 3 3 6
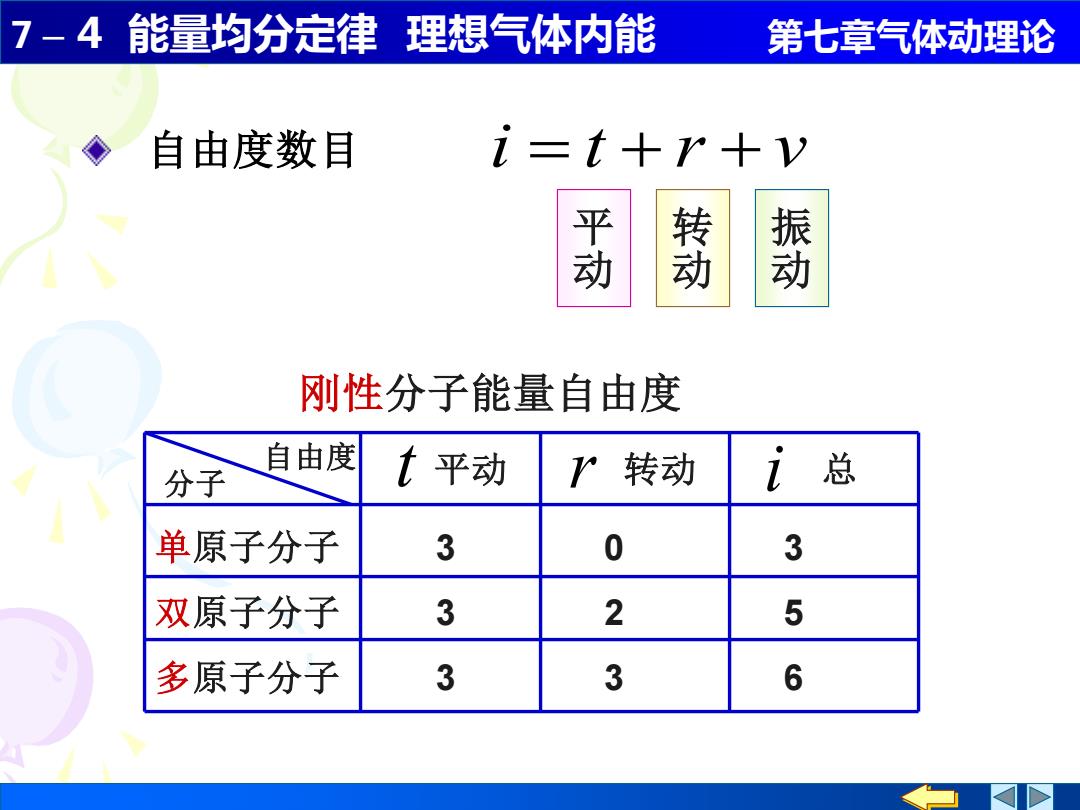
7 – 4 能量均分定律 理想气体内能 第七章气体动理论 自由度数目 i = t + r + v 平 动 转 动 振 动 单原子分子 3 0 3 双原子分子 3 2 5 多原子分子 3 3 6 刚性分子能量自由度 分子 t r i 自由度 平动 转动 总

7-4能量均分定律 理想气体内能 第七章气体动理论 能量均分定理(玻尔兹曼假设) 气体处于平衡态时,分子任何一个自由度的平 均能量都相等,均为】KT,这就是能量按自由度 2 均分定理. 分子的平均能量 E kT 2 三 理想气体的内能和摩尔热容 ◆ 理想气体的内能:分子动能和分子内原子间的 势能之和. 1mol理想气体的内能 E=NAE=RT 2
7 – 4 能量均分定律 理想气体内能 第七章气体动理论 三 理想气体的内能和摩尔热容 理想气体的内能 :分子动能和分子内原子间的 势能之和 . RT i E N 2 1 mol 理想气体的内能 = A = 二 能量均分定理(玻尔兹曼假设) 气体处于平衡态时,分子任何一个自由度的平 均能量都相等,均为 ,这就是能量按自由度 均分定理 . kT 2 1 分子的平均能量 k T i 2 =

7-4能量均分定律 理想气体内能 第七章气体动理论 m mol理想气体的内能E= RT M M2 dE m l i 理想气体内能变化 RdT M2 定体摩尔热容 Cvm 二 R 2 i+ 定压摩尔热容 Cp R 2 C四 i+2 摩尔热容比 Y
7 – 4 能量均分定律 理想气体内能 第七章气体动理论 mol 理想气体的内能 M m RT i M m E 2 = R T i M m E d 2 理想气体内能变化 d = R i CV 2 定体摩尔热容 ,m = R i Cp 2 2 ,m + 定压摩尔热容 = i i C C V p 2 ,m ,m + 摩尔热容比 = =