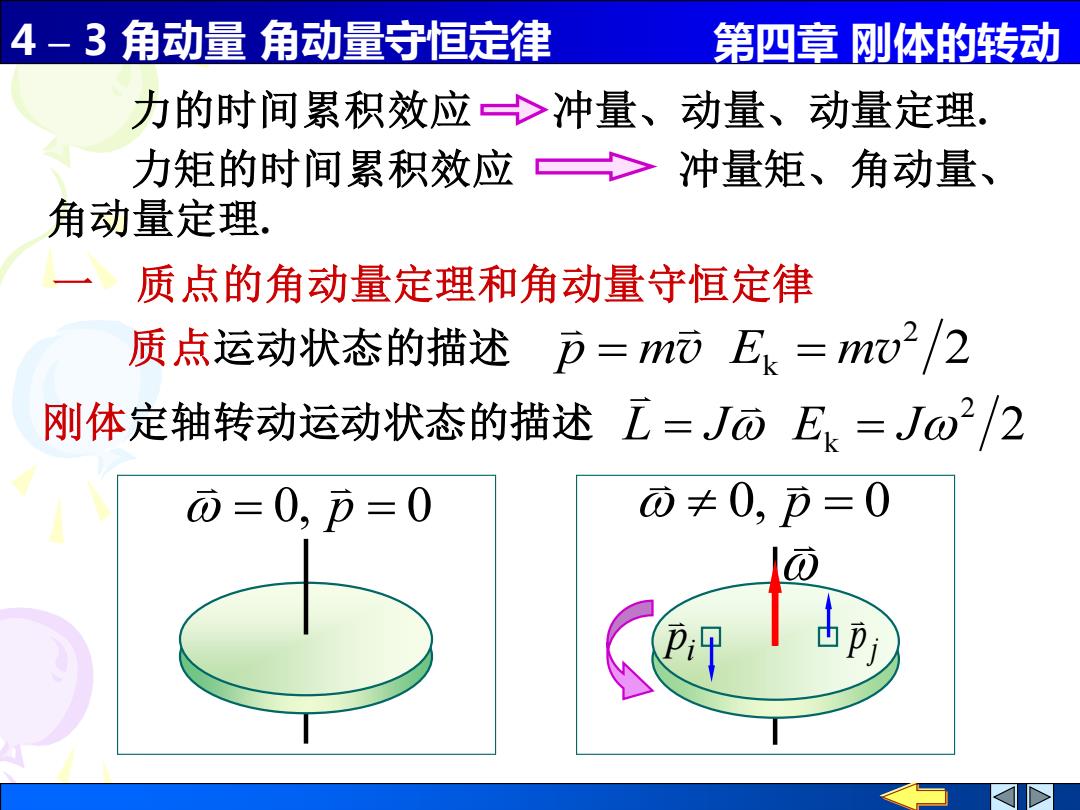
4-3角动量角动量守恒定律 第四章刚体的转动 力的时间累积效应>冲量、动量、动量定理. 力矩的时间累积效应>冲量矩、角动量、 角动量定理. 质点的角动量定理和角动量守恒定律 质点运动状态的描述 万=moE=m2/2 刚体定轴转动运动状态的描述工=JōE=Jω2/2 而=0,币=0 ⑦≠0,万=0
4 – 3 角动量 角动量守恒定律 第四章 刚体的转动 力矩的时间累积效应 冲量矩、角动量、 角动量定理. i p j p 0, p = 0 一 质点的角动量定理和角动量守恒定律 2 2 p = mv Ek = mv 质点运动状态的描述 力的时间累积效应 冲量、动量、动量定理. 2 2 L = J Ek = J 刚体定轴转动运动状态的描述 = 0, p = 0
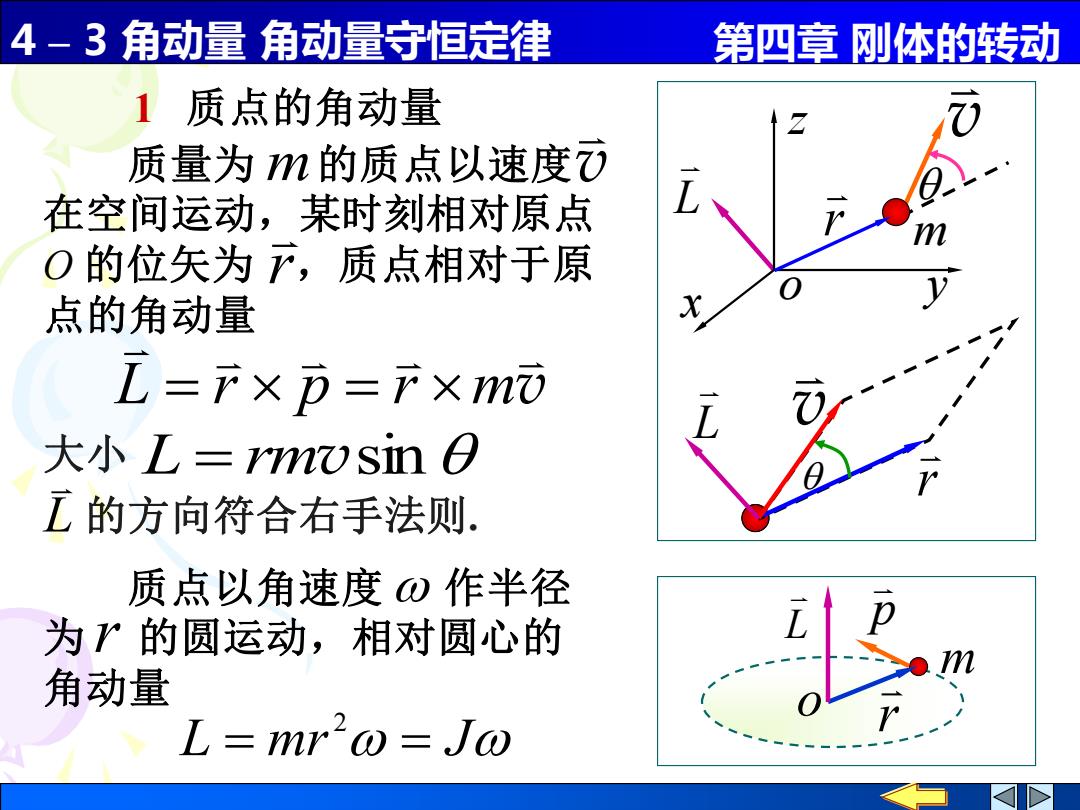
4-3角动量角动量守恒定律 第四章刚体的转动 1质点的角动量 质量为m的质点以速度) 在空间运动,某时刻相对原点 O的位矢为下,质点相对于原 点的角动量 L=产×p=下×mō 大小L=m)Sin0 工的方向符合右手法则, 质点以角速度®作半径 为严的圆运动,相对圆心的 角动量 L=mr'o=Jo
4 – 3 角动量 角动量守恒定律 第四章 刚体的转动 v 1 质点的角动量 v L = r p = r m v r L L r p m o 质点以角速度 作半径 为 的圆运动,相对圆心的 角动量 r L = mr = J 2 L r x y z o m 质量为 的质点以速度 在空间运动,某时刻相对原点 O 的位矢为 ,质点相对于原 点的角动量 m r v 大小 L = rmvsin L 的方向符合右手法则.

4-3角动量角动量守恒定律 第四章刚体的转动 2质点的角动量定理 i=r×p dp =F, dt dl d d面 d (×D)=F× dt dt dr dt dr dL =,⑦×p=0 dt dt dt 作用于质点的合力对参考点O M dl 的力矩,等于质点对该点O的角 动量随时间的变化率
4 – 3 角动量 角动量守恒定律 第四章 刚体的转动 ? d d , d d = = t L F t p p t r t p r p r t t L = = + d d d d ( ) d d d d t L M d d = 作用于质点的合力对参考点 O 的力矩 ,等于质点对该点 O 的角 动量随时间的变化率. r F t p r t L = = d d d d , 0 d d = p = t r v v 2 质点的角动量定理 L r p =

4-3角动量角动量守恒定律 第四章刚体的转动 M- dL Mdt=L2-L 冲量矩 '2 Mdt dt 质点的角动量定理:对同一参考点O,质点所受 的冲量矩等于质点角动量的增量 3质点的角动量守恒定律 M=0,= 恒矢量 质点所受对参考点O的合力矩为零时,质点对该 参考点O的角动量为一恒矢量
4 – 3 角动量 角动量守恒定律 第四章 刚体的转动 质点所受对参考点 O 的合力矩为零时,质点对该 参考点 O 的角动量为一恒矢量. M = L = 0, 恒矢量 冲量矩 M t t t d 2 1 质点的角动量定理:对同一参考点 O ,质点所受 的冲量矩等于质点角动量的增量. d 2 1 2 1 M t L L t t = − 3 质点的角动量守恒定律 t L M d d =

4-3角动量角动量守恒定律 第四章刚体的转动 例1一半径为R的光滑圆环置于竖直平面内.一质 量为m的小球穿在圆环上,并可在圆环上滑动.小球开始 时静止于圆环上的点A(该点在通过环心O的水平面上), 然后从A点开始下滑.设小球与圆环间的摩擦略去不计.求 小球滑到点B时对环心O的角动量和角速度. 解小球受重力和支持 力作用,支持力的力矩为零, 重力矩垂直纸面向里 M=mgRcos0 由质点的角动量定理 dl mgRcos0= dt
4 – 3 角动量 角动量守恒定律 第四章 刚体的转动 例1 一半径为 R 的光滑圆环置于竖直平面内.一质 量为 m 的小球穿在圆环上, 并可在圆环上滑动. 小球开始 时静止于圆环上的点 A (该点在通过环心 O 的水平面上), 然后从 A 点开始下滑.设小球与圆环间的摩擦略去不计.求 小球滑到点 B 时对环心 O 的角动量和角速度. 解 小球受重力和支持 力作用, 支持力的力矩为零, 重力矩垂直纸面向里 由质点的角动量定理 M = mgRcos t L mgR d d cos =

4-3角动量角动量守恒定律 第四章刚体的转动 mgR cos 0= dl dt dL mgR cos adt 考虑到 w-de/dt,L=mRv=mRa 得LdL=m2gR3cosd0 由题设条件积分上式 [LdL.=m'gR[cosa10 .·L=mR2o L =mRP(2g sin 0)2 -(2 sin 0) R
4 – 3 角动量 角动量守恒定律 第四章 刚体的转动 t L mgR d d cos = dL = mgRcosdt 考虑到 2 = d dt, L = mRv = mR d cosd 2 3 得 L L = m gR 由题设条件积分上式 = 0 2 3 0 LdL m gR cos d L 3 2 1 2 L = mR (2g sin ) 1 2 sin ) 2 ( R g = 2 L = mR
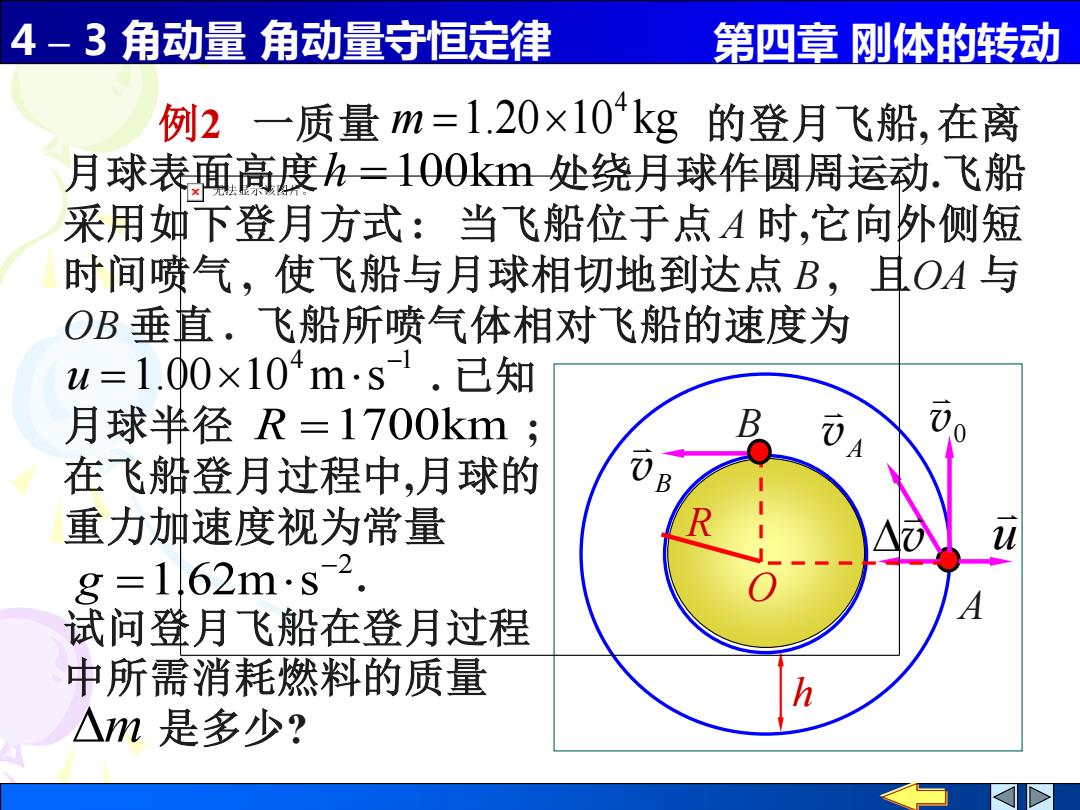
4-3角动量角动量守恒定律 第四章刚体的转动 例2一质量=1.20×104kg的登月飞船,在离 月球表面高度h=100km处绕月球作圆周运动.飞船 采用如下登月方式:当飞船位于点A时,它向外侧短 时间喷气,使飞船与月球相切地到达点B,且OA与 OB垂直.飞船所喷气体相对飞船的速度为 u=1.00×104ms.已知 月球半径R=1700km; 在飞船登月过程中,月球的 B 重力加速度视为常量 g=1,62ms2. 试问登月飞船在登月过程 中所需消耗燃料的质量 △m是多少?
4 – 3 角动量 角动量守恒定律 第四章 刚体的转动 例2 一质量 的登月飞船, 在离 月球表面高度 处绕月球作圆周运动.飞船 采用如下登月方式 : 当飞船位于点 A 时,它向外侧短 时间喷气 , 使飞船与月球相切地到达点 B , 且OA 与 OB 垂直 . 飞船所喷气体相对飞船的速度为 . 已知 月球半径 ; 在飞船登月过程中,月球的 重力加速度视为常量 . 试问登月飞船在登月过程 中所需消耗燃料的质量 m 是多少? 0 v A v B B v u v h O R A 1.20 10 kg 4 m = h =100km 4 1 1.00 10 m s − u = R =1700km 2 1.62m s − g =

4-3角动量角动量守恒定律 第四章刚体的转动 已知 m=1.20×104kg h=100km u=1.00×104ms1 R=1700km g=1.62ms-2 求所需消耗燃料的质量△m. 解设飞船在点A的 速度元o,月球质量mM, 由万有引力和牛顿定律 G mym -m (R+h)2 R+h 8=G R2
4 – 3 角动量 角动量守恒定律 第四章 刚体的转动 解 设飞船在点 A 的 速度 , 月球质量 mM , 由万有引力和牛顿定律 0 v R h m R h m m G + = + 2 0 2 M ( ) v 2 M R m g = G 0 v A v B vB u v h O R A 1.20 10 kg 4 m = h =100km 4 1 1.00 10 m s − u = R =1700km 2 1.62m s − g = 已知 求 所需消耗燃料的质量 m
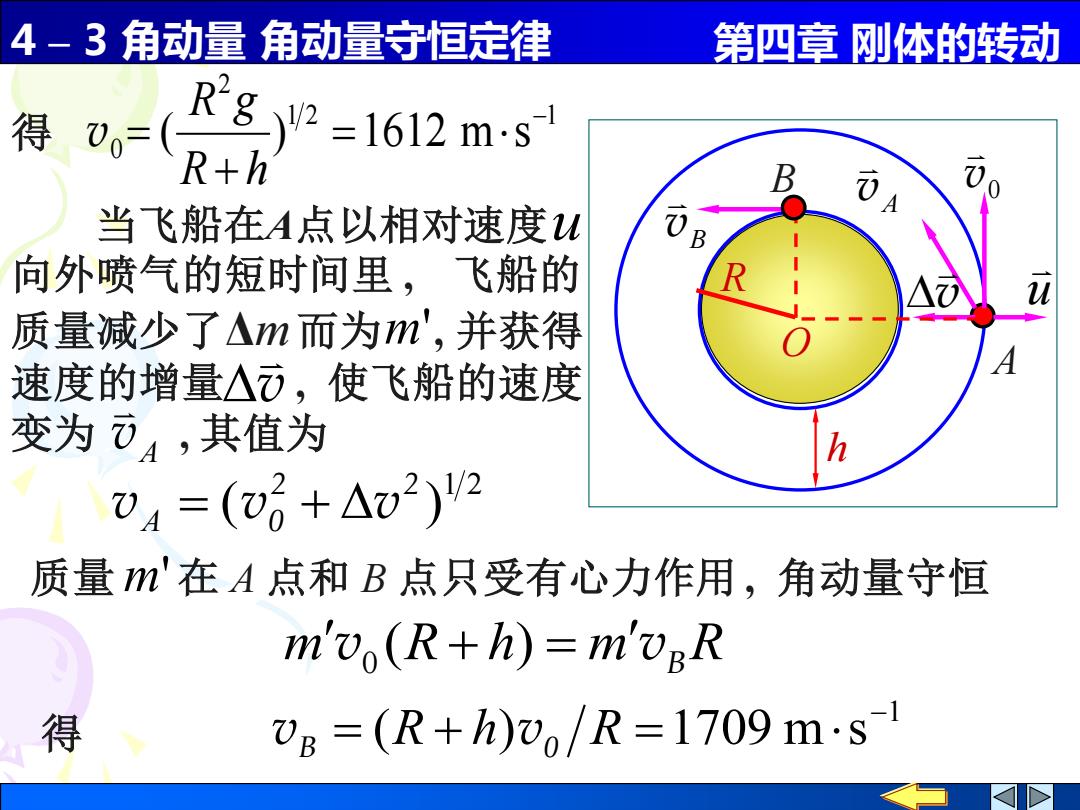
4-3角动量角动量守恒定律 第四章刚体的转动 得( R282=1612ms R+h 当飞船在A点以相对速度u 向外喷气的短时间里,飞船的 质量减少了△m而为m',并获得 速度的增量△⑦,使飞船的速度 变为⑦4,其值为 04=(+△o2)2 质量m'在A点和B点只受有心力作用,角动量守恒 m'vo(R+h)=m'UpR 得 'B=(R+h)vo/R=1709ms1
4 – 3 角动量 角动量守恒定律 第四章 刚体的转动 得 1 2 1 2 0 ( ) 1612 m s − = + = R h R g v 1 2 ( ) 2 2 vA = v0 + v m v0 (R + h) = m vB R 1 ( ) 1709 m s − = R + h R = 得 vB v0 当飞船在A点以相对速度 向外喷气的短时间里 , 飞船的 质量减少了Δm而为 , 并获得 速度的增量 , 使飞船的速度 变为 , 其值为 v A v m' u 质量 m' 在 A 点和 B 点只受有心力作用 , 角动量守恒 0 v vA B B v u v h O R A
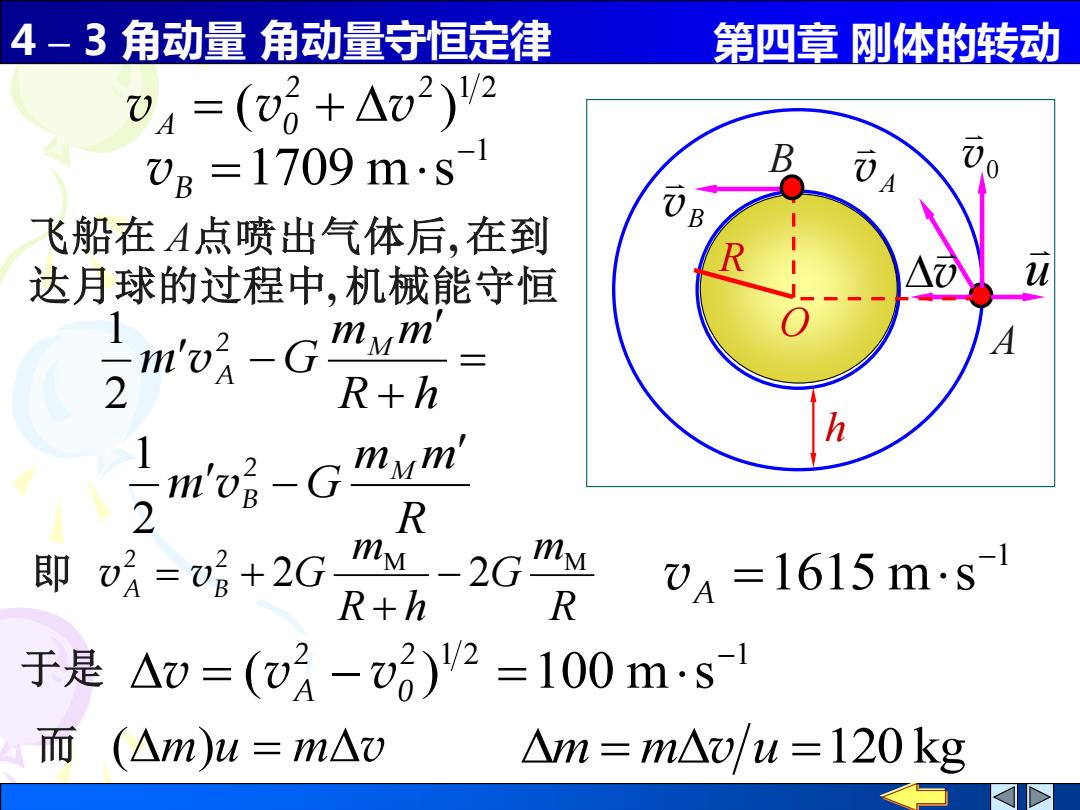
4-3角动量角动量守恒定律 第四章刚体的转动 04=(6+△2)2 VB=1709ms1 飞船在A点喷出气体后,在到 达月球的过程中,机械能守恒 1 mo-G mym 2 R+h 1 m'v8 -G mym' 2 R 即o听=话+2Gm1-2Gmu R 04=1615ms1 R+h 于是△=(o房-)2=100ms 而(△m)u=m△) △m=m△v/u=120kg
4 – 3 角动量 角动量守恒定律 第四章 刚体的转动 飞船在 A点喷出气体后, 在到 达月球的过程中, 机械能守恒 1 2 ( ) 2 2 vA = v0 + v 1 1709 m s − = vB R m m G R h m m G M M − = + − 2 B 2 A m v m v 2 1 2 1 R m G R h m G M M 2 − 2 + = + 2 B 2 即 vA v 1 1615 m s − = vA 于是 1 2 1 ( ) 100 m s − = − = 2 0 2 v vA v 而 (m)u = mv m = mv u =120 kg 0 v A v B B v u v h O R A