
2-3几种常见的力 第二章牛顿定律 万有引力 引力常量 F=G mm2 2 G=6.67x101N-m2.kg2 重力P=mg, 8= Gm≈9.80ms2 R 二弹性力 (压力,张力,弹簧弹性力等) 弹簧弹性力f=一x 三 摩擦力 滑动摩擦力F=FN 静摩擦力FD≤Fom From=4,F入 一般情况W≈4o
2 – 3 几种常见的力 第二章 牛顿定律 2 1 2 r m m F = G 一 万有引力 重力 P = mg, 2 9.80m s - 引力常量 11 2 2 6.67 10 N m kg − − G = 三 摩擦力 二 弹性力 一般情况 0 (压力,张力,弹簧弹性力等) 弹簧弹性力 f = −kx 滑动摩擦力 Ff = FN 静摩擦力 Ff0 Ff0m 2 R Gm g E = Ff0m = 0 FN
2-3几种常见的力 第二章牛顿定律 四种基本相互作用 力的种类 相互作用的物体 力的强度 力程 万有引力 一切质点 10-38 无限远 弱力 大多数粒子 10-13 小于10-1”m 电磁力 电荷 102 无限远 强力 核子、介子等 1¥ 10-5m 大以距源10-15m处强相互作用的力强度为1
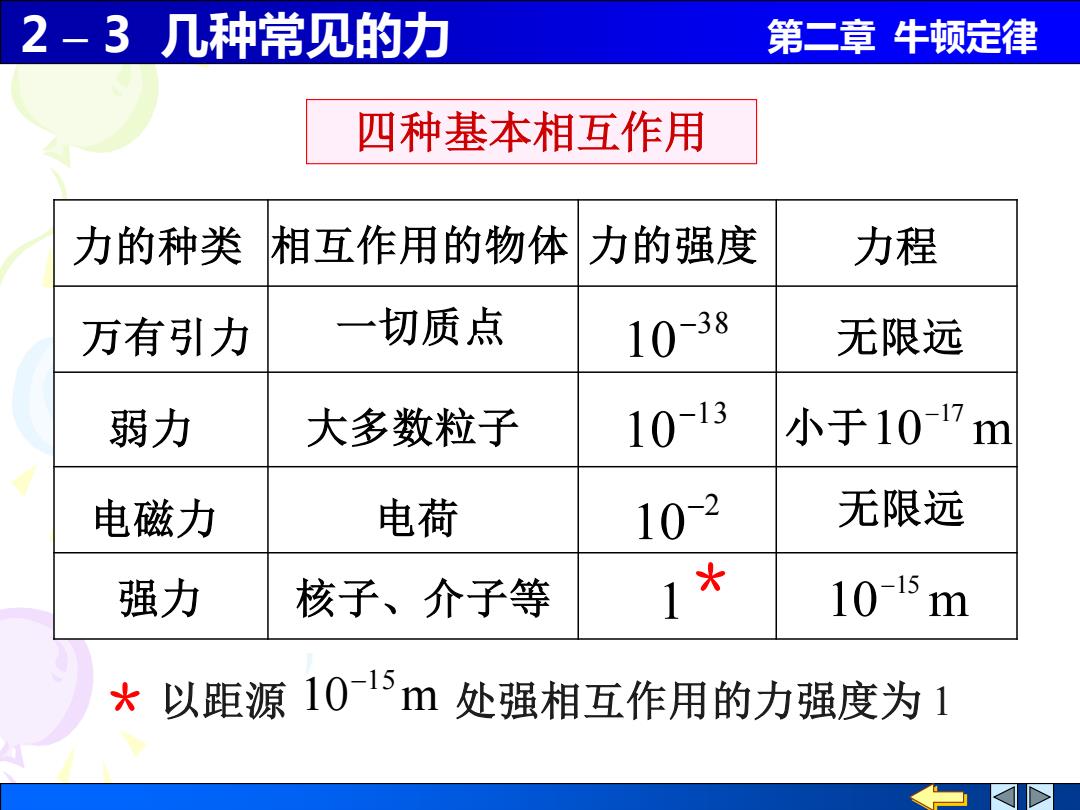
2 – 3 几种常见的力 第二章 牛顿定律 四种基本相互作用 * 以距源 10 m 处强相互作用的力强度为 1 −15 力的种类 相互作用的物体 力的强度 力程 万有引力 一切质点 10−38 无限远 弱力 大多数粒子 小于 10 m 13 −17 10− 电磁力 电荷 10−2 无限远 强力 核子、介子等 10 m −15 1 *

2-3几种常见的力 第二章牛顿定律 温伯格 弱相互作用 萨拉姆 电弱相互 格拉肖 电磁相互作用 作用理论 三人于1979年荣获诺贝尔物理学奖. 鲁比亚,范德米尔实验证明电弱相互作用, 1984年获诺贝尔奖. 电弱相互作用 强相互作用 “大统一”(尚待实现) 万有引力作用
2 – 3 几种常见的力 第二章 牛顿定律 温伯格 萨拉姆 格拉肖 弱相互作用 电磁相互作用 电弱相互 作用理论 三人于1979年荣获诺贝尔物理学奖 . 鲁比亚, 范德米尔实验证明电弱相互作用, 1984年获诺贝尔奖 . 电弱相互作用 强相互作用 万有引力作用 “大统一”(尚待实现)
2-3几种常见的力 第二章牛顿定律 例1质量为、长为l的柔软细绳,一端 系着放在光滑桌面上质量为m的物体,如图所示. 在绳的另一端加如图所示的力F.绳被拉紧时会略 现 有伸长(形变),一般伸长甚微,可略去不计. 设绳的长度不变,质量分布是均匀的.求:(1)绳 作用在物体上的力;(2)绳上任意点的张力. m IITITITIIITIITTIID m
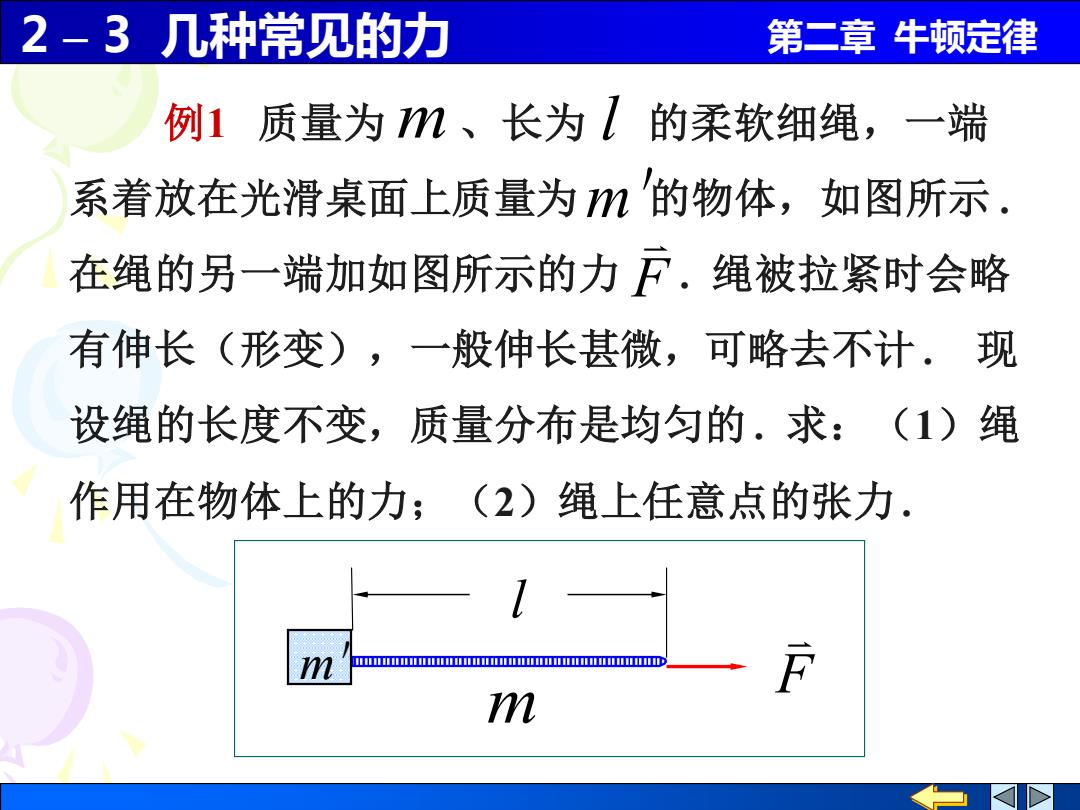
2 – 3 几种常见的力 第二章 牛顿定律 例1 质量为 、长为 的柔软细绳,一端 系着放在光滑桌面上质量为 的物体,如图所示 . 在绳的另一端加如图所示的力 . 绳被拉紧时会略 有伸长(形变),一般伸长甚微,可略去不计 . 现 设绳的长度不变,质量分布是均匀的 . 求:(1)绳 作用在物体上的力;(2)绳上任意点的张力 . m l m' F m' m l F
2-3几种常见的力 第二章牛顿定律 解设想在点P将绳分为两段 IIΦ F 其间张力F和F D 大小相等,方向相反 000iI0 (1) m mmmmmmmmmmmmmmmmmmmmm. a a FTo=FTo F a m'+m Fro-m'a m F-F'=ma F F m'+m
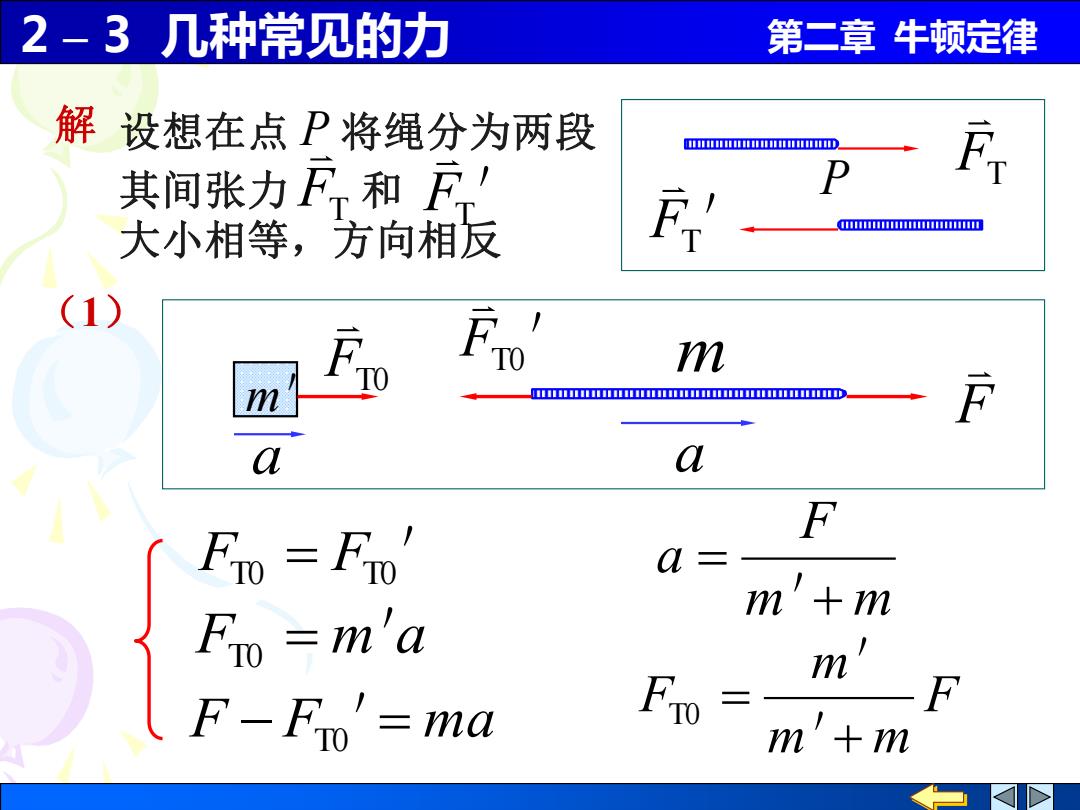
2 – 3 几种常见的力 第二章 牛顿定律 P FT FT ' 其间张力 和 大小相等,方向相反 FT FT ' (1) m' m F a a FT0 FT0 ' FT0 = FT0 ' FT0 = m'a F − FT0 ' = ma m m F a + = ' F m m m F + = ' ' T0 解 设想在点 P 将绳分为两段

2-3几种常见的力 第二章牛顿定律 (2)dm=mdx/I (F+dF)-F ommmmmmommmmm -(dm)a-"adx m mF dFT= dx (m'+m)l mF cmmmmm dx F=(m'+m5)- F I'm'+m
2 – 3 几种常见的力 第二章 牛顿定律 l (2) dx dm dx FT dm FT dFT + dm = mdx /l T T T (F +dF ) − Fx m m l mF F d ( ) d T + = ' + = lx FF x m m l mF F d ( ) d T T ' a x lm = ( d m ) a = d m m F lx F m m + = + ' ( ' ) T
2-3几种常见的力 第二章牛顿定律 例2如图绳索绕圆柱上, 绳绕圆柱张角为0,绳与圆 柱间的静摩擦因数为4,求 绳处于滑动边缘时,绳两端的 张力F4和FTB间关系.(绳 的质量忽略) y 解取一小段绕圆柱上的绳 取坐标如图 F.ods ds的张角dO ds两端的张力F,F+dF d0/2 do 圆柱对ds的摩擦力F 圆柱对ds的支持力F o
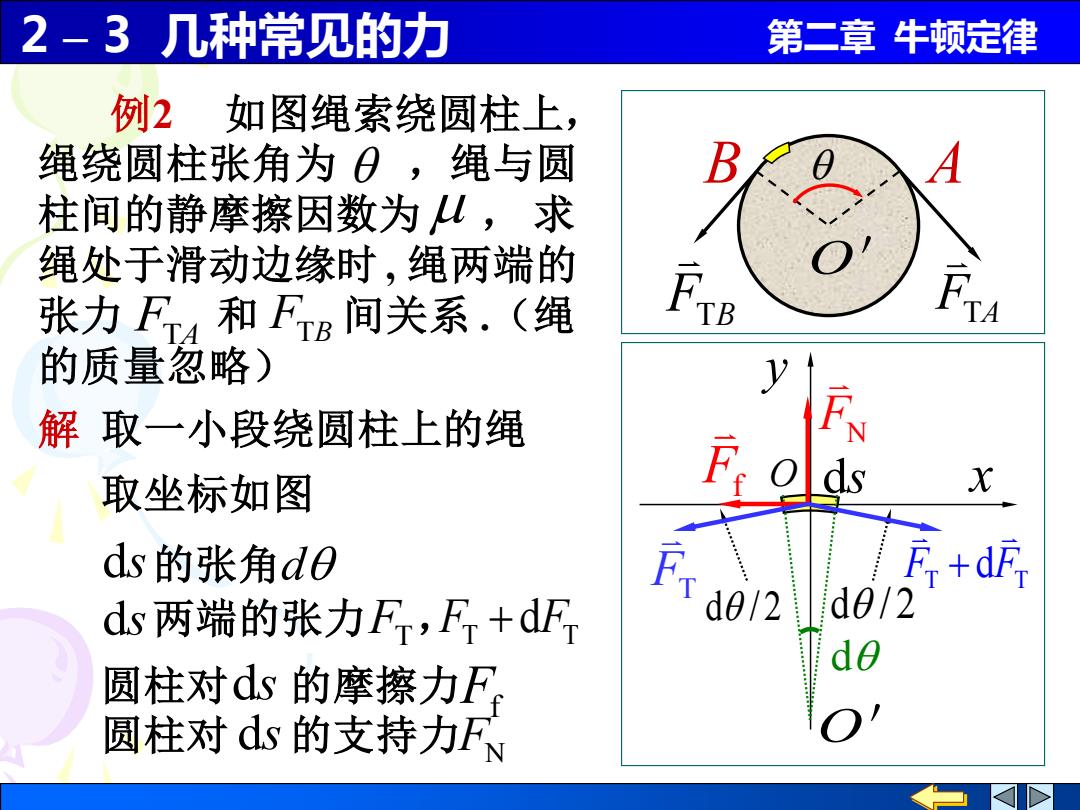
2 – 3 几种常见的力 第二章 牛顿定律 x y d O O' ds 例2 如图绳索绕圆柱上, 绳绕圆柱张角为 ,绳与圆 柱间的静摩擦因数为 , 求 绳处于滑动边缘时 , 绳两端的 张力 和 间关系 .(绳 的质量忽略) FTA FTB 圆柱对 的摩擦力 圆柱对 的支持力Ff FN ds ds 解 取一小段绕圆柱上的绳 取坐标如图 FT T T ds 两端的张力 , F + dF ds 的张角 d FTA FTB O' B A d / 2 d / 2 Ff FN FT T T F dF +

2-3几种常见的力 第二章牛顿定律 d dF )cos-F.cos 2 -F=0 2 A 9,m+-0 d -(+dF)sin do Fr=LFN dodo d F sin 2≈1 22 ∫df=F= Fra02a0i aEdo+Fdo-F do
2 – 3 几种常见的力 第二章 牛顿定律 0 2 d cos 2 d ( d ) cos T T T f F + F − F − F = 0 2 d sin 2 d ( )sin − FT + dFT − FT + FN = Ff = FN 1 2 d cos dFT = Ff = FN 2 d 2 d sin T T N d d d 2 1 F + F = F FTA FTB O' B A x y d O O' ds d / 2 d / 2 Ff FN FT T T F dF +
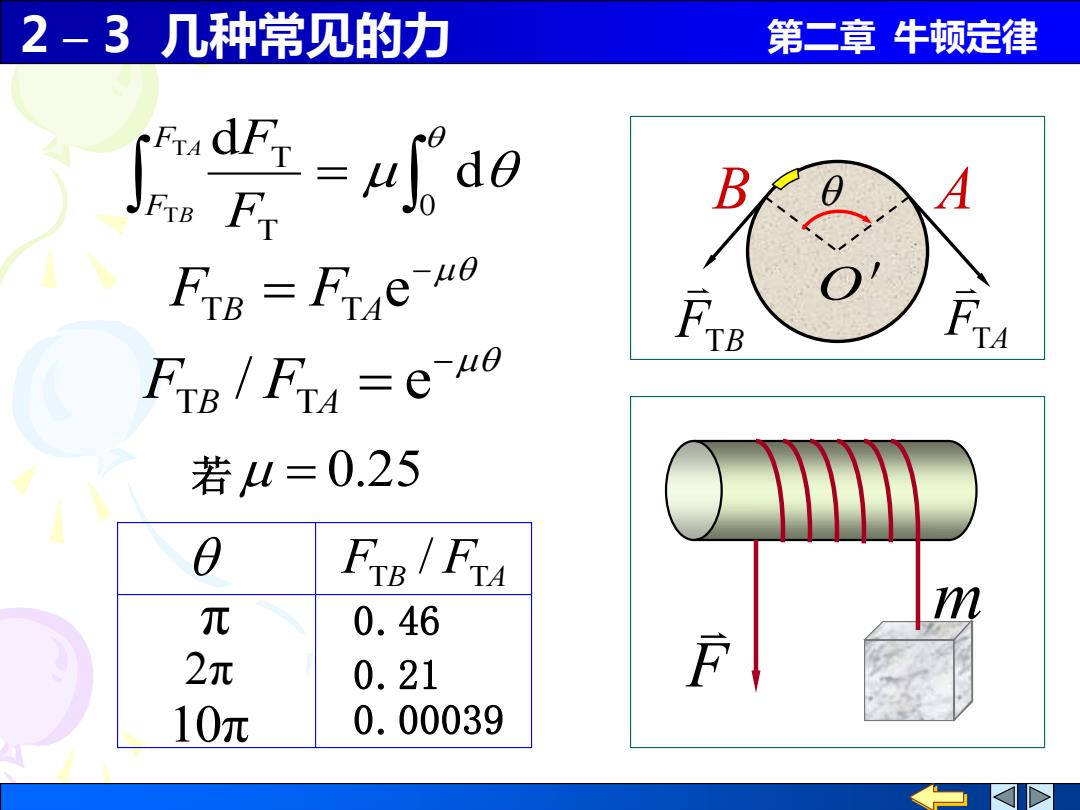
2-3几种常见的力 第二章牛顿定律 A FTB=Frae 4o FTB Fra =eo 若4=0.25 0 Fre/FA 兀 0.46 2π 0.21 10元 0.00039
2 – 3 几种常见的力 第二章 牛顿定律 − = e FTB FTA − / = e FTB FTA 若 = 0.25 FTB FTA / π 0.46 2π 0.21 10π 0.00039 = 0 T T d T d T A B F F F F FTA FTB O' B A m F