
16-5德布罗意波实物粒子的二象性 物理学教程 (第版) 法国物理学家德布罗意 (Louis Victor de Broglie 1892-1987) 思想方法自然界在许多方面都 是明显地对称的,他采用类比的方法 提出物质波的假设. “整个世纪以来,在辐射理论上,比起波动的研究 方法来,是过于忽略了粒子的研究方法;在实物理 论上,是否发生了相反的错误呢?是不是我们关于 ‘粒子’的图象想得太多,而过分地忽略了波的图 象呢?” 第十六章量子物理
物理学教程 (第二版) 第十六章 量子物理 16 – 5 德布罗意波 实物粒子的二象性 思想方法 自然界在许多方面都 是明显地对称的,他采用类比的方法 提出物质波的假设 . “整个世纪以来,在辐射理论上,比起波动的研究 方法来,是过于忽略了粒子的研究方法; 在实物理 论上,是否发生了相反的错误呢 ? 是不是我们关于 ‘粒子’的图象想得太多 ,而过分地忽略了波的图 象呢?” 法国物理学家德布罗意 (Louis Victor de Broglie 1892 – 1987 )

16-5德布罗意波实物粒子的二象性 物理学教程 (第二版 德布罗意假设(1924年) 德布罗意假设:实物粒子具有波粒二象性. E =hv p 德布罗意公式 h h E = mc2 V= p mv h h 注意 1)若 C则m=mo 2)宏观物体的德布罗意波长小到实验难以测量的 程度,因此宏观物体仅表现出粒子性. 第十六章量子物理
物理学教程 (第二版) 第十六章 量子物理 16 – 5 德布罗意波 实物粒子的二象性 一 德布罗意假设(1924 年 ) 德布罗意假设:实物粒子具有波粒二象性 . E = h h p = h mc h E 2 = = mv h p h 德布罗意公式 = = 2)宏观物体的德布罗意波长小到实验难以测量的 程度,因此宏观物体仅表现出粒子性 . 注 意 m m0 v →c = 1)若 则 若 则 v c m = m0

16-5德布罗意波实物粒子的二象性 物理学教程 (第二版) 例在一束电子中,电子的动能为200eV,求此 电子的德布罗意波长入? 解 v<<c,Ek=mo02 p=moy 26-84x10m91元=h=867×102m mo m U 此波长的数量级与X射线波长的数量级相当. 例计算质量m=0.01kg,速率v=300m/s 的子弹的德布罗意波长. λ= h6.63×1034 =2.21×10-34m 无法观察 mv 0.01×300 第十六章量子物理
物理学教程 (第二版) 第十六章 量子物理 16 – 5 德布罗意波 实物粒子的二象性 例 在一束电子中,电子的动能为 ,求此 电子的德布罗意波长 ? 200eV 解 v v 0 v 2 k 0 2 1 c, E = m p = m 6 1 0 k 8.4 10 m s 2 − = = m E v 8.67 10 nm2 0 − = = m v h 此波长的数量级与 X 射线波长的数量级相当. 2.21 10 m 0.01 300 6.63 10 3 4 3 4 − − = = = mv h 例 计算质量 , 速率 的子弹的德布罗意波长 . m = 0.01kg v = 300m s 无法观察
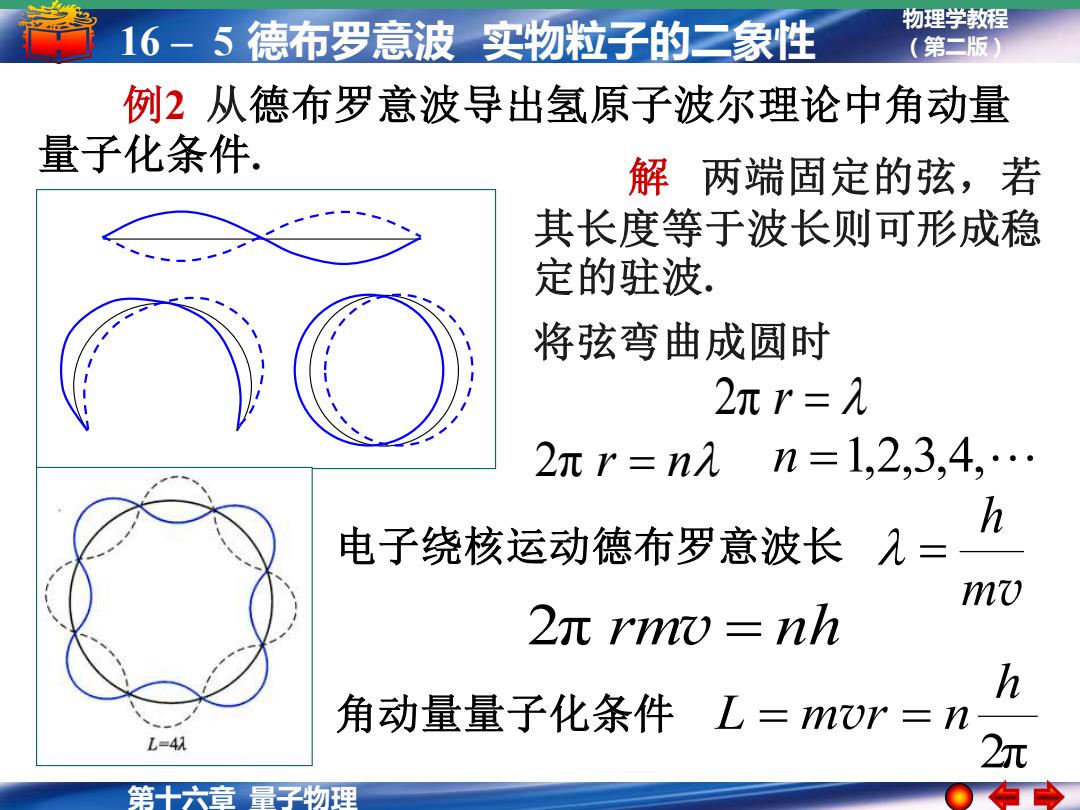
16-5德布罗意波实物粒子的二象性 物理学教程 (第二版) 例2从德布罗意波导出氢原子波尔理论中角动量 量子化条件. 解两端固定的弦,若 其长度等于波长则可形成稳 定的驻波. 将弦弯曲成圆时 2元r=λ 2πr=n元n=1,2,3,4,. h 电子绕核运动德布罗意波长九= mv 2元r)=nh h 角动量量子化条件L=m)r=n 2元 量子物理
物理学教程 (第二版) 第十六章 量子物理 16 – 5 德布罗意波 实物粒子的二象性 例2 从德布罗意波导出氢原子波尔理论中角动量 量子化条件. 2π r = n n =1,2,3,4, 2π rmv = nh 解 两端固定的弦,若 其长度等于波长则可形成稳 定的驻波. 2π r = 将弦弯曲成圆时 mv h 电子绕核运动德布罗意波长 = 2π h 角动量量子化条件 L = mvr = n
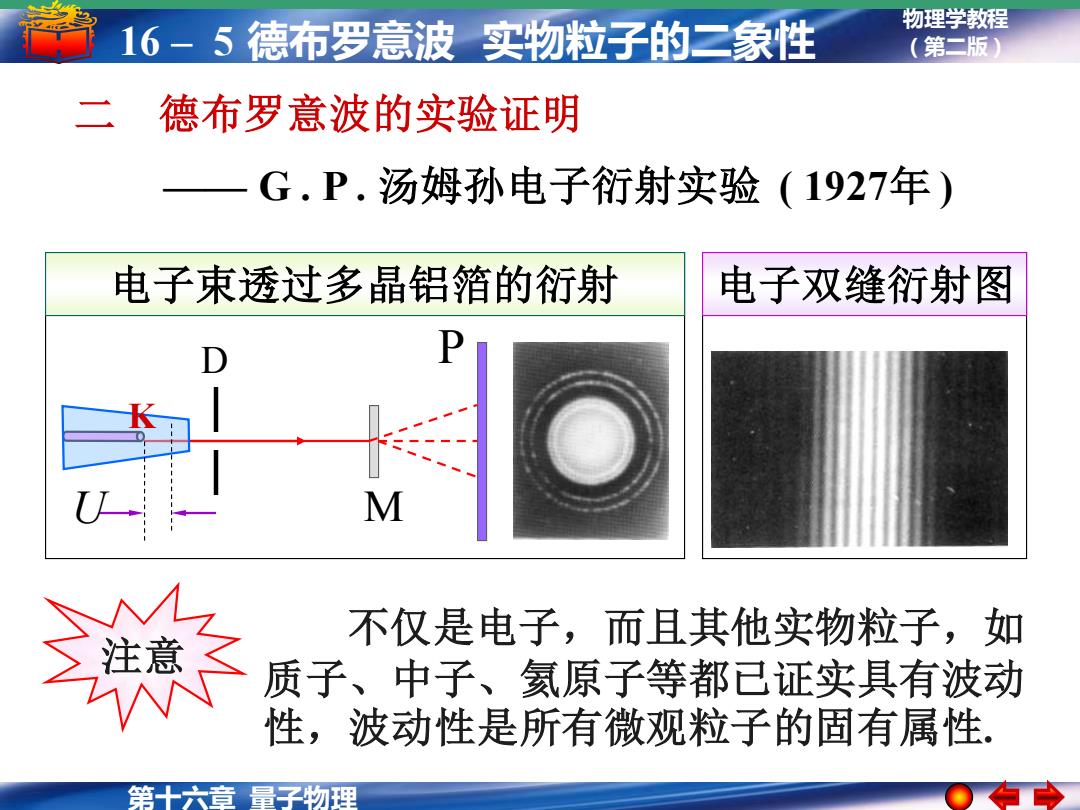
16-5德布罗意波实物粒子的二象性 物理学教程 (第二版) 二德布罗意波的实验证明 G.P.汤姆孙电子衍射实验(1927年) 电子束透过多晶铝箔的衍射 电子双缝衍射图 M L 不仅是电子,而且其他实物粒子,如 注意 质子、中子、氢原子等都已证实具有波动 性,波动性是所有微观粒子的固有属性 第十六章量子物理
物理学教程 (第二版) 第十六章 量子物理 16 – 5 德布罗意波 实物粒子的二象性 —— G . P . 汤姆孙电子衍射实验 ( 1927年 ) U M D P 电子束透过多晶铝箔的衍射 K 电子双缝衍射图 二 德布罗意波的实验证明 注意 不仅是电子,而且其他实物粒子,如 质子、中子、氦原子等都已证实具有波动 性,波动性是所有微观粒子的固有属性

物理学教程 16-5德布罗意波实物粒子的二象性 (第二版) 三 应用举例 1932年德国人鲁斯卡成功 研制了电子显微镜.(电子束 是有磁透镜聚焦后照射在样品 表面形成衍射图像) 目前分辨率:0.2nm 1981年德国人宾尼希和瑞 士人罗雷尔制成了扫瞄隧道显 电子显微镜下的 微镜.用于纳米材料、生命科 海棉针状体 学和微电子学的研究 横向分辨率:0.1nm, 纵向分辨率:0.001nm. 第十六章量子物理 有动
物理学教程 (第二版) 第十六章 量子物理 16 – 5 德布罗意波 实物粒子的二象性 三 应用举例 1932年德国人鲁斯卡成功 研制了电子显微镜 . (电子束 是有磁透镜聚焦后照射在样品 表面形成衍射图像) 目前分辨率:0.2nm 电子显微镜下的 海棉针状体 1981年德国人宾尼希和瑞 士人罗雷尔制成了扫瞄隧道显 微镜. 用于纳米材料、生命科 学和微电子学的研究. 横向分辨率:0.1nm, 纵向分辨率:0.001nm

物理学教程 16-5德布罗意波实物粒子的二象性 (第版) 四 德布罗意波的统计解释 经典粒子不被分割的整体,有确定位置和运动 轨道;经典的波某种实际的物理量的空间分布作周 期性的变化,波具有相干叠加性.二象性要求将 波和粒子两种对立的属性统一到同一物体上. 1926年玻恩提出德布罗意波是概率波. > 统计解释:在某处德布罗意波的强度是与粒子在 该处邻近出现的概率成正比的. >概率概念的哲学意义:在已知给定条件下,不可 能精确地预知结果,只能预言某些可能的结果的概率 第十六章量子物理
物理学教程 (第二版) 第十六章 量子物理 16 – 5 德布罗意波 实物粒子的二象性 四 德布罗意波的统计解释 经典粒子 不被分割的整体,有确定位置和运动 轨道 ;经典的波 某种实际的物理量的空间分布作周 期性的变化,波具有相干叠加性 . 二象性 要求将 波和粒子两种对立的属性统一到同一物体上 . 1926 年玻恩提出 德布罗意波是概率波 . ➢ 统计解释:在某处德布罗意波的强度是与粒子在 该处邻近出现的概率成正比的 . ➢ 概率概念的哲学意义:在已知给定条件下,不可 能精确地预知结果,只能预言某些可能的结果的概率