
1-1质点运动的描述 第一章质点运动学 参考系质点 1参考系 为描述物体的运动而选择的标准物叫做参考系, 选取的参考系不同,对物体运动情况的描述不 同,这就是运动描述的相对性. 2质点 如果我们研究某一物体的运动,而可以忽略其 大小和形状对物体运动的影响,若不涉及物体的转 动和形变,我们就可以把物体当作是一个具有质量 的点(即质点)来处理. 质点是经过科学抽象而形成的理想化的物理模 型.目的是为了突出研究对象的主要性质,暂不考 虑一些次要的因素
1 – 1 质点运动的描述 第一章质点运动学 一 参考系 质点 质点是经过科学抽象而形成的理想化的物理模 型 . 目的是为了突出研究对象的主要性质 , 暂不考 虑一些次要的因素 . 为描述物体的运动而选择的标准物叫做参考系. 1 参考系 如果我们研究某一物体的运动,而可以忽略其 大小和形状对物体运动的影响,若不涉及物体的转 动和形变,我们就可以把物体当作是一个具有质量 的点(即质点)来处理 . 2 质点 选取的参考系不同,对物体运动情况的描述不 同,这就是运动描述的相对性
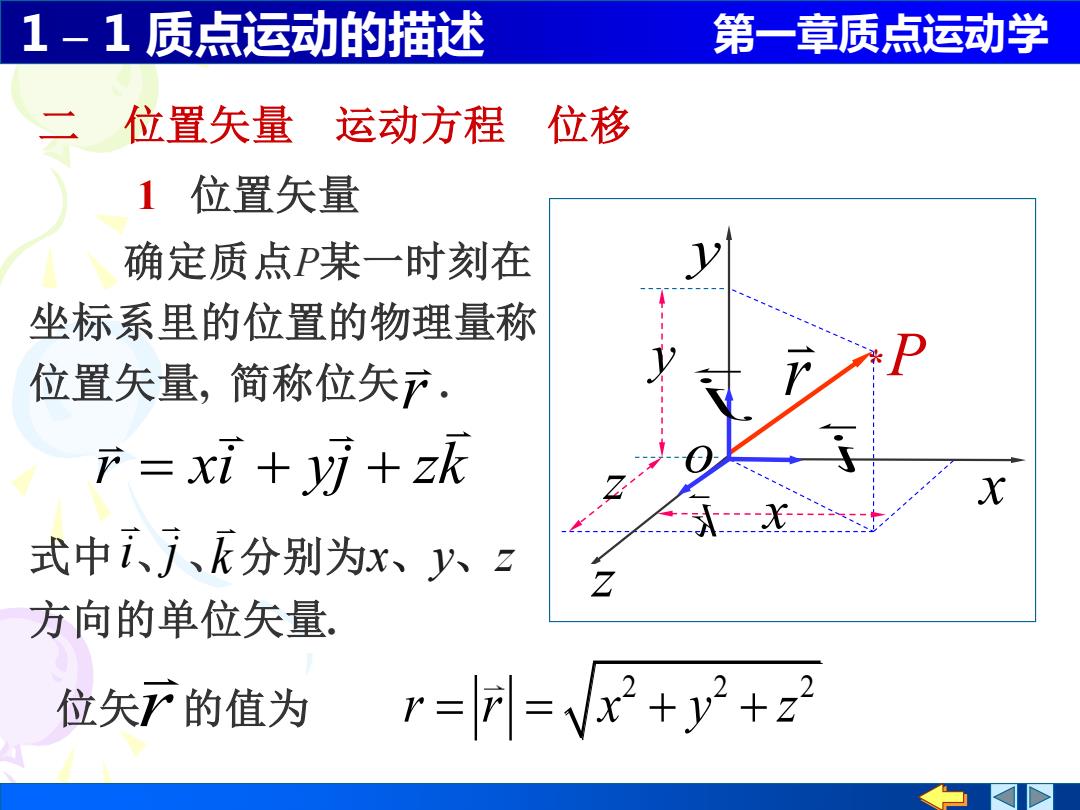
1-1质点运动的描述 第一章质点运动学 位置矢量运动方程 位移 1位置矢量 确定质点P某一时刻在 坐标系里的位置的物理量称 位置矢量,简称位矢下. F=xi+yⅵ+zk 式中i、j、分别为x、y八、2 方向的单位矢量 位矢r的值为 r=|=Vx2+y2+z2
1 – 1 质点运动的描述 第一章质点运动学 二 位置矢量 运动方程 位移 1 位置矢量 r * P x y z x z y o j i k r xi yj zk = + + 2 2 2 位矢 r 的值为 r r x y z = = + + 确定质点P某一时刻在 坐标系里的位置的物理量称 位置矢量, 简称位矢 r . 式中 、 、 分别为x、y、z 方向的单位矢量. i j k
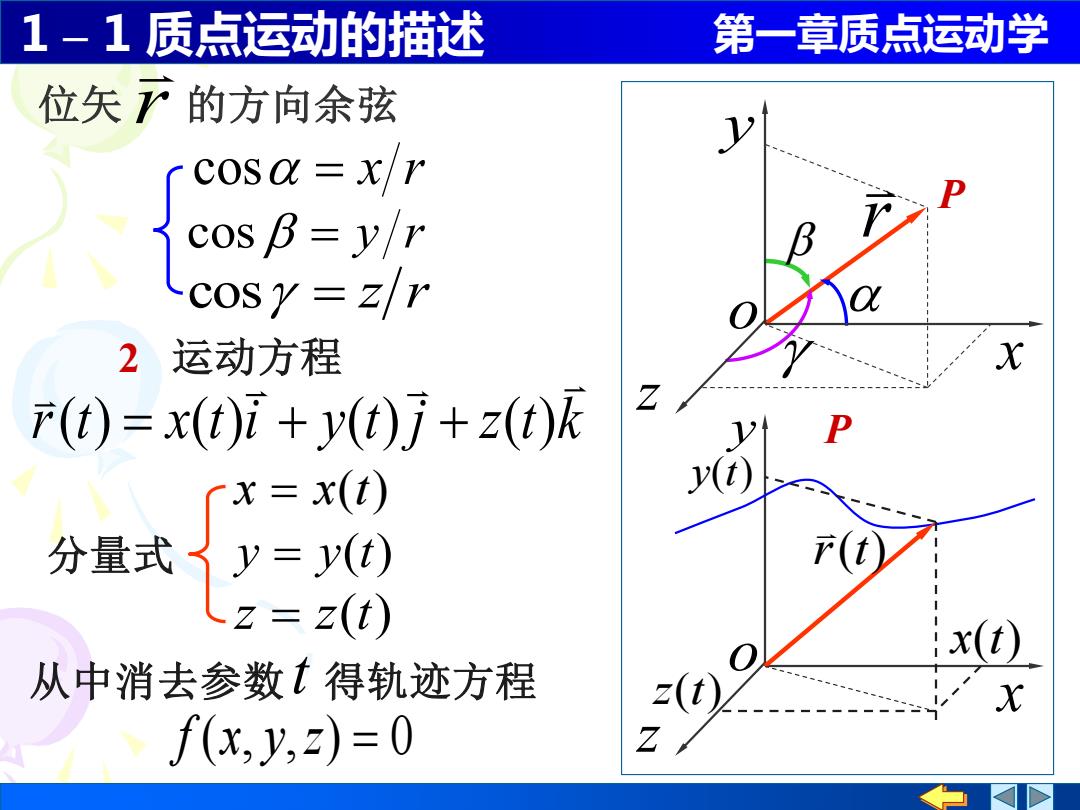
1-1质点运动的描述 第一章质点运动学 位矢下的方向余弦 cosa =x/r cos B=y/r cosy=Z/r 2运动方程 产(t)=x(t)i+y(t)j+z(t)派 「X=x(t) (t) 分量式 y= 、z=z(t) 从中消去参数t得轨迹方程 f(x,y,2)=0
1 – 1 质点运动的描述 第一章质点运动学 cos = x r cos = z r cos = y r 位矢 r 的方向余弦 P P r x z y o x z y o 2 运动方程 r t x t i y t j z t k ( ) = ( ) + ( ) + ( ) x = x(t) y = y(t) z = z(t) 分量式 从中消去参数 得轨迹方程 f (x, y,z) = 0 t r(t) x(t) y(t) z(t)
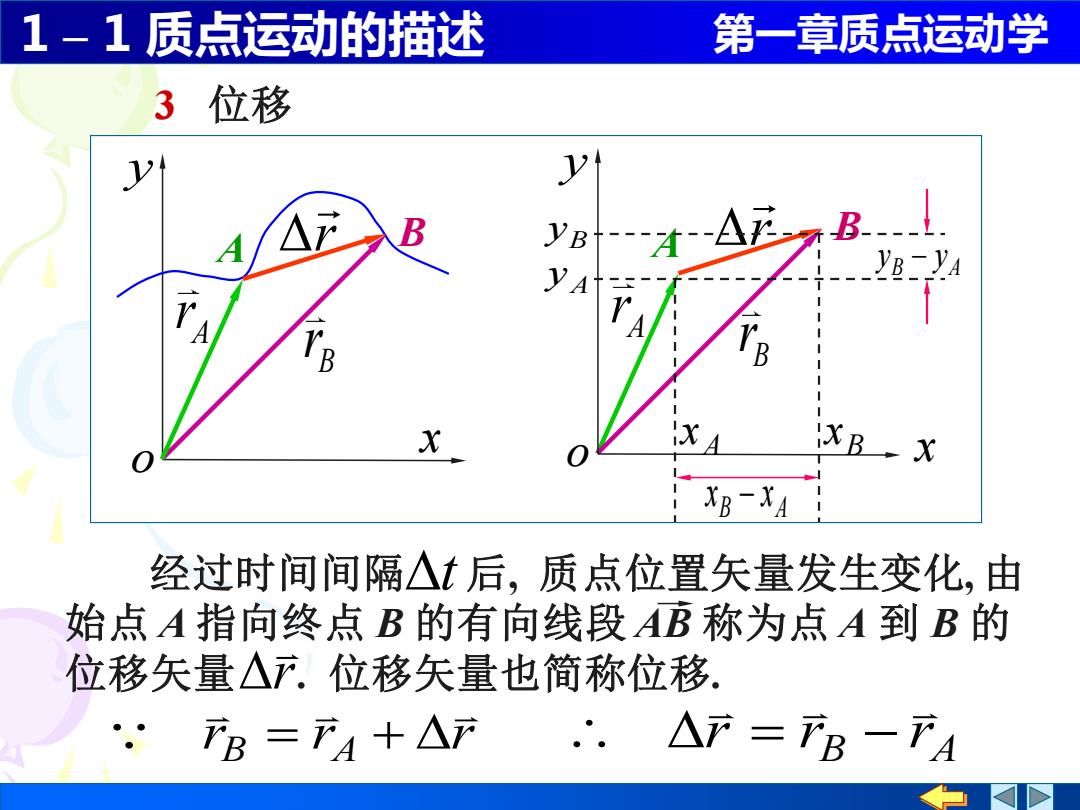
1-1质点运动的描述 第一章质点运动学 3位移 B yB-- yB-YA B X B XR-XA 经过时间间隔△后,质点位置矢量发生变化,由 始点A指向终点B的有向线段AB称为点A到B的 位移矢量△广.位移矢量也简称位 B=产A十△F △产=B一下A
1 – 1 质点运动的描述 第一章质点运动学 3 位移 x y o B B r A r A r A r B B r A r x y o B x A x B A x − x B y A y B A y − y r r r B A = + B A r r r = − 经过时间间隔 后, 质点位置矢量发生变化, 由 始点 A 指向终点 B 的有向线段 AB 称为点 A 到 B 的 位移矢量 . 位移矢量也简称位移. t r
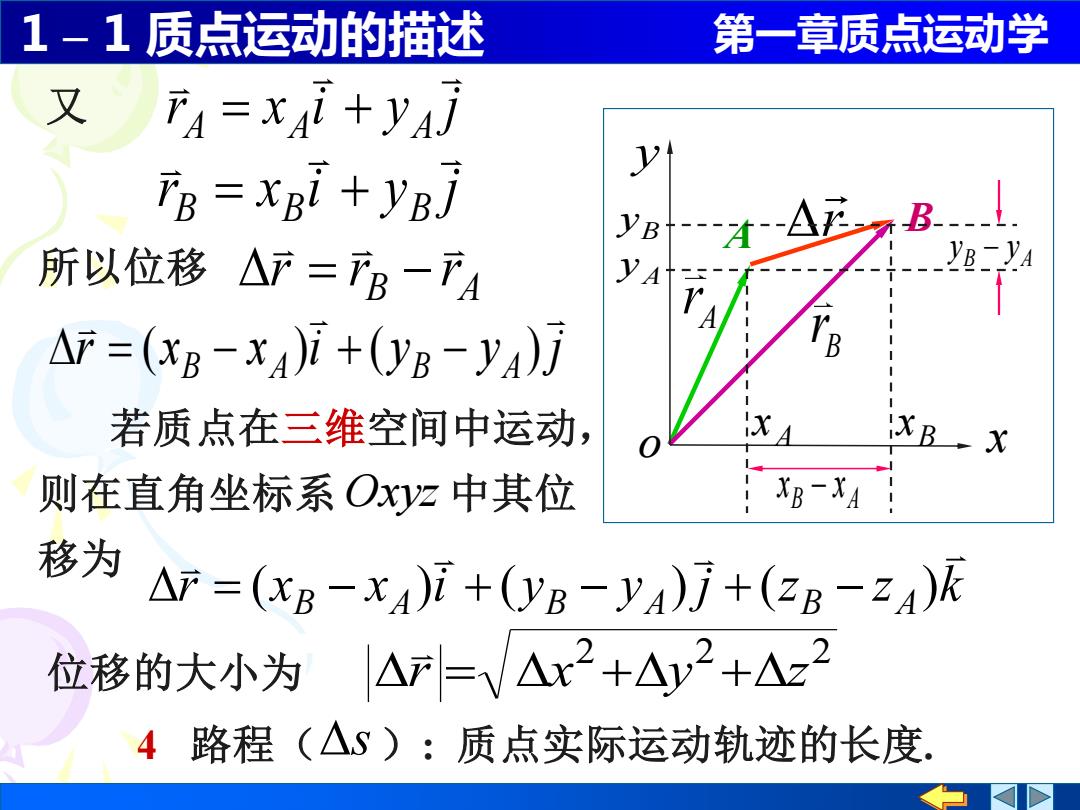
1-1质点运动的描述 第一章质点运动学 又F4=x4i+y4j FB=xBi+yBj 才2 B. 所以位移△产=B一下4 YB-y =(xB-xAi+(yg-yA)月 若质点在三维空间中运动, XBX 则在直角坐标系Oxz中其位 XB-XA 移为△r=(B-x4i+(0yB-yAj+B-21)k 位移的大小为 △F=V△x2+△y2+△z2 4路程(△S):质点实际运动轨迹的长度
1 – 1 质点运动的描述 第一章质点运动学 2 2 2 r = x +y +z 位移的大小为 A r B B r A r x y o B x A x B A x − x B y A y B A y − y r x i y j A A A = + r x i y j B B B = + r x x i y y j B A B A = ( − ) + ( − ) B A r r r 所以位移 = − 若质点在三维空间中运动, 则在直角坐标系 中其位 移为 Oxyz r x x i y y j z z k B A B A B A = ( − ) + ( − ) + ( − ) 4 路程(s ): 质点实际运动轨迹的长度. 又
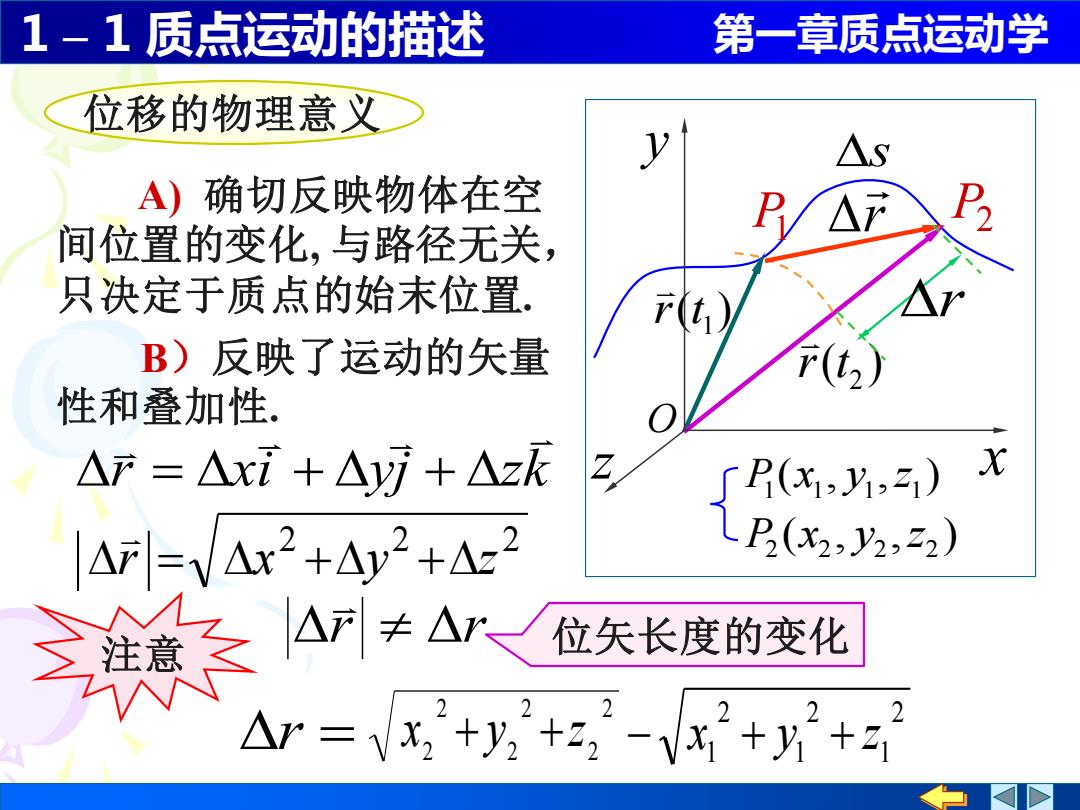
1-1质点运动的描述 第一章质点运动学 位移的物理意义 △S A)确切反映物体在空 △F P 间位置的变化,与路径无关, 只决定于质点的始末位置 B)反映了运动的矢量 性和叠加性. △产=△xi+△i+△2k 了(x,1,) x IAF=VAr2+A2+A-2 P(x2,y2,22) 款Ar交长的型 △=vx,+y+-Vx2+片2+2
1 – 1 质点运动的描述 第一章质点运动学 2 2 2 r = x +y +z r r 2 1 2 1 2 1 − x + y + z 2 2 2 2 2 2 r = x + y +z 位移的物理意义 A) 确切反映物体在空 间位置的变化, 与路径无关, 只决定于质点的始末位置. B)反映了运动的矢量 性和叠加性. s ( , , ) 1 1 1 1 P x y z ( , , ) 2 2 2 2 P x y z ( ) 1 r t P1 ( ) 2 r t r P2 注意 位矢长度的变化 x y O z r r xi yj zk = + +

1-1质点运动的描述 第一章质点运动学 讨论 位移与路程 (A)PP2两点间的路程 是不唯一的,可以是△或△S 而位移人产是唯一的. (B)一般情况,位移 大小不等于路程 △r≠△s (C)什么情况△产=△s? 不改变方向的直线运动;当△t→0时△产=△s· (D)位移是矢量,路程是标量
1 – 1 质点运动的描述 第一章质点运动学 位移与路程 (B) 一般情况, 位移 大小不等于路程. r s (D)位移是矢量, 路程是标量. s ( ) 1 r t 1 p ( ) 2 r t 2 p r x y O z ' s (C)什么情况 r = s ? 不改变方向的直线运动; 当 t → 0 时 r = s . 讨论 (A)P1P2 两点间的路程 是不唯一的, 可以是 或 而位移 r 是唯一的. s ' s
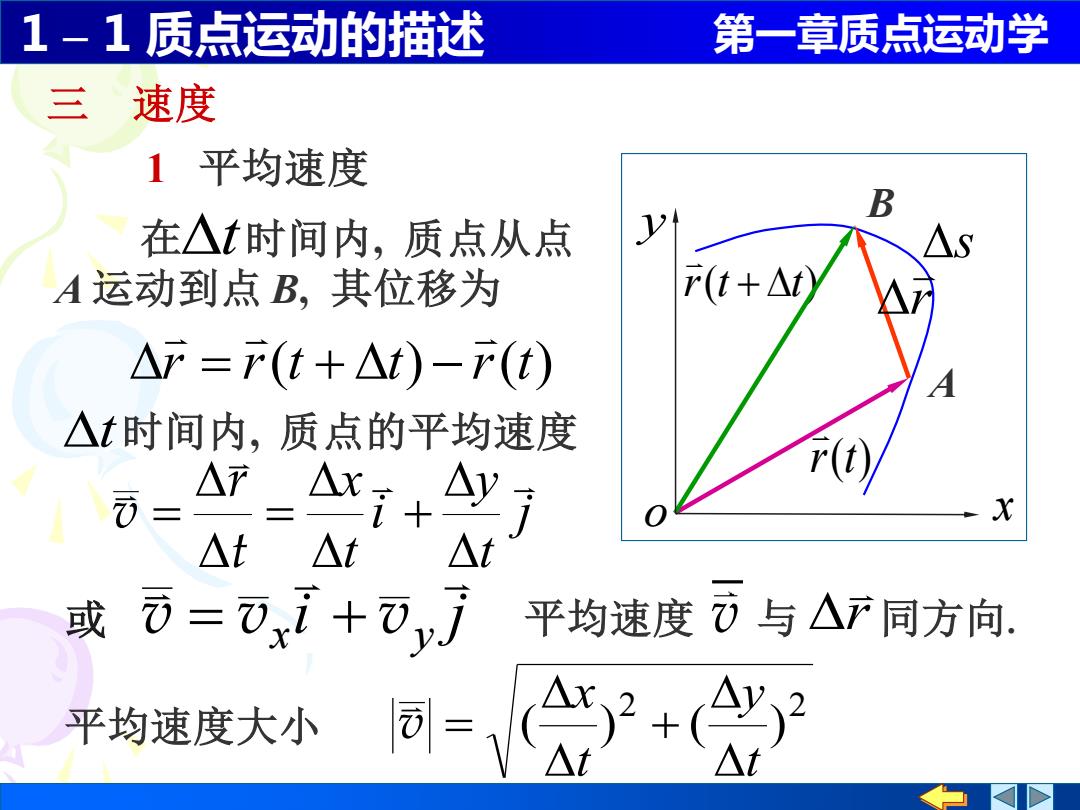
1-1质点运动的描述 第一章质点运动学 三 速度 1平均速度 B 在△时间内,质点从点 A运动到点B,其位移为 r(t+△t) △r=产(t+△t)-r(t) △t时间内,质点的平均速度 △产 △r+ △t △t △t 或ō=⑦xi+)yj 平均速度方与△产同方向. 平均速度大小 同-+y
1 – 1 质点运动的描述 第一章质点运动学 三 速度 1 平均速度 r r(t t) r(t) = + − 在 时间内, 质点从点 A 运动到点 B, 其位移为 t t 时间内, 质点的平均速度 平均速度 与 r 同方向. v j t y i t x + = = t r v 平均速度大小 2 2 ( ) ( ) t y t x + v = i j x y 或 v = v + v r r(t + t) B r(t) A x y o s

1-1质点运动的描述 第一章质点运动学 2瞬时速度 当△t→0时平均速度的极限值叫做瞬时速度, 简称速度 △F dr lim △t>0△t dt lim Axi+1imAy万 产(t) △t->0△t △t-→0△t dr ds F(t+△t) 当△t→0时, ds dt 当质点做曲线运动时,质点在某一点的速度方向 就是沿该点曲线的切线方向
1 – 1 质点运动的描述 第一章质点运动学 2 瞬时速度 当质点做曲线运动时, 质点在某一点的速度方向 就是沿该点曲线的切线方向. 当 时平均速度的极限值叫做瞬时速度, 简称速度 t →0 j t y i t x t t + = →0 →0 v lim lim t r t r t d d lim 0 = = → v dr = ds 当 t → 0 时, t d d e t s v =

1-1质点运动的描述 第一章质点运动学 dt dt ⑦=i+j 若质点在三维空间中运动, 其速度为 dx- dy dt dt ds 瞬时速率:速度)的大小称为速率 e, dt =++告 ds dt
1 – 1 质点运动的描述 第一章质点运动学 x y o v d d d 2 2 2 ( ) ( ) ( ) d d d x y z t t t v v = = + + 瞬时速率:速度 v 的大小称为速率 y v x v i j x y v = v + v j t y i t x d d d d v = + 若质点在三维空间中运动, 其速度为 k t z j t y i t x d d d d d d v = + + d d s t v = t d d e t s v =