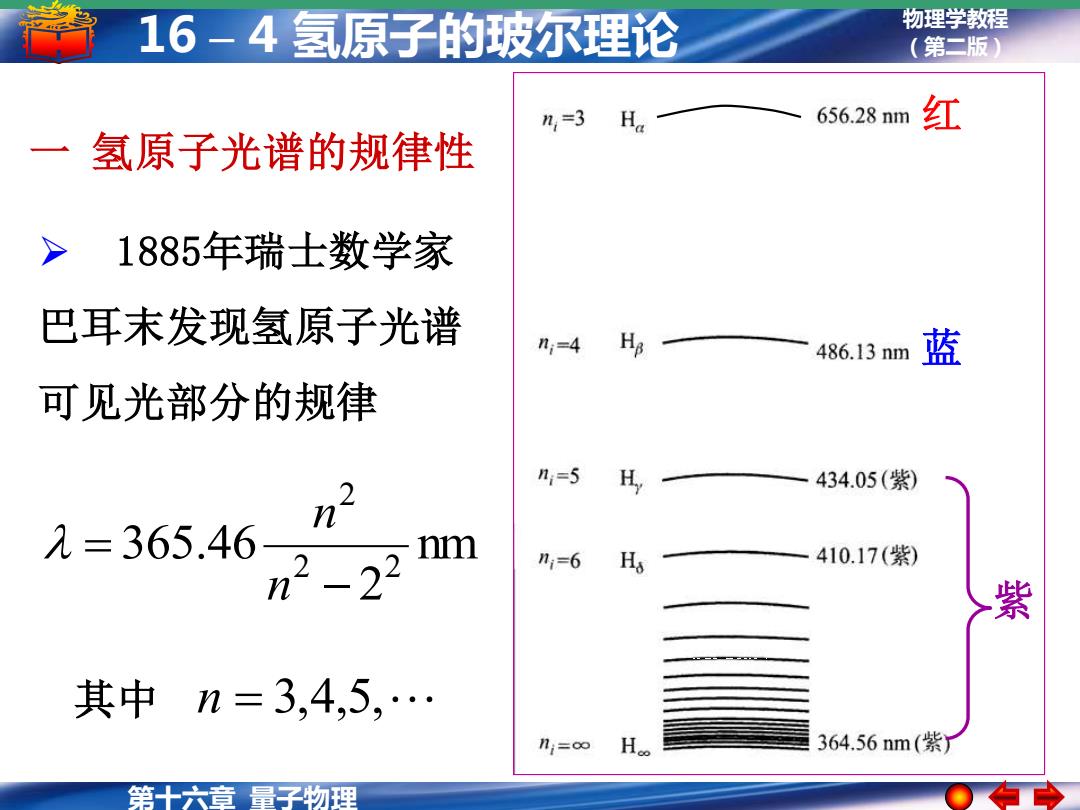
16-4氢原子的玻尔理论 物理学教程 (第二版) n,=3H 656.28nm 红 一 氢原子光谱的规律性 > 1885年瑞士数学家 巴耳末发现氢原子光谱 n,=4 Ha 486.13nm 蓝 可见光部分的规律 n=5 H 434.05(紫) 九=365.46 n2-22 nm n1=6 H 410.17(紫) 其中n=3,4,5,. n;=∞ 364.56nm(紫) 第十六章量子物理
物理学教程 (第二版) 第十六章 量子物理 16 – 4 氢原子的玻尔理论 一 氢原子光谱的规律性 ➢ 1885年瑞士数学家 巴耳末发现氢原子光谱 可见光部分的规律 nm 2 365.46 2 2 2 − = n n 其中 n = 3,4,5, 红 蓝 紫

16-4氢原子的玻尔理论 物理学教程 (第二版 n2 巴耳末公式人=365.46 nm, n=3,4,5,… n2-22 1890年瑞典物理学家里德伯给出氢原子光谱公式 nf=1,2,3,4,…, n,=n+1,nr+2,nr+3,… 里德伯常量 R=1.0973731534x10m 氢原子光谱规律启发人们对原子内部结构的畅想和探索. 第十六章量子物理
物理学教程 (第二版) 第十六章 量子物理 16 – 4 氢原子的玻尔理论 1890 年瑞典物理学家里德伯给出氢原子光谱公式 ) 1 1 ( 1 2 2 nf ni = = R − 波数 里德伯常量 7 1 1.0973731534 10 m − R = nm, 3,4,5, 2 365.46 2 2 2 = − = n n n 巴耳末公式 =1,2,3,4, , nf ni = nf +1,nf + 2,nf + 3, 氢原子光谱规律启发人们对原子内部结构的畅想和探索

16-4氢原子的玻尔理论 物理学教程 (第二版) 紫外 莱曼系 n=2,3,. 1 1 可见光巴尔末系 1n=3,4,… n 1 帕邢系 n=4,5, 1 布拉开系 。n=5,6,… 红外 1 普丰德系o n=6,7,… 汉弗莱系 n=7,82. 第十六章量子物理
物理学教程 (第二版) 第十六章 量子物理 16 – 4 氢原子的玻尔理论 莱曼系 ), 2,3, 1 1 1 ( 1 2 2 = = − n = n R 紫外 ), 3,4, 1 2 1 ( 1 2 2 = = − n = n R 可见光 巴尔末系 ), 4,5, 1 3 1 ( 1 2 2 = = − n = n R 帕邢系 ), 5,6, 1 4 1 ( 1 2 2 = = − n = n R 布拉开系 ), 6,7, 1 5 1 ( 1 2 2 = = − n = n R 普丰德系 ), 7,8, 1 6 1 ( 1 2 2 = = − n = n R 汉弗莱系 红外

16-4氢原子的玻尔理论 物理学教程 (第二版 二卢瑟福的原子有核模型 ◆1897年J.J.汤姆孙发现电子 ◆1903年,汤姆孙提出原子的“葡萄干蛋糕模型” 第一个钻到原子中心的人一卢瑟福 R IS O化粒子散射的仪器 卢瑟福是J.J汤姆孙第一个外国研究生.他开创的 用高速运动粒子作为探针轰击原子,研究原子结构的方 法是核物理和粒子物理实验中最有力的分析方法. 第十六章量子物理
物理学教程 (第二版) 第十六章 量子物理 16 – 4 氢原子的玻尔理论 二 卢瑟福的原子有核模型 1897年 J.J.汤姆孙发现电子 1903年,汤姆孙提出原子的“葡萄干蛋糕模型” 卢瑟福是 J. J.汤姆孙第一个外国研究生. 他开创的 用高速运动粒子作为探针轰击原子,研究原子结构的方 法是核物理和粒子物理实验中最有力的分析方法. 第一个钻到原子中心的人——卢瑟福 粒子散射的仪器 F T P R S

16-4氢原子的玻尔理论 物理学教程 (第二版 卢瑟福学生马斯登和盖革和实验支持了卢瑟福的预言, 粒子散射实验 原子核 1 电子 30 60 120 150 180 对于学生马斯登和盖革所观察到的α粒子大角度 散射,卢瑟福非常兴奋激动地说:“这几乎令人难以 置信,在我的一生中竟会发生这样的事情.如果你将一 颗15英寸的大炮弹射向一张薄纸,炮弹竟然会反射回 来打中你自己! 第十六章量子物理
物理学教程 (第二版) 第十六章 量子物理 16 – 4 氢原子的玻尔理论 原子核 电子 卢瑟福学生马斯登和盖革和实验支持了卢瑟福的预言. 对于学生马斯登和盖革所观察到的α粒子大角度 散射, 卢瑟福非常兴奋激动地说:“这几乎令人难以 置信, 在我的一生中竟会发生这样的事情. 如果你将一 颗 15 英寸的大炮弹射向一张薄纸,炮弹竟然会反射回 来打中你自己!” 粒 子 散 射 实 验

16-4氢原子的玻尔理论 物理学教程 (第二版 卢瑟福提出有核模型: 1.全部正电荷Z集中在原子球体中心,大约占原子 体积几万分之一大小的范围内,构成原子核: 2.原子质量几乎全(99.9%以上)集中于此 3.Z个电子在核外凭借其与正电荷的库仑力做绕核 运动,也就类似于行星那样的运动 卢瑟福的科学态度大胆而谨慎,但他经过深思熟虑, 知道自己所提出的模型很不完善,而且是冒着与经典理 论发生冲突的风险,但他笃信自己的看法有坚实的实验 依据,勇敢地发表出来,不惜向经典物理挑战。卢瑟福 的文章受到大多数同行的冷遇,但玻尔赏识他的文章, 笋十六章量子物理
物理学教程 (第二版) 第十六章 量子物理 16 – 4 氢原子的玻尔理论 ➢ 卢瑟福提出有核模型: 1. 全部正电荷Ze集中在原子球体中心,大约占原子 体积几万分之一大小的范围内,构成原子核. 2. 原子质量几乎全(99.9%以上)集中于此. 3. Z个电子在核外凭借其与正电荷的库仑力做绕核 运动,也就类似于行星那样的运动. 卢瑟福的科学态度大胆而谨慎,但他经过深思熟虑, 知道自己所提出的模型很不完善,而且是冒着与经典理 论发生冲突的风险,但他笃信自己的看法有坚实的实验 依据,勇敢地发表出来,不惜向经典物理挑战。卢瑟福 的文章受到大多数同行的冷遇,但玻尔赏识他的文章
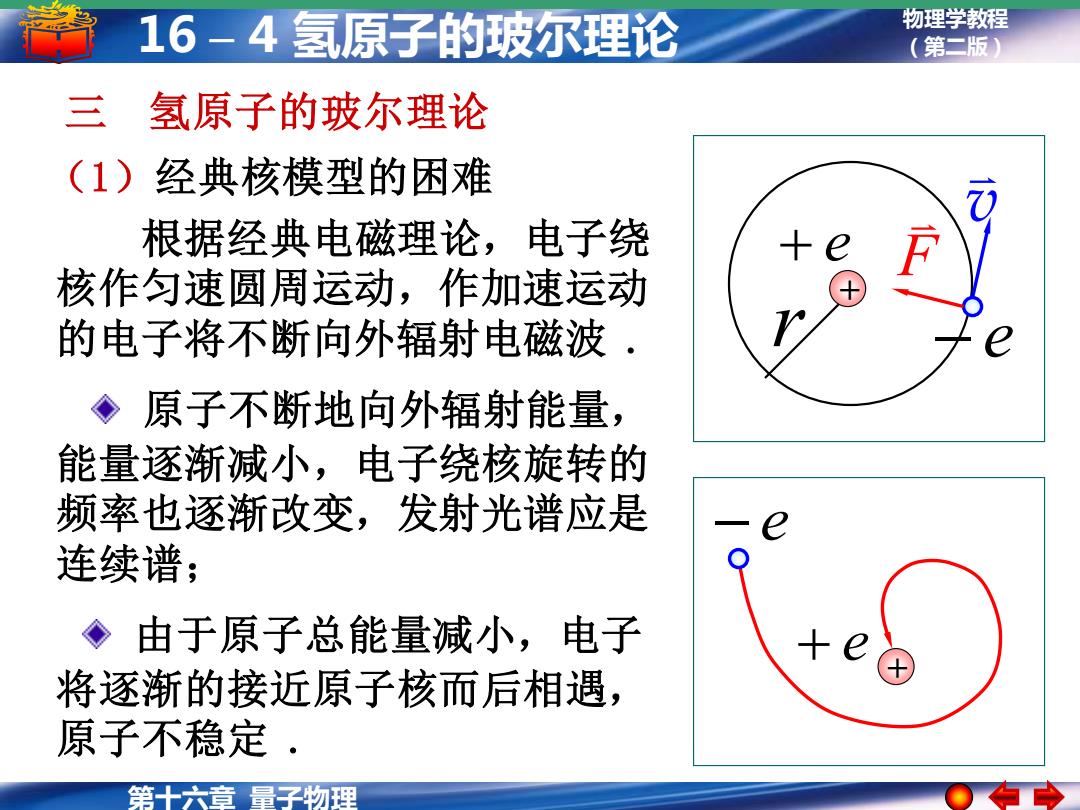
16-4氢原子的玻尔理论 物理学教程 (第二版 三 氢原子的玻尔理论 (1)经典核模型的因难 根据经典电磁理论,电子绕 十 核作匀速圆周运动,作加速运动 的电子将不断向外辐射电磁波 , ◆原子不断地向外辐射能量, 能量逐渐减小,电子绕核旋转的 频率也逐渐改变,发射光谱应是 连续谱; ◆由于原子总能量减小,电子 将逐渐的接近原子核而后相遇, 原子不稳定 。 第十六章量子物理
物理学教程 (第二版) 第十六章 量子物理 16 – 4 氢原子的玻尔理论 三 氢原子的玻尔理论 (1)经典核模型的困难 根据经典电磁理论,电子绕 核作匀速圆周运动,作加速运动 的电子将不断向外辐射电磁波 . v F r − e + e + 原子不断地向外辐射能量, 能量逐渐减小,电子绕核旋转的 频率也逐渐改变,发射光谱应是 连续谱; 由于原子总能量减小,电子 将逐渐的接近原子核而后相遇, 原子不稳定 . − e + + e

16-4氢原子的玻尔理论 物理学教程 (第二版) (2)玻尔的三个假设 假设一电子在原子中,可以在一些特定的轨道上 运动而不辐射电磁波,这时原子处于稳定状态(定态), 并具有一定的能量. 假设二电子以速度)在半径为?的圆周上绕核运 动时,只有电子的角动量L等于/2元的整数倍的那些 轨道是稳定的· h 量子化条件L=mor=n 主量子数 2元 n=1,2,3, 假设三 当原子从高能量 E,的定态跃迁到低能量 E 的定态时,要发射频率为V的光子 频率条件 hv=E,-E 第十六章量子物理
物理学教程 (第二版) 第十六章 量子物理 16 – 4 氢原子的玻尔理论 (2)玻尔的三个假设 假设一 电子在原子中,可以在一些特定的轨道上 运动而不辐射电磁波,这时原子处于稳定状态(定态), 并具有一定的能量. 2π h 量子化条件 L = mvr = n 频率条件 h = Ei − Ef 假设二 电子以速度 在半径为 的圆周上绕核运 动时,只有电子的角动量 等于 的整数倍的那些 轨道是稳定的 . h 2π v r L 主量子数 n =1,2,3, 假设三 当原子从高能量 Ei 的定态跃迁到低能量 Ef 的定态时,要发射频率为 的光子

16-4氢原子的玻尔理论 物理学教程 (第二版) 氢原子能级公式 己2 n 由牛顿定律 =n 4π8orm 2 h 由假设2量子化条件mUnn=n 2元 Eoh2 In 2 n2=rn2(n=1,2,3,) 元me n=1,玻尔半径= &h2 =5.29×101lm πmei 1 2 第n轨道电子总能量 E= -mu 4元8o'n 第十六章量子物理
物理学教程 (第二版) 第十六章 量子物理 16 – 4 氢原子的玻尔理论 2 1 2 2 2 0 π n r n me h rn = = (n =1,2,3, ) 2π h 由假设 2 量子化条件 mvn rn = n n n n r m r e 2 2 0 2 4π v = 由牛顿定律 , 玻尔半径 5.29 10 m π 1 1 2 2 0 1 − = = me h r n =1 氢原子能级公式 n n n n r e E m 0 2 2 2 4π 1 第 轨道电子总能量 = v −

16-4氢原子的玻尔理论 物理学教程 (第二版) 1 e En= 自由态 氢原子能级图 n 2 An 8on E/eV me4 n=00 1 E 0 En n2 激发态 n= ===-0.85 8coh2 n=. -----1.51 基态能量 (n=1) n=2 ----3.4 E me4 8soh2 13.6eV(电离能) 激发态能量(n>1) En=E/n2 基态n=1---13.6 第十六章量子物理
物理学教程 (第二版) 第十六章 量子物理 16 – 4 氢原子的玻尔理论 基态能量 2 2 0 4 1 8 h me E = − = −13.6eV(n =1) 2 1 2 2 2 0 4 1 8 n E h n me En = − = n n n r e E m 0 2 2 2 4π 1 = v − (电离能) 2 En = E1 n 激发态能量 (n 1) E/ eV 氢原子能级图 基态 n =1 −13.6 n = 2 n = 3 激 n = 4 发 态 −3.4 −1.51 −0.85 n = 0 自 由 态