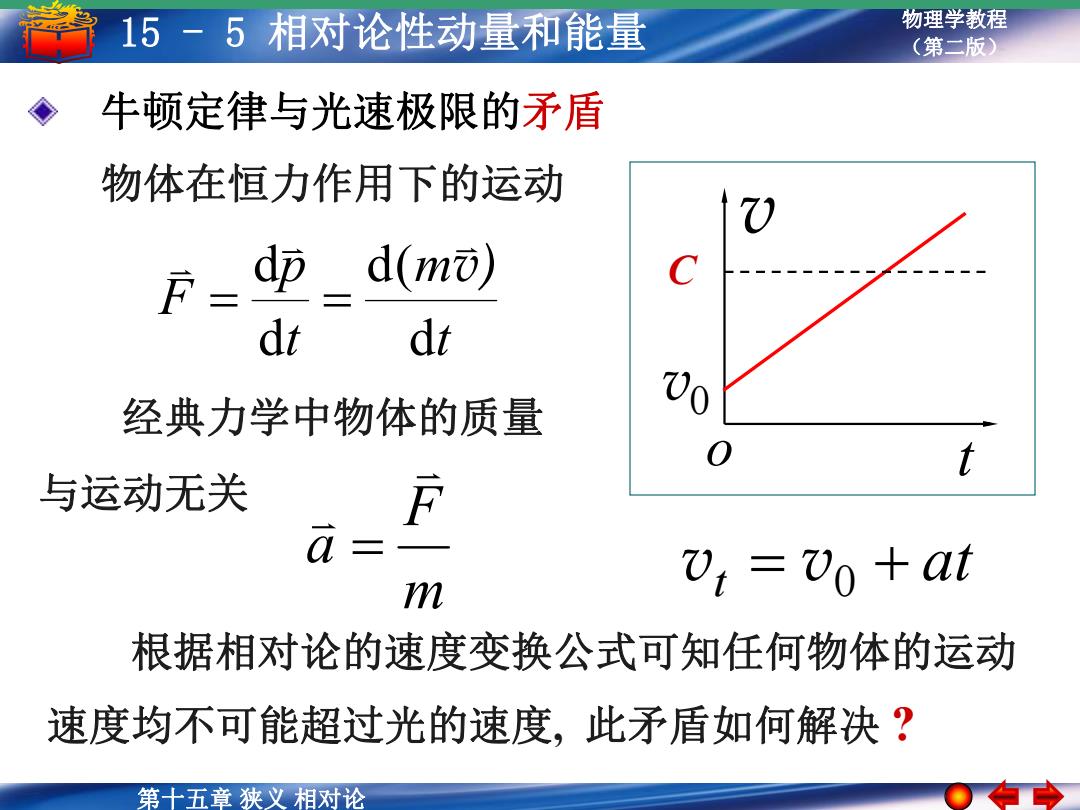
15-5相对论性动量和能量 物理学教程 (第二版) 牛顿定律与光速极限的矛盾 物体在恒力作用下的运动 ) dp d(mi) dt dt 经典力学中物体的质量 0 与运动无关 F a= m 7:=7o +at 根据相对论的速度变换公式可知任何物体的运动 速度均不可能超过光的速度,此矛盾如何解决? 第十五章狭义相对论
第十八章狭义 相对论 第十五章 狭义 相对论 物理学教程 15 - 5 相对论性动量和能量 (第二版) 牛顿定律与光速极限的矛盾 t v C 0 v o t m t p F d d( d d v) 物体在恒力作用下的运动 at vt v0 m F a 经典力学中物体的质量 与运动无关 根据相对论的速度变换公式可知任何物体的运动 速度均不可能超过光的速度, 此矛盾如何解决 ?

15-5相对论性动量和能量 物理学教程 (第二版) 动量与速度的关系 按照狭义相对论原理和洛伦兹变换的要求 1)相对论动量万= B=moo-mo mov 当)<<C时 p=mō→mo) mo 2)相对论质量 m= V1-B2 mo m()在不同惯性系中大小不同. 静质量m,:物体相对于惯性系静止时的质量 第十五章狭义相对论
第十八章狭义 相对论 第十五章 狭义 相对论 物理学教程 15 - 5 相对论性动量和能量 (第二版) 1)相对论动量 v v v m m m p 0 2 0 1 当 v c 时 v v m m0 p 一 动量与速度的关系 2)相对论质量 2 0 1 m m 静质量m0 :物体相对于惯性系静止时的质量 . m(v) 在不同惯性系中大小不同 . v m C m0 o 按照狭义相对论原理和洛伦兹变换的要求
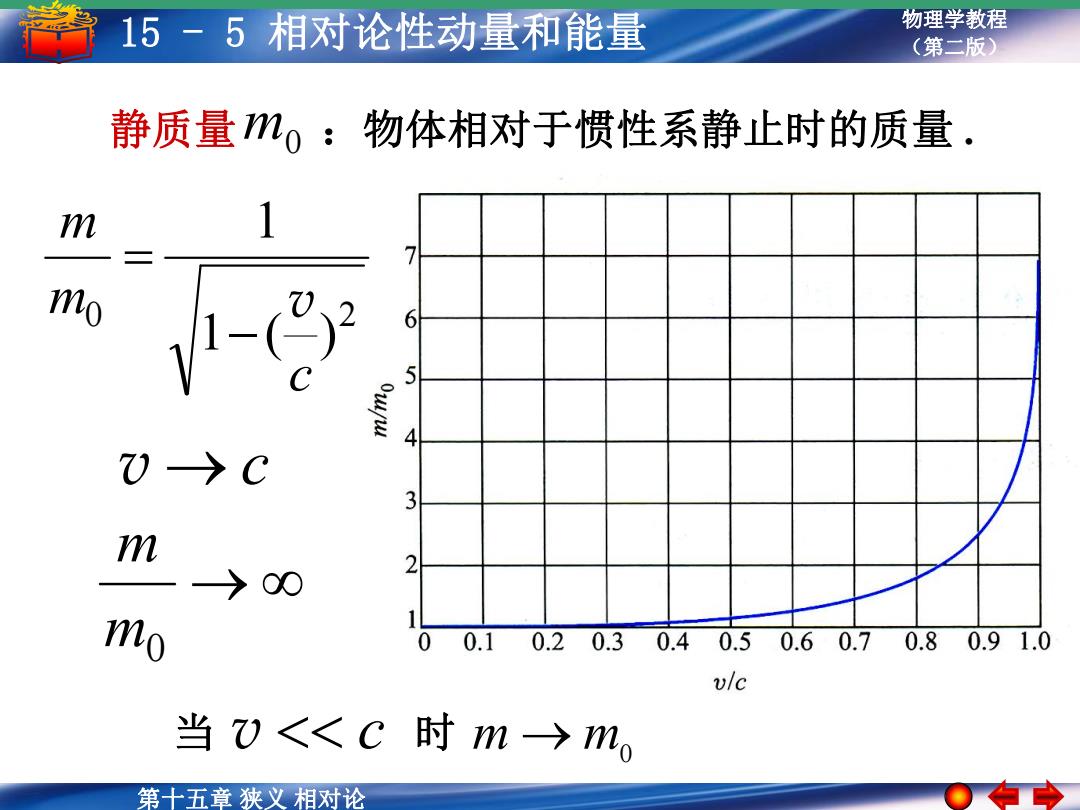
15-5相对论性动量和能量 物理学教程 (第二版) 静质量mo:物体相对于惯性系静止时的质量. mo 7 )〉C m >00 mo 00.10.20.30.40.50.60.70.80.91.0 vlc 当)<<C时m-→m, 第十五章狭义相对论
第十八章狭义 相对论 第十五章 狭义 相对论 物理学教程 15 - 5 相对论性动量和能量 (第二版) 0 2 1 ( ) 1 c m m v 静质量m0 :物体相对于惯性系静止时的质量 . 当 v c 时 m m0 v c m0 m

15-5相对论性动量和能量 物理学教程 (第二版) 二 狭义相对论力学的基本方程 dp mo⑦ d市 dm dt dr dt 当v→c时,dm/dt急剧增加, 而a→>0,所以光速C为物体的极限速度. 当)mo d F=m dt 第十五章狭义相对论
第十八章狭义 相对论 第十五章 狭义 相对论 物理学教程 15 - 5 相对论性动量和能量 (第二版) 二 狭义相对论力学的基本方程 ) 1 ( d d d d 2 0 v m t t p F t m t m d d d d v v 当 时, 急剧增加 , 而 ,所以光速 C 为物体的极限速度 . v c dm dt a 0 m m0 当 v c 时 m a t F m 0 d d v

15-5相对论性动量和能量 物理学教程 (第二版) 相对论动量守恒定律 ∑F,=0时 当 =常矢量 若)<<C,则相对论动量守恒◆经典动量守恒. Σ%2又 五音独议相对论
第十八章狭义 相对论 第十五章 狭义 相对论 物理学教程 15 - 5 相对论性动量和能量 (第二版) 相对论动量守恒定律 0 i Fi 当 时 常矢量 i i i i i m p 2 0 1 v 常矢量 i i i i i i i i m m p v v 0 2 0 1 若 v c ,则相对论动量守恒 经典动量守恒

15-5相对论性动量和能量 物理学教程 (第二版) 三 质量与能量的关系 相对论质能关系 E=mc2=moc2+Es 静能m,c2:物体静止时所具有的能量. 质能关系预言:物质的质量就是能量的一种储藏. 爱因斯坦认为(1905) 懒惰性→惯性(inertia) 物体的懒惰性就 活泼性→能量(energy) 是物体活泼性的度量. > 相对论能量和质量守恒是一个统一的物理规律, 第十五章狭义相对论
第十八章狭义 相对论 第十五章 狭义 相对论 物理学教程 15 - 5 相对论性动量和能量 (第二版) 三 质量与能量的关系 k 2 0 2 Ø 相对论质能关系 E mc m c E Ø 静能 :物体静止时所具有的能量 . 2 0 m c 质能关系预言:物质的质量就是能量的一种储藏 . 爱因斯坦认为(1905) 懒惰性 惯性 ( inertia ) 活泼性 能量 ( energy ) 物体的懒惰性就 是物体活泼性的度量 . Ø 相对论能量和质量守恒是一个统一的物理规律
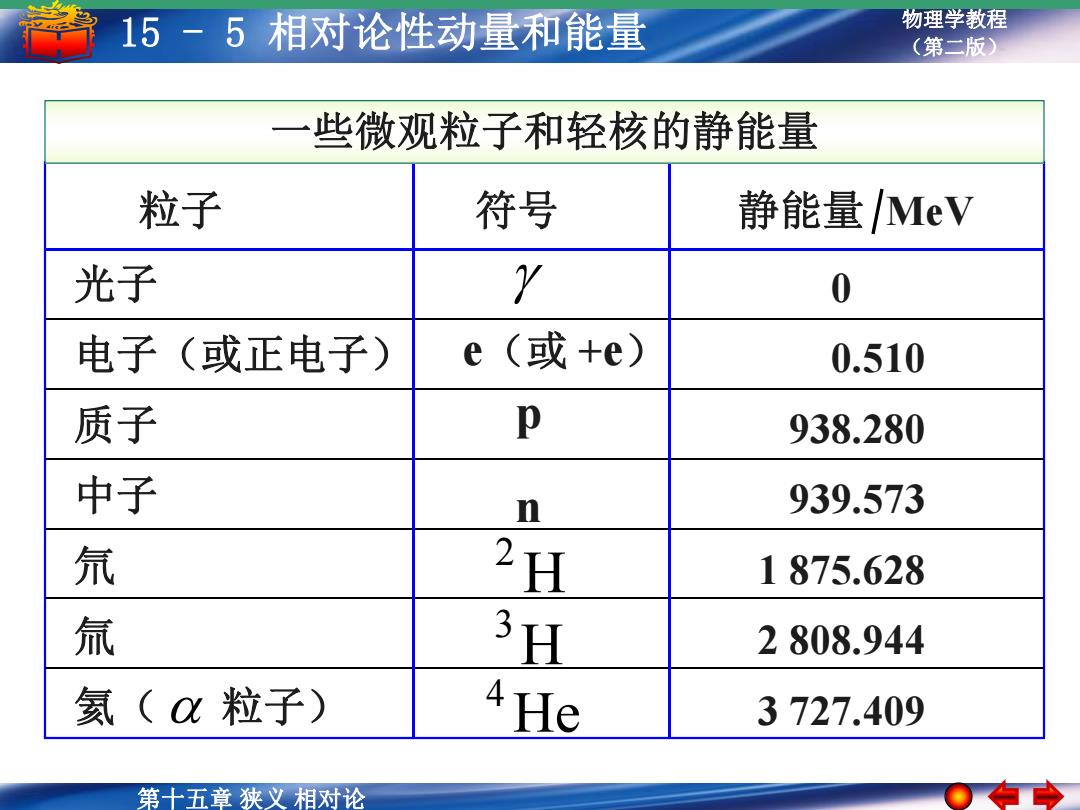
15-5相对论性动量和能量 物理学教程 (第二版) 一 些微观粒子和轻核的静能量 粒子 符号 静能量MeV 光子 Y 0 电子(或正电子) e(或+e) 0.510 质子 p 938.280 中子 n 939.573 氘 2H 1875.628 氘 3H 2808.944 氦(粒子) 4He 3727.409 第十五章狭义相对论
第十八章狭义 相对论 第十五章 狭义 相对论 物理学教程 15 - 5 相对论性动量和能量 (第二版) 一些微观粒子和轻核的静能量 粒子 符号 静能量 MeV 光子 电子(或正电子) 质子 中子 氘 氚 氦( 粒子) 0 0.510 938.280 939.573 1 875.628 2 808.944 3 727.409 e(或 +e) p n H 2 H 3 He 4

15-5相对论性动量和能量 物理学教程 (第二版) 物理意义 100 JAHRE RELATIVITAT-ATOME -QUANTEN 55 E=mc2 =mc2 △E=(Am)c2 00 惯性质量的增加和能量的增加相联系,质量的 大小应标志着能量的大小,这是相对论的又一极其 重要的推论. 相对论的质能关系为开创原子能时代提供了理 论基础,这是一个具有划时代的意义的理论公式. 第十五章狭义相对论
第十八章狭义 相对论 第十五章 狭义 相对论 物理学教程 15 - 5 相对论性动量和能量 (第二版) 物理意义 2 E mc 2 E (m)c 惯性质量的增加和能量的增加相联系,质量的 大小应标志着能量的大小,这是相对论的又一极其 重要的推论 . 相对论的质能关系为开创原子能时代提供了理 论基础 , 这是一个具有划时代的意义的理论公式

15-5相对论性动量和能量 物理学教程 (第二版) 质能关系预言:物质的质量就是能量的一种储藏 例:=1kg,E=mc2=9×1016J 现有100座楼,每楼200套房,每套房用电功率 10000W,总功率2×108W,每天用电10小时, 年耗电量2.72×1015J,可用约33年。 1千克汽油的燃烧值为4.6×107焦耳. 例如,1kg水由0°C加热到100°C时所增加的 能量为 △E=4.18×103×100J=4.18×105J 质量增加 △m=△Ec2=4.6×10-12kg 第十五章狭义相对论
第十八章狭义 相对论 第十五章 狭义 相对论 物理学教程 15 - 5 相对论性动量和能量 (第二版) 例: 1kg, 9 10 J 2 16 m0 E0 m0c 现有 100 座楼,每楼 200 套房,每套房用电功率 10000 W , 总功率 ,每天用电 10 小时 , 年耗电量 ,可用约 33 年。 210 8W 2.72 10 J 15 质能关系预言:物质的质量就是能量的一种储藏. 1千克汽油的燃烧值为 焦耳 . 7 4.610 例如,1kg 水由 0 加热到 100 时所增加的 能量为 4.18 10 100J 4.18 10 J 3 5 E 质量增加 4.6 10 kg 2 12 m E c C C

15-5相对论性动量和能量 物理学教程 (第二版) *四质能公式在原子核裂变和聚变中的应用 1核裂变 25U+6n→9Xe+38r+26n 质量亏损 △m=0.22u 原子质量单位 1u=1.66×10-27kg 放出的能量 Q=△E=(Am)c2≈200MeV 1g轴-235的原子裂变所释放的能量 2=8.5×1010J 第十五章狭义相对论
第十八章狭义 相对论 第十五章 狭义 相对论 物理学教程 15 - 5 相对论性动量和能量 (第二版) * 四 质能公式在原子核裂变和聚变中的应用 U n Xe Sr 2 n 1 0 95 38 139 54 1 0 235 92 质量亏损 m 0.22 u 原子质量单位 1u 1.66 10 kg 27 放出的能量 ( ) 200MeV 2 Q E m c 1g 铀- 235 的原子裂变所释放的能量 8.5 10 J 10 Q 1 核裂变