
14-2扬氏双缝干涉实验 光程劳埃德镜 物理学教程 (第二版) 杨氏双缝干涉实验 B 实验装置 x d'>>d sin0≈tan0=x/d' 波程差 Ar=5-r≈dsin0=d d' 第十四章波动光学
第十四章 波动光学 物理学教程 14 – 2 杨氏双缝干涉实验 光程 劳埃德镜 (第二版) s x o o B 实 验 装 置 d 1 s 2 s 1 r 2 r d' d d' x = d 一 杨氏双缝干涉实验 d' r 波程差 r = r2 − r1 d sin sin tan = x d

14-2杨氏双缝干涉实验 光程 劳埃德镜 物理学教程 (第二版) ±kλ 加强 k=0,1,2, 减弱 士k 明纹 k=0,1,2,· 2+月 d 暗纹 第十四章波动光
第十四章 波动光学 物理学教程 14 – 2 杨氏双缝干涉实验 光程 劳埃德镜 (第二版) 2 (2 1) k + 减弱 k = = d' x r d 加强 k = 0,1,2, 2 (2 1) ' k + d d 暗纹 d d k ' x = 明纹 k = 0,1,2, p 1 s 2 s s x o o B d 1 r 2 r d' r

14-2杨氏双缝干涉实验 光程劳埃德镜 物理学教程 (第二版) 明暗条纹的位置 d' ±士k d 明纹 k=0,1,2, 暗纹 白光照射时,出现彩色条纹 d'入 讨论 条纹间距 △x (△k=1) d 1) 条纹间距与九的关系;d、d'一定时, 若入变化,则△x将怎样变化? 第十四章波动光学
第十四章 波动光学 物理学教程 14 – 2 杨氏双缝干涉实验 光程 劳埃德镜 (第二版) 讨论 条纹间距 (k =1) d d x ' = 白光照射时,出现彩色条纹 ➢ 明暗条纹的位置 2 (2 1) ' k + d d 暗纹 x = d d k ' 明纹 k = 0,1,2, 1)条纹间距 与 的关系 ; 若 变化 ,则x 将怎样变化?d、d' 一定时,
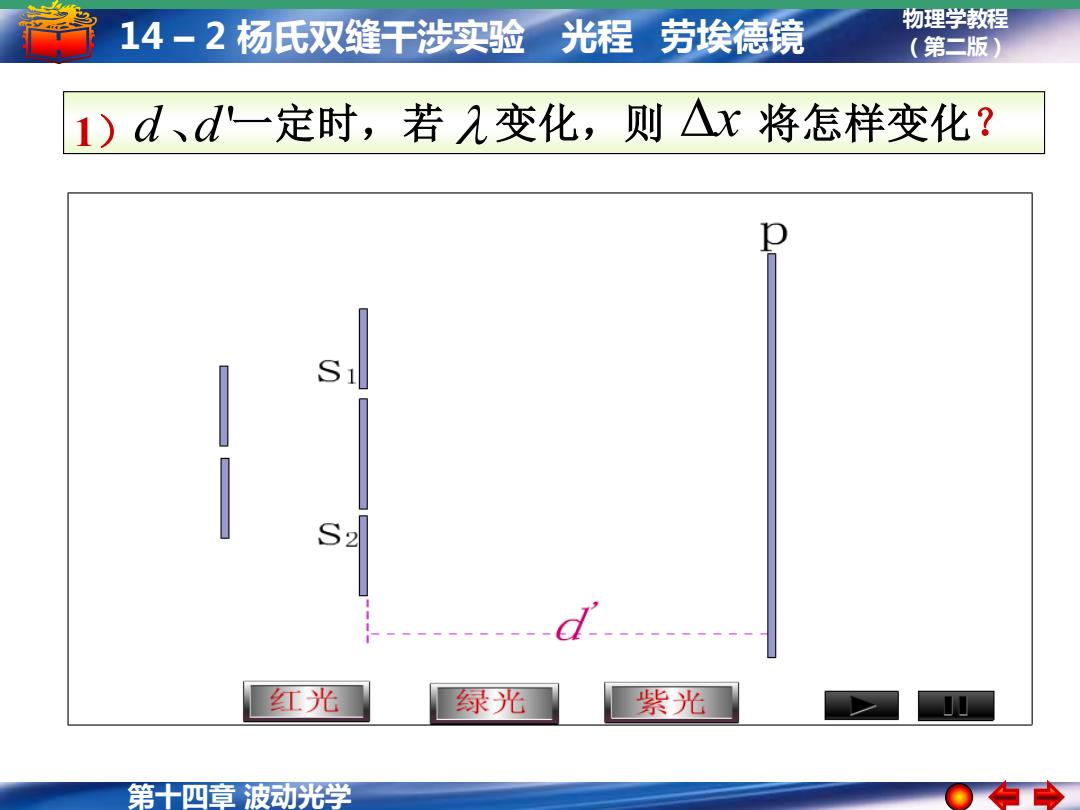
14-2杨氏双缝干涉实验 光程 劳埃德镜 物理学教程 (第二版) 1)d、d一定时,若几变化,则△x将怎样变化? 红光 绿光 紫光 第十四章波动光学
第十四章 波动光学 物理学教程 14 – 2 杨氏双缝干涉实验 光程 劳埃德镜 (第二版) 1) d、d' 一定时,若 变化,则 x 将怎样变化?

14-2杨氏双缝干涉实验 光程劳埃德镜 物理学教程 (第二版) 2)入、d'一定时,条纹间距△与d的关系如何? 缝间距变小 缝间距变大 第十四章波动光学
第十四章 波动光学 物理学教程 14 – 2 杨氏双缝干涉实验 光程 劳埃德镜 (第二版) 2) 、d' 一定时,条纹间距 x 与 d 的关系如何?

14-2杨氏双缝干涉实验 光程 劳埃德镜 物理学教程 (第二版) 例1以单色光照射到相距为0.2mm的双缝上,双缝与 屏幕的垂直距离为10m ()若屏上第一级干涉明纹到同侧的第四级明纹中 心间的距离为75mm,求单色光的波长; (2)若入射光的波长为600nm,求相邻两暗纹中心间的 距离 解: D4=±.k=0.L2, △x4=x4-x1=d'(k4-k)2/d 元=△x4d/[d'(k4-k力=500m (2) △x=d'/(d2)=30mm 第十四章波动光学
第十四章 波动光学 物理学教程 14 – 2 杨氏双缝干涉实验 光程 劳埃德镜 (第二版) 例1 以单色光照射到相距为0.2mm的双缝上,双缝与 屏幕的垂直距离为10m. (1) 若屏上第一级干涉明 纹 到同侧 的第四级明纹中 心间的距离为75mm,求单色光的波长; (2) 若入射光的波长为600nm,求相邻两暗纹中心间的 距离. 解:(1) , = 0,1,2, = k k d d xk x14 = x4 − x1 = d(k4 −k1 ) d = x14d [d(k4 −k1 )] = 500nm (2) x = d (d) = 30mm
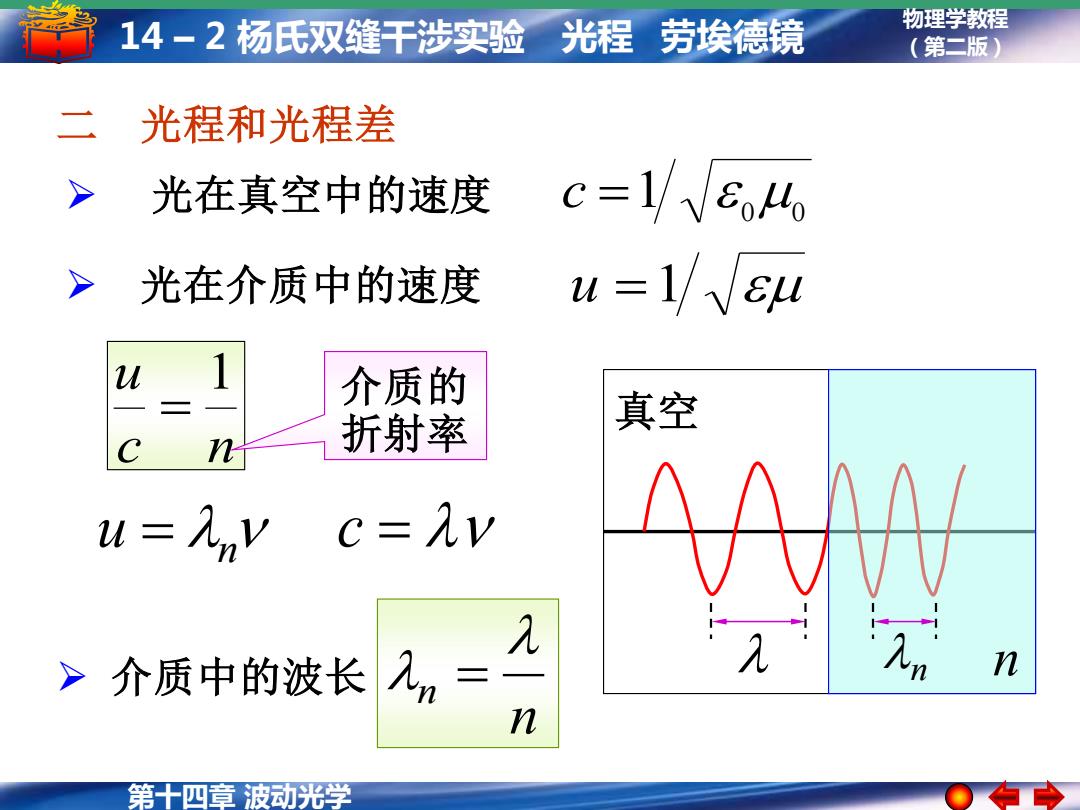
14-2扬氏双缝干涉实验 光程劳埃德镜 物理学教程 (第二版) 二 光程和光程差 光在真空中的速度 c=1/V64 光在介质中的速度 u =1su 介质的 折射率 真空 n u=人n ,c=λy >介质中的波长 m= n 第十四章波动光学
第十四章 波动光学 物理学教程 14 – 2 杨氏双缝干涉实验 光程 劳埃德镜 (第二版) 二 光程和光程差 ➢ 光在真空中的速度 1 0 0 c = ➢ 光在介质中的速度 u =1 c n u 1 = u = n c = n n ➢ 介质中的波长 = 介质的 折射率 n n 真空

14-2杨氏双缝干涉实验 光程 劳埃德镜 物理学教程 (第二版) 问如图两相干光源光振 S1 r 动相位相同,且=,,P 点干涉加强还是减弱? S2*1r2 问:若将这两光源置于右 S1太 图的介质中,P点干涉结果是 否变化? S2* n 两光源的光波在 E=Exo cos2r( P点的光振动方程 E2=E20c0s2π(7 第十四章波动光学
第十四章 波动光学 物理学教程 14 – 2 杨氏双缝干涉实验 光程 劳埃德镜 (第二版) * 1 s P 1 r * 2 s 2 r * 1 s P 1 r * 2 s 2 r n 问: 若将这两光源置于右 图的介质中, P 点干涉结果是 否变化 ? cos 2π ( ) 1 1 1 0 r T t E = E − cos 2π( ) 2 2 2 0 n r T t E E = − 两光源的光波在 P 点的光振动方程 问 如图两相干光源光振 动相位相同,且 , P 点干涉加强还是减弱 ? 1 2 r = r

14-2扬氏双缝干涉实验 光程劳埃德镜 物理学教程 (第二版) >介质中的波长 n= S1 >波程差 △=2- S2* n >相位差 ap=221-2》 =2a-=-2x(57) 1)光程:媒质折射率与光的几何路程之积=n严 物理意义:光程就是光在媒质中通 nr 过的几何路程,按波数相等折合到真空 中的路程。 第十四章波动光学
第十四章 波动光学 物理学教程 14 – 2 杨氏双缝干涉实验 光程 劳埃德镜 (第二版) ➢ 波程差 2 1 r = r − r ➢ 相位差 2π( ) 2π( ) 2 1 r T r t T t n = − − − 2π( ) 2 1 r r n = − − 2π ( ) 2 1 nr − r = − 物理意义:光程就是光在媒质中通 过的几何路程 , 按波数相等折合到真空 中的路程. r nr n = 1) 光程: 媒质折射率与光的几何路程之积 = nr * 1 s P 1 * r 2 s 2 r n n n ➢ 介质中的波长 =

14-2杨氏双缝干涉实验 光程 劳埃德镜 物理学教程 (第二版) 2)光程差(两光程之差) S1* 光程差△=nr- 相位差A0=2元 S2* n >Ts如公。+经发00品2 >干涉减弱 4=2k+10分=0.1,2 A0=±(2k+1元,k=01,2, 第十四章波动光学
第十四章 波动光学 物理学教程 14 – 2 杨氏双缝干涉实验 光程 劳埃德镜 (第二版) 2)光程差 (两光程之差) 2 1 光程差 Δ = nr − r Δ = k, k = 0,1,2, = 2kπ ,k = 0,1,2, ➢ 干涉加强 λ Δ 2π Δ 相位差 = ➢ 干涉减弱 , 0,1,2, 2 Δ = (2k +1) k = = (2k +1)π ,k = 0,1,2, * 1 s P 1 * r 2 s 2 r n