14-9光的偏振性马吕斯定律 物理学教程 (第二版) 光的波动性 光的干涉、衍射. 光波是横波 光的偏振. 机械横波与纵波的区别 机械波穿过狭缝 第十四章波动光学
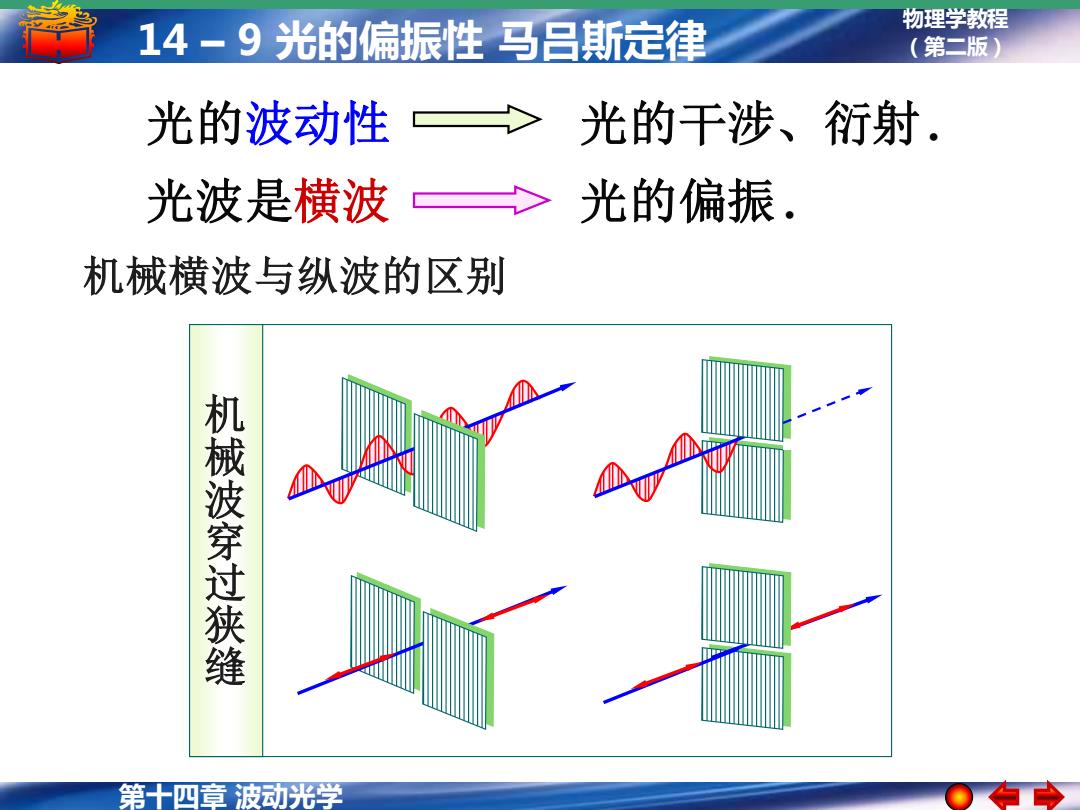
第十四章 波动光学 物理学教程 14 – 9 光的偏振性 马吕斯定律 (第二版) 光的波动性 光的干涉、衍射. 光波是横波 光的偏振 . 机械横波与纵波的区别 机 械 波 穿 过 狭 缝
14-9光的偏振性马吕斯定律 物理学教程 (第二版) 自然光偏振光 ◆自然光:一般光源发出的光中,包含着各个方向 的光矢量在所有可能的方向上的振幅都相等(轴对称) 这样的光叫自然光. 自然光以两互相垂直的互为独 立的(无确定的相位关系)振幅相 米 等的光振动表示,并各具有一半的 振动能量. 、二互相垂直方向是任选的. 符号表示 各光矢量间无固定的相位关系. 第十四章波动光学
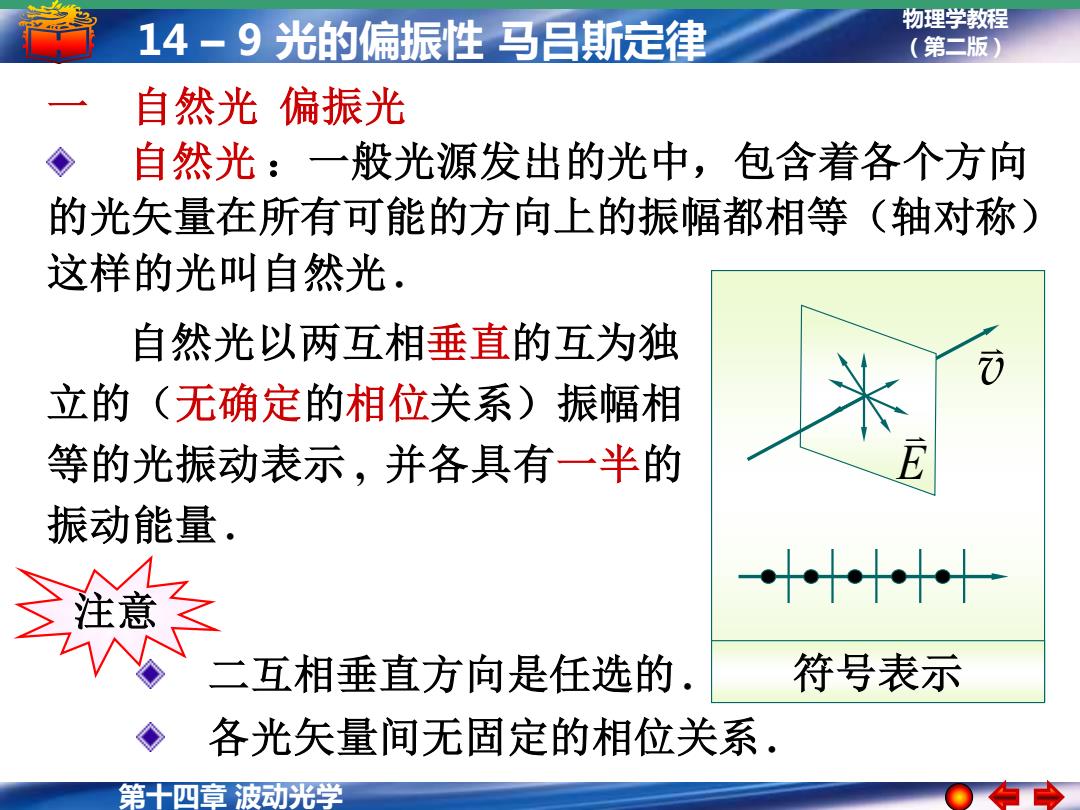
第十四章 波动光学 物理学教程 14 – 9 光的偏振性 马吕斯定律 (第二版) 一 自然光 偏振光 自然光 :一般光源发出的光中,包含着各个方向 的光矢量在所有可能的方向上的振幅都相等(轴对称) 这样的光叫自然光 . 自然光以两互相垂直的互为独 立的(无确定的相位关系)振幅相 等的光振动表示 , 并各具有一半的 振动能量 . 符号表示 v E 注意 各光矢量间无固定的相位关系 . 二互相垂直方向是任选的
14-9光的偏振性马吕斯定律 物理学教程 (第二版) 偏振光(线偏振光) 光振动只沿某一固定方向的光. 符号表示 十H 振动面 部分偏振光:某一方向的光振动比与之垂直方 向上的光振动占优势的光为部分偏振光. 符号表示 第十四章波动光学
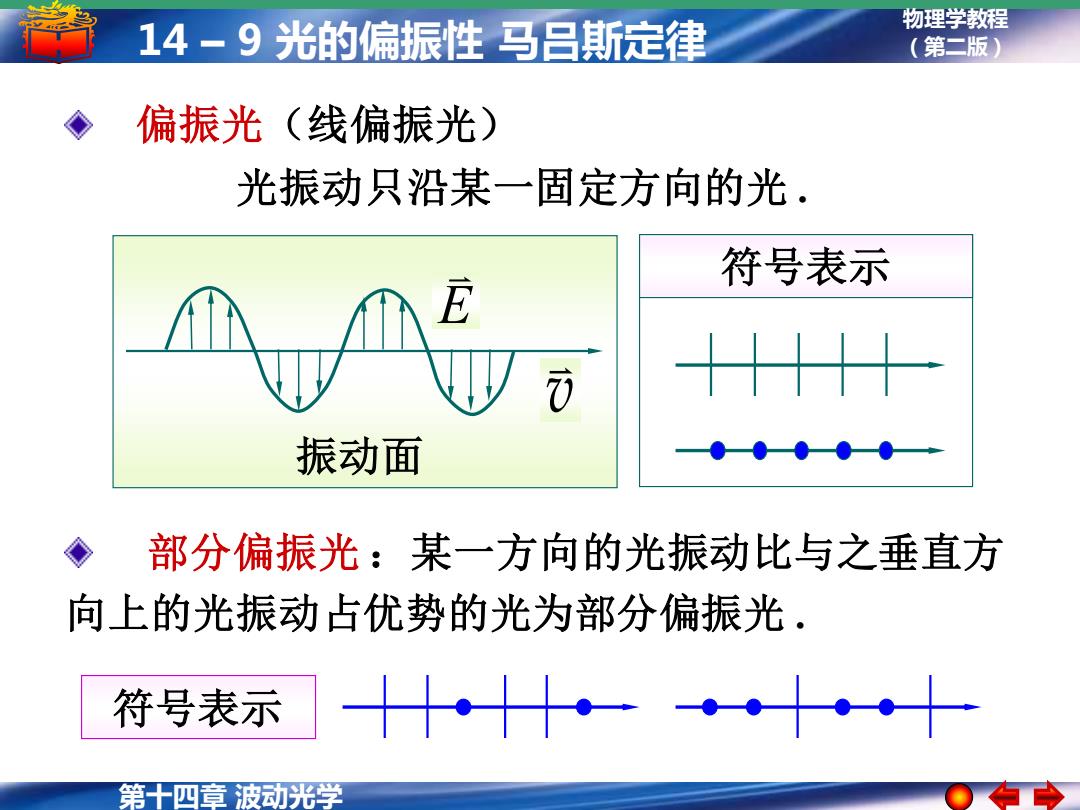
第十四章 波动光学 物理学教程 14 – 9 光的偏振性 马吕斯定律 (第二版) 偏振光(线偏振光) 符号表示 部分偏振光 :某一方向的光振动比与之垂直方 向上的光振动占优势的光为部分偏振光 . 符号表示 光振动只沿某一固定方向的光 . 振动面 v E

14-9光的偏振性马吕斯定律 物理学教程 (第二版) 二 偏振片起偏与检偏 ◆ 二向色性:某些物质能吸收某一方向的光振动, 而只让与这个方向垂直的光振动通过,这种性质称二 向色性 偏振片: 涂有二向色性材料的透明薄片. 偏振化方向:当自然光照射在偏振片上时,它 只让某一特定方向的光通过,这个方向叫此偏振片的 偏振化方向. 起 偏 起偏器 偏振化方向 第十四章波动光学
第十四章 波动光学 物理学教程 14 – 9 光的偏振性 马吕斯定律 (第二版) 起 偏 二 偏振片 起偏与检偏 二向色性 : 某些物质能吸收某一方向的光振动 , 而只让与这个方向垂直的光振动通过, 这种性质称二 向色性 . 偏振片 : 涂有二向色性材料的透明薄片 . 偏振化方向 : 当自然光照射在偏振片上时,它 只让某一特定方向的光通过,这个方向叫此偏振片的 偏振化方向 . 0 2 1 I 起偏器 偏振化方向 0 I
14-9光的偏振性马吕斯定律 物理学教程 (第二版) 检 十这 起偏器 检偏器 中 起偏器 检偏器 第十四章波动光学
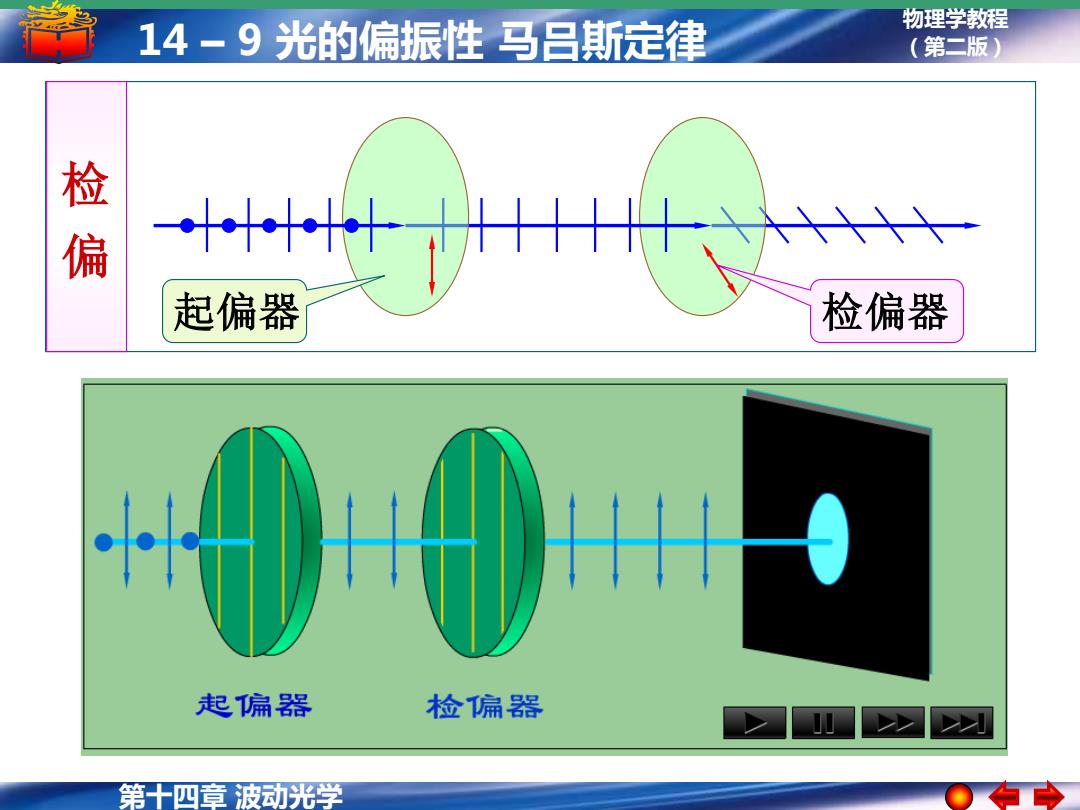
第十四章 波动光学 物理学教程 14 – 9 光的偏振性 马吕斯定律 (第二版) 检偏器 检 偏 起偏器
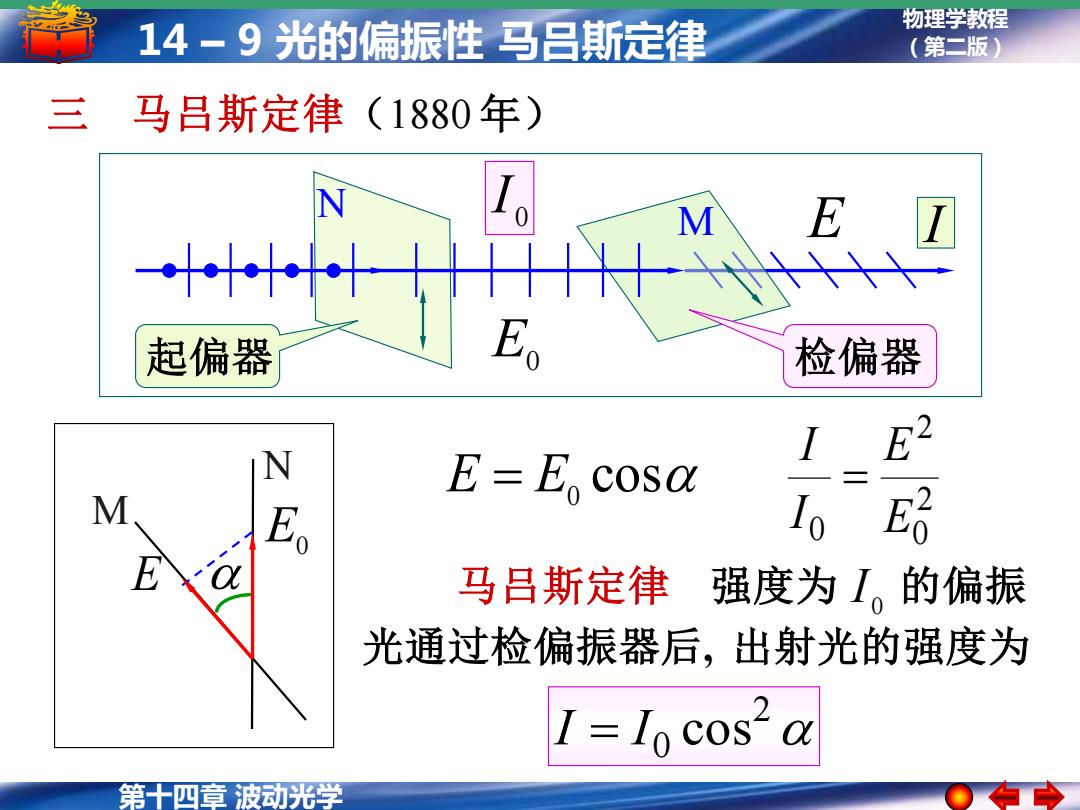
14-9光的偏振性马吕斯定律 物理学教程 (第二版) 三 马吕斯定律(1880年) N ME,☑ 起偏器 E 检偏器 N E=E cosa I E2 M E。 , 马吕斯定律 强度为I。的偏振 光通过检偏振器后,出射光的强度为 第十四章波动光学
第十四章 波动光学 物理学教程 14 – 9 光的偏振性 马吕斯定律 (第二版) N M 三 马吕斯定律(1880 年) E E0 E = E0 cos 2 0 2 0 E E I I = 起偏器 检偏器 0 I E I E0 N M 2 0 I = I cos 马吕斯定律 强度为 的偏振 光通过检偏振器后, 出射光的强度为 0 I

14-9光的偏振性马吕斯定律 物理学教程 (第二版) 例1有两个偏振片,一个用作起偏器,一个用作检 偏器.当它们偏振化方向间的夹角为30°时,一束单色 自然光穿过它们,出射光强为1;当它们偏振化方向间 的夹角为60°时,另一束单色自然光穿过它们,出射光 强为I2,且I1=I2·求两束单色自然光的强度之比. 解设两束单色自然光的强度分别为110和120· 经过起偏器后光强分别为 和 0 2 2 经过检偏器后 1=0c0230 20cos260 2 12 2 10=c0s230° 1 .1=12 120 c0s2609 第十四章波动光学
第十四章 波动光学 物理学教程 14 – 9 光的偏振性 马吕斯定律 (第二版) 例1 有两个偏振片,一个用作起偏器, 一个用作检 偏器. 当它们偏振化方向间的夹角为 时 , 一束单色 自然光穿过它们, 出射光强为 ; 当它们偏振化方向间 的夹角为 时, 另一束单色自然光穿过它们 , 出射光 强为 , 且 . 求两束单色自然光的强度之比 . 30 60 1 I 2 I 1 2 I = I 10 I 20 解 设两束单色自然光的强度分别为 和 I . 经过起偏器后光强分别为 和 . 2 20 I 2 10 I 经过检偏器后 cos 30 2 10 2 1 I I = cos 60 2 20 2 2 I I = 3 1 cos 6 0 cos 3 0 2 2 20 10 1 = 2 = = I I I I
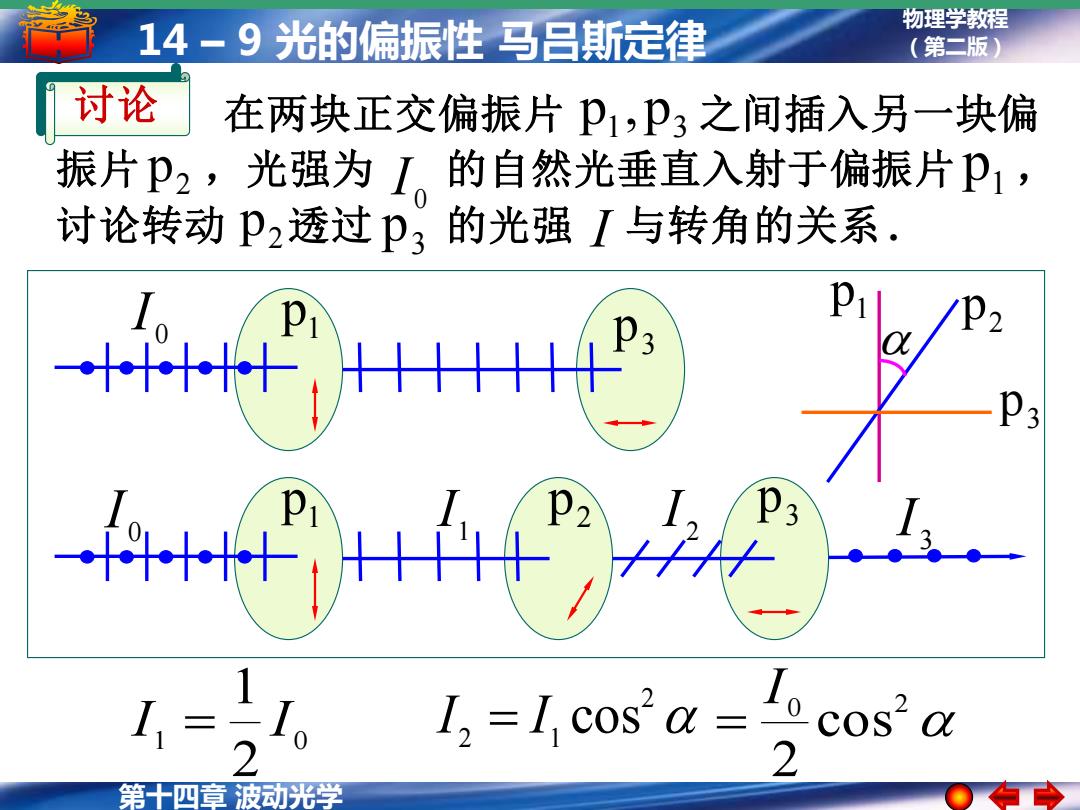
14-9光的偏振性马吕斯定律 物理学教程 (第二版) 讨论 在两块正交偏振片p,P3之间插入另一块偏 振片p2,光强为I。的自然光垂直入射于偏振片P1, 讨论转动p2透过p?的光强I与转角的关系. 1=1 cosa=to 第十四章波动光学
第十四章 波动光学 物理学教程 14 – 9 光的偏振性 马吕斯定律 (第二版) 2 2 1 I = I cos3 1 p p 0 I 0 I 1 I 3 p 2 p 1 p 2 I 3 I 2 p 3 p 1 p 1 0 2 1 I = I 0 2 cos 2 I = 在两块正交偏振片 之间插入另一块偏 振片 ,光强为 的自然光垂直入射于偏振片 , 讨论转动 透过 的光强 I 与转角的关系 . 1 p3 p , 2 p 2 p 3 p 0 I 1 p 讨论
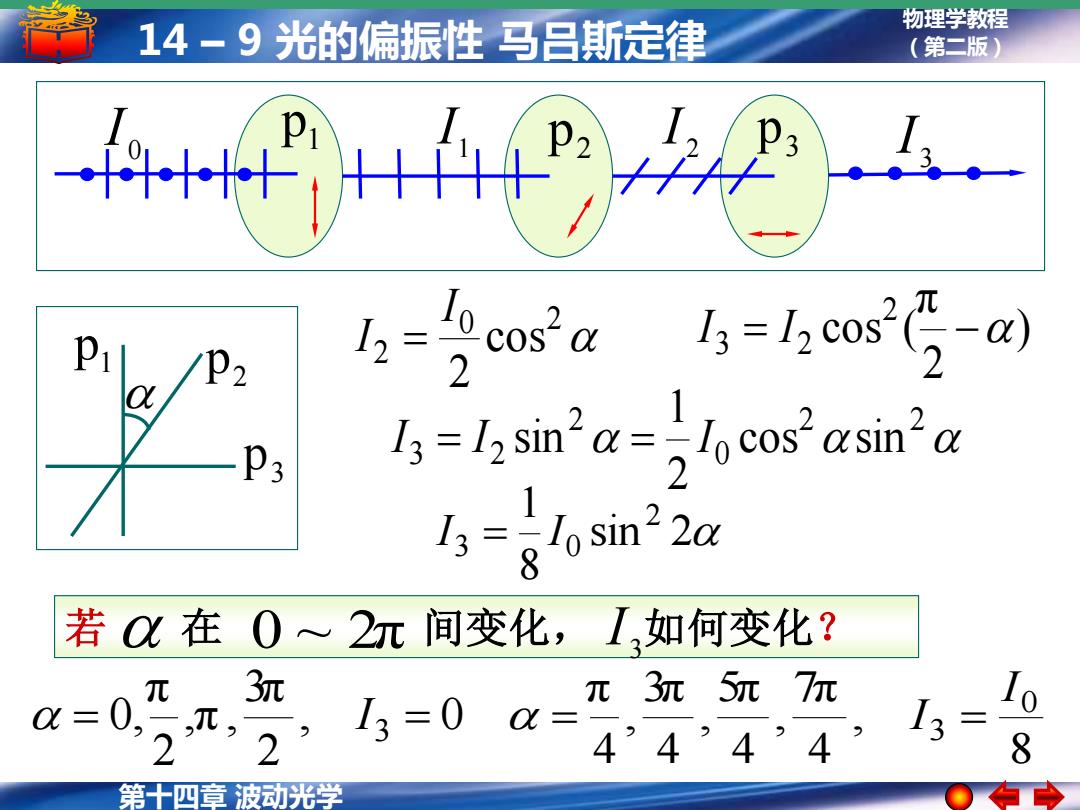
14-9光的偏振性马吕斯定律 物理学教程 (第二版) I2= 2 1 P: 13=12sin-a=lo cos2asin2a 3=。1osin22a 8 若0在0~2元间变化,I,如何变化? 元3元5元7元 0 0,2元2 0a= 4444,1= 8 第十四章波动光学
第十四章 波动光学 物理学教程 14 – 9 光的偏振性 马吕斯定律 (第二版) ) 2 π cos ( 2 0 2 I 3 = I 2 − 2 cos 2 I I = 2 2 0 2 3 2 cos sin 2 1 I = I sin = I sin 2 8 1 2 3 0 I = I 若 在 0 ~ 2π 间变化, I 3 如何变化? , 0 2 3π ,π , 2 π 0, = I 3 = 8 , 4 7π , 4 5π , 4 3π , 4 π 0 3 I = I = 0 I 1 I 3 p 2 p1 p 2 I 3 I 2 p 3 p 1 p