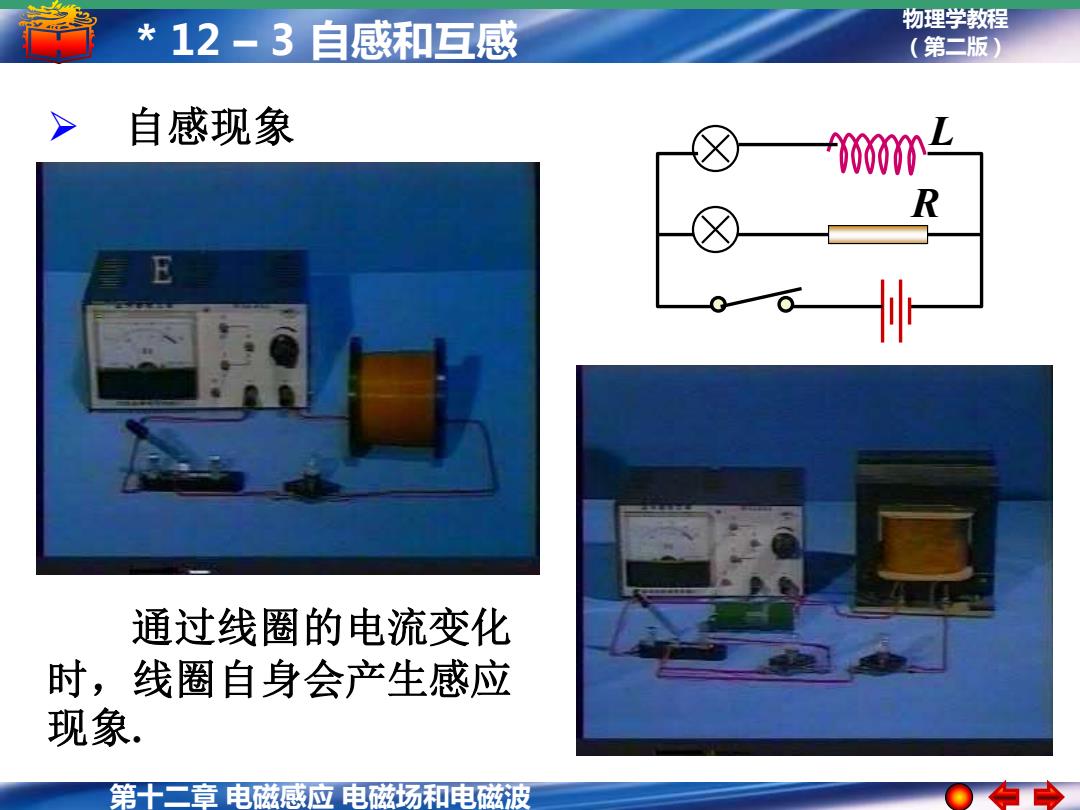
*12-3自感和互感 物理学教程 (第二版) 自感现象 Y00n- R 通过线圈的电流变化 时,线圈自身会产生感应 现象. 第十一章电滋感应电磁场和电磁波
第十二章 电磁感应 电磁场和电磁波 物理学教程 * 12 – 3 自感和互感 (第二版) ➢ 自感现象 R L 通过线圈的电流变化 时,线圈自身会产生感应 现象

*12-3自感和互感 物理学教程 (第二版) 自感电动势自感 穿过闭合电流回路的磁通量 Φ=LI 1)自感 L=I 若线圈有N匝, 杀 磁通匝数w=N更 自感L=wI 入 无铁磁质时,自感仅与线圈形状、磁介质及N有关. 第十二章电磁感应电磁场和电磁波
第十二章 电磁感应 电磁场和电磁波 物理学教程 * 12 – 3 自感和互感 (第二版) 一 自感电动势 自感 穿过闭合电流回路的磁通量 Φ = LI 1)自感 L =Φ I 若线圈有 N 匝, 磁通匝数 = NΦ 自感 L = I B I 无铁磁质时, 自感仅与线圈形状、磁介质及 N 有关. 注意

*12-3自感和互感 物理学教程 (第二版) dΦ =-(L d 2)自感电动势E=一 + dt dt dL 当 二0 dt 时, E=-L dt L=-E d 自感 dt 单位:1亨利(H)=1韦伯/安培 (1Wb/A) 1mH=10-3H,1μH=10-6H 第十二章电磁感应电磁场和电滋波
第十二章 电磁感应 电磁场和电磁波 物理学教程 * 12 – 3 自感和互感 (第二版) 0 d d = t L 当 时, t I L L d d E = − ) d d d d ( d d t L I t I L t Φ 2)自感电动势 EL = − = − + 自感 t I L L d d = −E 单位:1 亨利 ( H )= 1 韦伯 / 安培 (1 Wb / A) 1mH 10 H, 1μ H 10 H −3 −6 = =

*12-3自感和互感 物理学教程 (第二版) 3)自感的计算方法 例1 如图的长直密绕螺线管,已知I,S,W,u, 求其自感L.(忽略边缘效应) 解先设电流I→根据安培环路定理求得H→B →Φ→L, n-N/I B=uH unl w=NΦ=WBS N Nu IS 第十二章电磁感应电磁场和电磁波
第十二章 电磁感应 电磁场和电磁波 物理学教程 * 12 – 3 自感和互感 (第二版) 3)自感的计算方法 B = H = nI n = N l = NΦ= NBS IS l N = N L 例1 如图的长直密绕螺线管,已知 , 求其自感 . (忽略边缘效应) l, S,N, l S E 解 先设电流 I 根据安培环路定理求得 H B Φ L

*12-3自感和互感 物理学教程 (第二版) W W=NA IS N2 (一般情况可用下式 n=N/I V=IS 测量自感) l ..L=un2V E=-LY 4)自感的应用稳流,LC谐振电路,滤波电路, 感应圈等. 第十二章电磁感应电磁场和电磁波
第十二章 电磁感应 电磁场和电磁波 物理学教程 * 12 – 3 自感和互感 (第二版) t I L L d d E = − (一般情况可用下式 测量自感) l S E IS l N = N n = N l V = lS L n V 2 = S l N I L 2 = = 4)自感的应用 稳流 , LC 谐振电路, 滤波电路, 感应圈等

*12-3自感和互感 物理学教程 (第二版) 互感现象 在一个 线圈中通上 交流电,在 旁边的另一 线圈中会感 应电流,使 与之串连的 灯泡发光 第十二章电磁感应电磁场和电磁波
第十二章 电磁感应 电磁场和电磁波 物理学教程 * 12 – 3 自感和互感 (第二版) 互 感 现 象 在一个 线圈中通上 交流电,在 旁边的另一 线圈中会感 应电流, 使 与之串连的 灯泡发光

*12-3自感和互感 物理学教程 (第二版) 二 互感电动势互感 I,在I,电流回 B 路中所产生的磁通量 虫1=M2II I2在I1电流回路中所产生的磁通量虫2=M12I2 1)互感系数 (理论可证明) M12=M21=M= 1_2 I 表专双耳时个线的形状、大小、匝数相 对位置以及周围的磁介质有关(无铁磁质时为常 量). 第十一章电滋感应电磁场和电滋波
第十二章 电磁感应 电磁场和电磁波 物理学教程 * 12 – 3 自感和互感 (第二版) 二 互感电动势 互感 在 电流回 路中所产生的磁通量 1 I 2 I 21 21 1 Φ = M I I 2 在 I 1 电流回路 中所产生的磁通量 12 12 2 Φ = M I B1 B2 2 I 1 I 互感仅与两个线圈形状、大小、匝数、相 对位置以及周围的磁介质有关(无铁磁质时为常 量). 注意 1 )互感系数 (理论可证明) 2 1 2 1 2 1 1 2 2 1 I Φ I Φ M = M = M = =

*12-3自感和互感 物理学教程 (第二版) 2)互感电动势 E2=-M =-M dt E21 dt >互感系数 M E2 dl/dt dl,/dt 问:下列几种情况互感是否变化? 1)线框平行直导线移动; 2)线框垂直于直导线移动: 3)线框绕OC轴转动; 4)直导线中电流变化. 第十二章电磁感应电磁场和电磁波
第十二章 电磁感应 电磁场和电磁波 物理学教程 * 12 – 3 自感和互感 (第二版) I t I t M d d d 2 d 12 1 E21 E ➢ 互感系数 = − = − 问:下列几种情况互感是否变化? 1)线框平行直导线移动; 2)线框垂直于直导线移动; 3)线框绕 OC 轴转动; 4)直导线中电流变化. O C 2 )互感电动势 t I M d d 2 E12 = − t I M d d 1 E2 1 = −

*12-3自感和互感 物理学教程 (第二版) 例2两同轴长直密绕螺线管的互感 有两个长 度均为l,半径分别为r和r)(r1<r,),匝数分别为N和 N,的同轴长直密绕螺线管.求它们的互感M 解先设某一线圈中 通以电流I→求出另一 线圈的磁通量D→M 设半径为的线圈中 通有电流I,则 在P<片内 I=4o4 B1=61 第十二章电磁感应电磁场和电磁波
第十二章 电磁感应 电磁场和电磁波 物理学教程 * 12 – 3 自感和互感 (第二版) 例2 两同轴长直密绕螺线管的互感 有两个长 度均为l,半径分别为r1和r2( r1<r2 ),匝数分别为N1和 N2的同轴长直密绕螺线管.求它们的互感 M. 解 先设某一线圈中 通以电流 I 求出另一 线圈的磁通量 Φ M 设半径为 的线圈中 通有电流 , 则 1 r 1 I 1 0 1 1 1 1 0 I n I l N B = = 1 在 r r 内

*12-3自感和互感 物理学教程 (第二版) 1,=n B1=401 则穿过半径为严,的线圈 的磁通匝数为 w=N④1=N,Br2) =2lB1(π2) 代入B计算得=N21=4nn2I亿)I1 则 M12= on) I 第十二章电磁感应电磁场和电磁波
第十二章 电磁感应 电磁场和电磁波 物理学教程 * 12 – 3 自感和互感 (第二版) 1 0 1 1 1 1 0 I n I l N B = = (π ) 2 2 1 1 = n lB r 1 2 2 2 1 0 1 2 1 代入 计算得 = N Φ = n n l(π r )I B1 则 (π ) 2 0 1 2 1 1 2 2 1 1 2 n n l r I N Φ M = = 则穿过半径为 的线圈 的磁通匝数为 (π ) 2 2 21 2 1 1 = N Φ = N B r 2 r