高等教育出版社：《物理学教程》教材电子教案（PPT课件，马文蔚第二版）第十一章 恒定磁场 11-4 毕奥-萨伐尔定律

11-4毕奥-萨伐尔定律 物理学教程 (第二版) 毕奥一萨伐尔定律 dB (电流元在空间产生的磁场) dB= uo Idlsin 0 4π 2 dB dB= Ho Idx 4π 3 真空磁导率4，=4元×10-7N·A2 任意载流导线在点P处的磁感强度 磁感强度叠加原理 B-fdB-tl dtxr 4 第十一章恒定磁场

第十一章 恒定磁场 物理学教程 11 – 4 毕奥-萨伐尔定律 （第二版） I P * 一 毕奥—萨伐尔定律 (电流元在空间产生的磁场) 2 0 d sin 4π d r I l B   = 3 0 d 4π d r I l r B     =  真空磁导率 7 2 0 4π 10 N A − −  =   I l  d B  d 3 0 d 4π d r I l r B B      = =    任意载流导线在点 P 处的磁感强度 磁感强度叠加原理  r  I l  d r  B  d

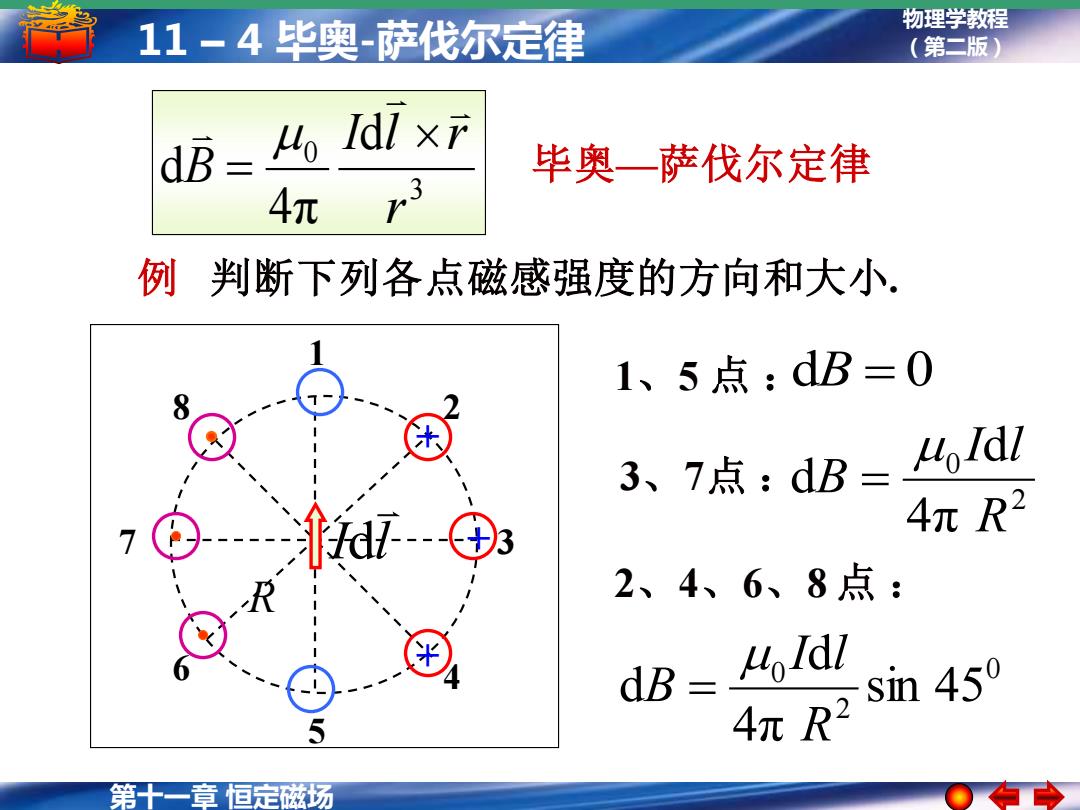
11-4毕奥-萨伐尔定律 物理学教程 (第二版) dB=4o Idlx 毕奥一萨伐尔定律 4π 3 例判断下列各点磁感强度的方向和大小 1、5点：dB=0 3、7点：dB= uoldl 4πR2 2、4、6、8点： dB=凸1dl 4πR2 n450 第十一章恒定磁场

第十一章 恒定磁场 物理学教程 11 – 4 毕奥-萨伐尔定律 （第二版） 1 2 3 4 5 6 7 8 I l  d 例 判断下列各点磁感强度的方向和大小. R + + + 1、5 点 ： dB = 0 3、7点 ： 2 0 4π d d R I l B  = 0 2 0 sin 45 4π d d R I l B  = 2、4、6、8 点 ： 3 0 d 4π d r I l r B     =  毕奥—萨伐尔定律

11-4毕奥-萨伐尔定律 物理学教程 (第二版) 二 毕奥-萨伐尔定律应用举例 dB方向均沿 例1载流长直导线的磁场. x轴的负方向 Idz sin 0 解 dB= 4 4元 2 Idz sin 0 dz B=∫dB= 4πcDr2 dB =-ro cote,r=r/sine dz=rde/sin20 B 18 sin ao 4π6 第十一章恒定磁场

第十一章 恒定磁场 物理学教程 11 – 4 毕奥-萨伐尔定律 （第二版） y x z I P C D o 0 r * 例1 载流长直导线的磁场. B  d 解 2 0 d sin 4π d r I z B   =   = = CD r I z B B 2 0 d sin 4π d   z = −r0 cot,r = r0 /sin   2 0 dz = r d /sin 方向均沿 x 轴的负方向 B  d 1 r  二 毕奥---萨伐尔定律应用举例  2   = 2 1 sin d 4π 0 0      r I B z dz

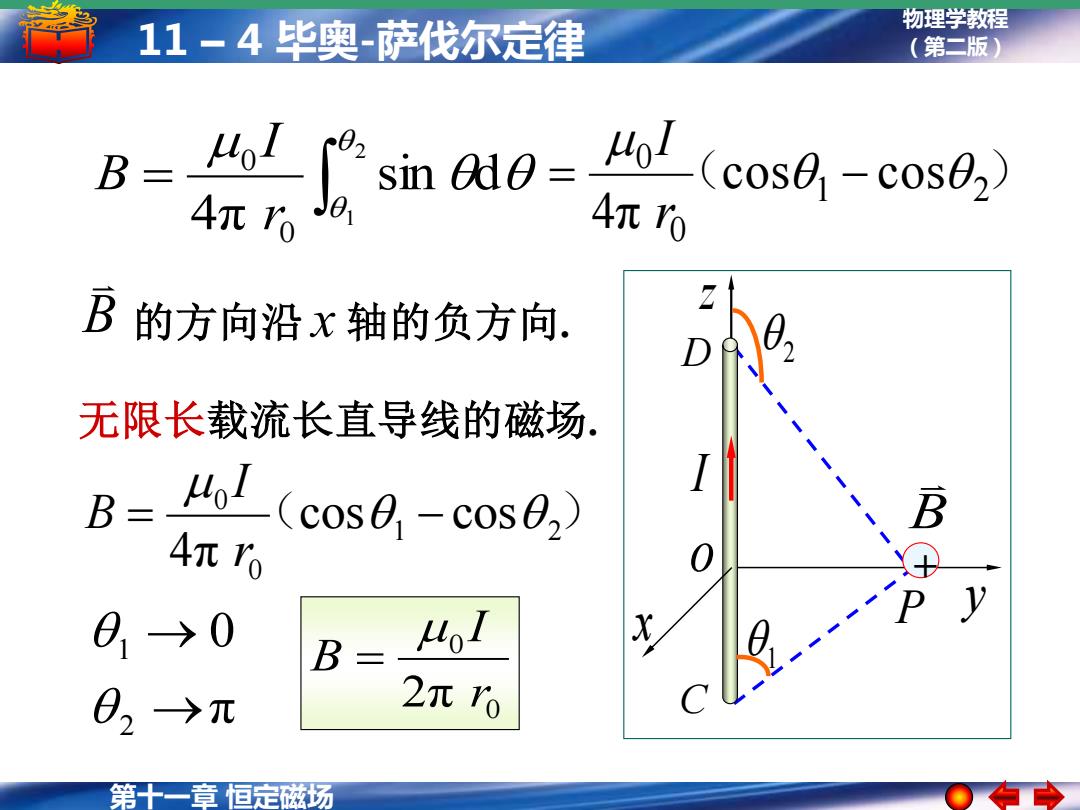
11-4毕奥-萨伐尔定律 物理学教程 (第二版) B 4 sin ae= 1(cos0-c0s6,) 4元ro 4元0 B 的方向沿x轴的负方向. 无限长载流长直导线的磁场. B= 41(cos0,-c0s02) 4元r0 B 40I 02→元 2L0 第十一章恒定磁场

第十一章 恒定磁场 物理学教程 11 – 4 毕奥-萨伐尔定律 （第二版） （ 1 2 ） 0 0 cos cos 4π    = − r I B 的方向沿 x 轴的负方向.   = 2 1 sin d 4π 0 0      r I B 无限长载流长直导线的磁场. π 0 2 1 → →   0 0 2π r I B  = （ 1 2 ） 0 0 cos cos 4π    = − r I B 1  2  P C D y x z o I B  +

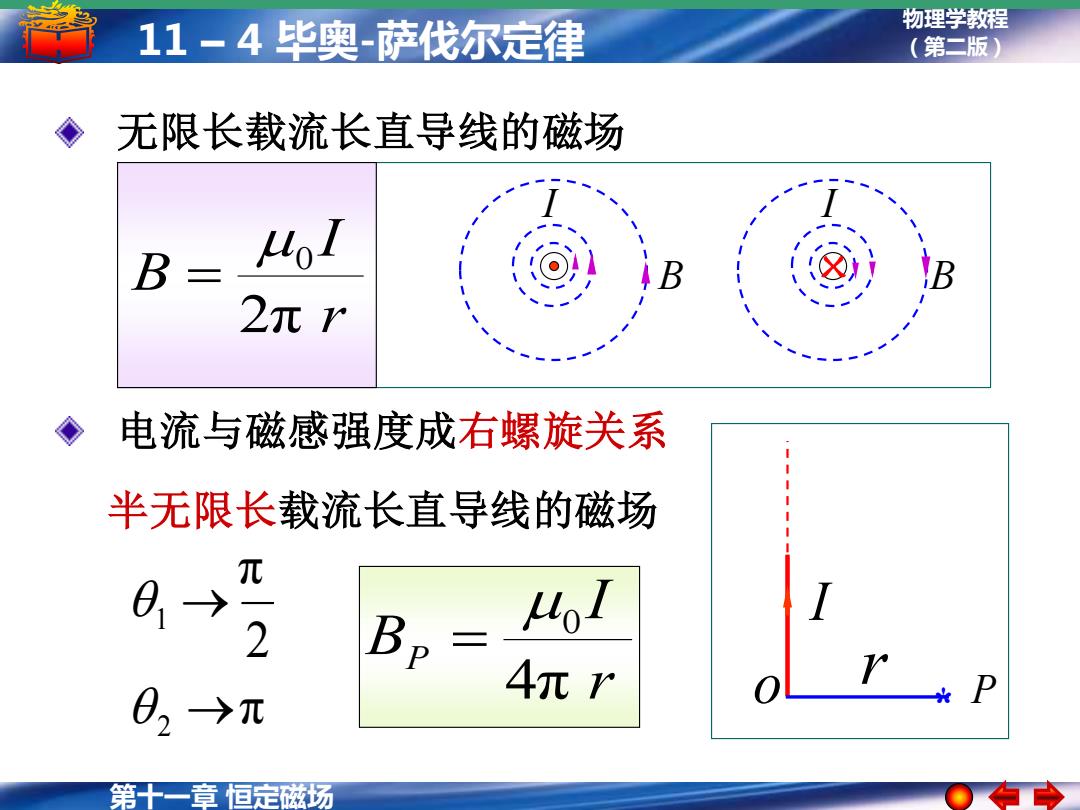
11-4毕奥-萨伐尔定律 物理学教程 (第二版) 无限长载流长直导线的磁场 B B 2πr 电流与磁感强度成右螺旋关系 半无限长载流长直导线的磁场 元 01 2 02→元 4元r 第十一章恒定磁场

第十一章 恒定磁场 物理学教程 11 – 4 毕奥-萨伐尔定律 （第二版） I B r I B 2π 0 = 电流与磁感强度成右螺旋关系 半无限长载流长直导线的磁场 r I BP 4π 0 = 无限长载流长直导线的磁场 r * P I o π 2 π 2 1 → →   I X B

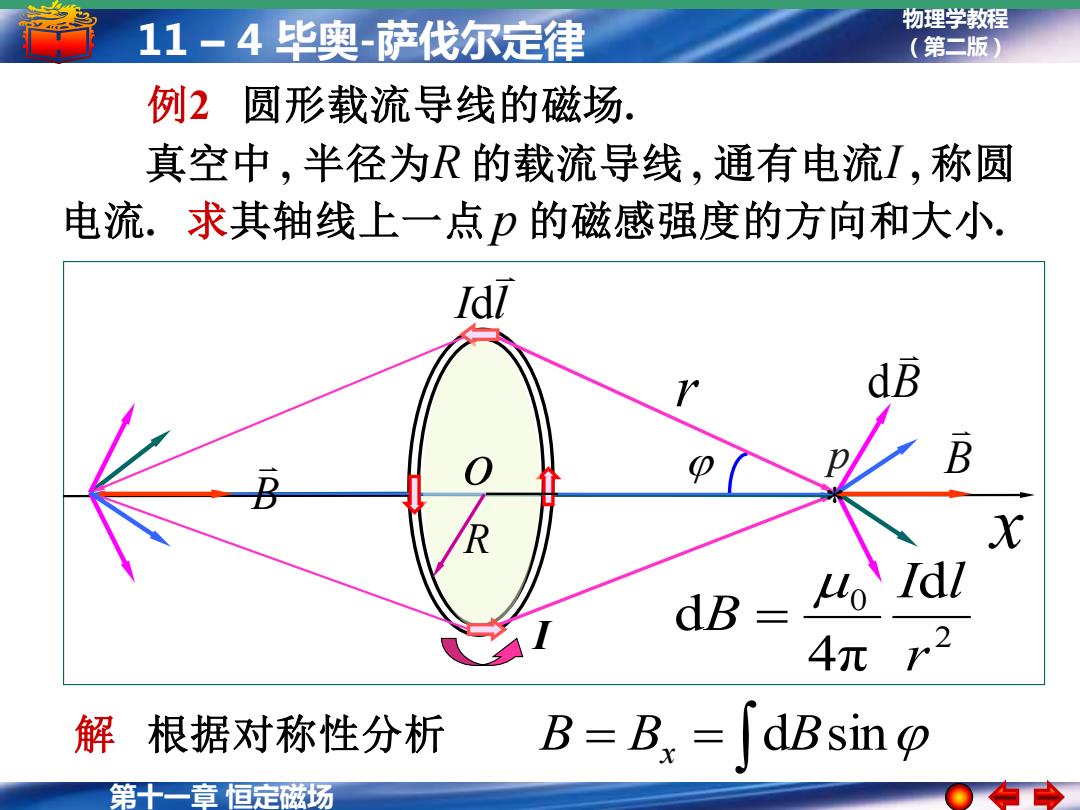
11-4毕奥-萨伐尔定律 物理学教程 (第二版) 例2圆形载流导线的磁场： 真空中，半径为R的载流导线，通有电流I,称圆 电流.求其轴线上一点p的磁感强度的方向和大小. Idl dB B X dB 4π 解根据对称性分析 B=Bx=「dBsin 第十一章恒定磁场

第十一章 恒定磁场 物理学教程 11 – 4 毕奥-萨伐尔定律 （第二版） I x 真空中 , 半径为R 的载流导线 , 通有电流I , 称圆 电流. 求其轴线上一点 p 的磁感强度的方向和大小. 解 根据对称性分析  B = Bx = dBsin 2 0 d 4π d r I l B  =  例2 圆形载流导线的磁场. r B  d B  B  I l  d p R o *

11-4毕奥-萨伐尔定律 物理学教程 (第二版) Idl cosa dB R r2=R2+x2 X B= 4元 Lo Idl B= MoIR dl dB 4πr3J0 4元 2 toIR2 I cos adl B=- dB, 4元 r2 2(x2+R2)为 第十一章恒定磁场

第十一章 恒定磁场 物理学教程 11 – 4 毕奥-萨伐尔定律 （第二版） x x R * p 2 0 cos d 4π d r I l Bx   =  = l r I l B 2 0 cos d 4π   2 2 2 cos r R x r R = +  =  = R l r IR B 2π 0 3 0 d 4π  2 3 2 2 2 0 （2 x R ） IR B + =  2 0 d 4π d r I l B  =    o B  d r I l  d

11-4毕奥-萨伐尔定律 物理学教程 (第二版) B= 4oIR2 2(x2+R2) N HoIR2 1)若线圈有W匝 B= 论 2(x2+R2)为 2)x>R B Lo IR2 B= MoIS 2x3 2πx3 第十一章恒定磁场

第十一章 恒定磁场 物理学教程 11 – 4 毕奥-萨伐尔定律 （第二版） 2 3 2 2 2 0 （2 x R ） IR B + =  R I B 2 0 3） x = 0 = 3 0 3 2 0 2 2π x IS B x IR B   4） x  R = ， = 2） x  0 B 的方向不变( 和 成右螺旋关系）  I B  1）若线圈有 N 匝 2 3 2 2 2 0 （2 x R ） N IR B + =  讨 论 x * B  o x I R

11-4毕奥-萨伐尔定律 物理学教程 (第二版) 三磁矩 m-ISe 例2中圆电流磁感强度 e. 公式也可写成 4oIR2 B Mom B 2x3 2πx3 B Lom 2元x /0 说明：只有当圆形电流的面积S很小，或场点距 圆电流很远时，才能把圆电流叫做磁偶极子. 第十一章恒定磁场

第十一章 恒定磁场 物理学教程 11 – 4 毕奥-萨伐尔定律 （第二版） I S 三 磁矩 en m IS   = m  n e  3 2 0 2x IR B  = m  I S n e  3 n 0 2π e x m B    = 3 0 2π x m B    = 说明：只有当圆形电流的面积 S 很小，或场点距 圆电流很远时，才能把圆电流叫做磁偶极子. 例2 中圆电流磁感强度 公式也可写成

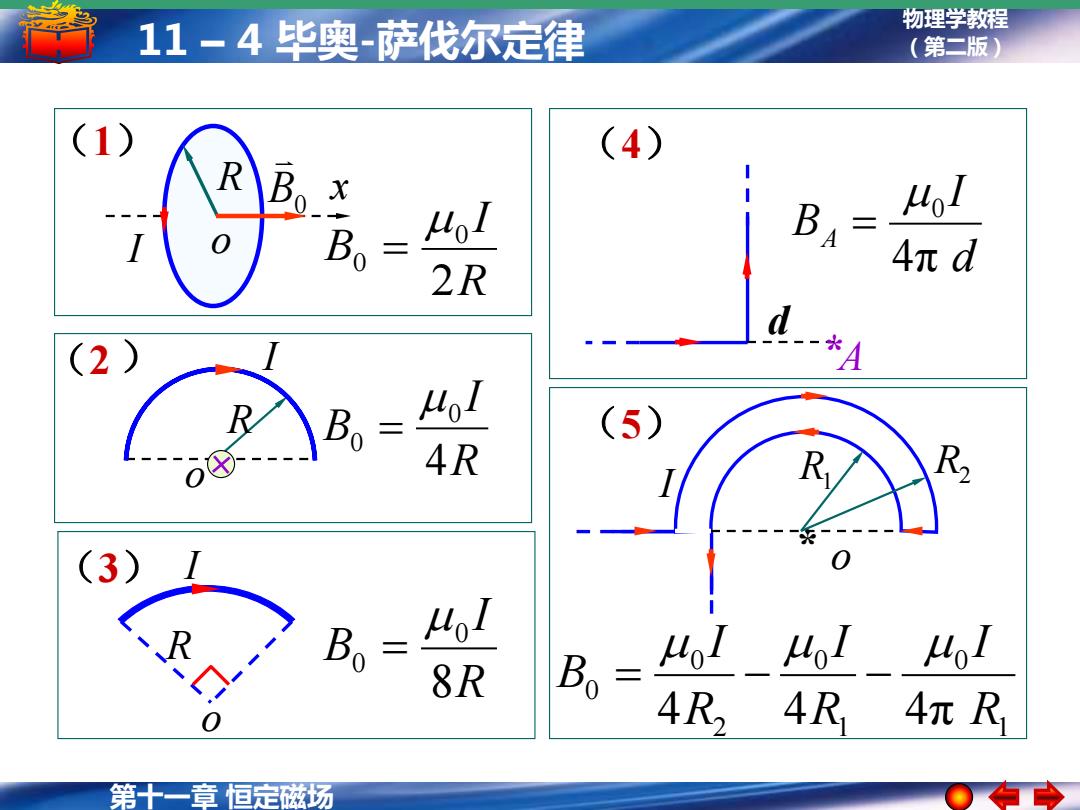
11-4毕奥-萨伐尔定律 物理学教程 (第二版) 1 (4) B 41 BA Hol 2R 4πd d A Bo= oI (5) 4R 3) 1 0 8R B。= MolMol ol 4R4R4πR 第十一章恒定磁场

第十一章 恒定磁场 物理学教程 11 – 4 毕奥-萨伐尔定律 （第二版） o I R1 R2 （5） * A d （4） * o （2 R ） I R （3） o I I R o （1） R I B 2 0 0  = R I B 4 0 0  = R I B 8 0 0  = 1 0 1 0 2 0 0 4 4 4π R I R I R I B    = − − d I BA 4π 0 = x B0 