10-5静电场的能量能量密度 物理学教程 (第二版) 电容器的电能 dw Udq 9 dg 2C C= dq W OU=-CU2 电容器贮存的电能 (任何形状电容器) W= 2C 第十章静电场中的导体与电介质
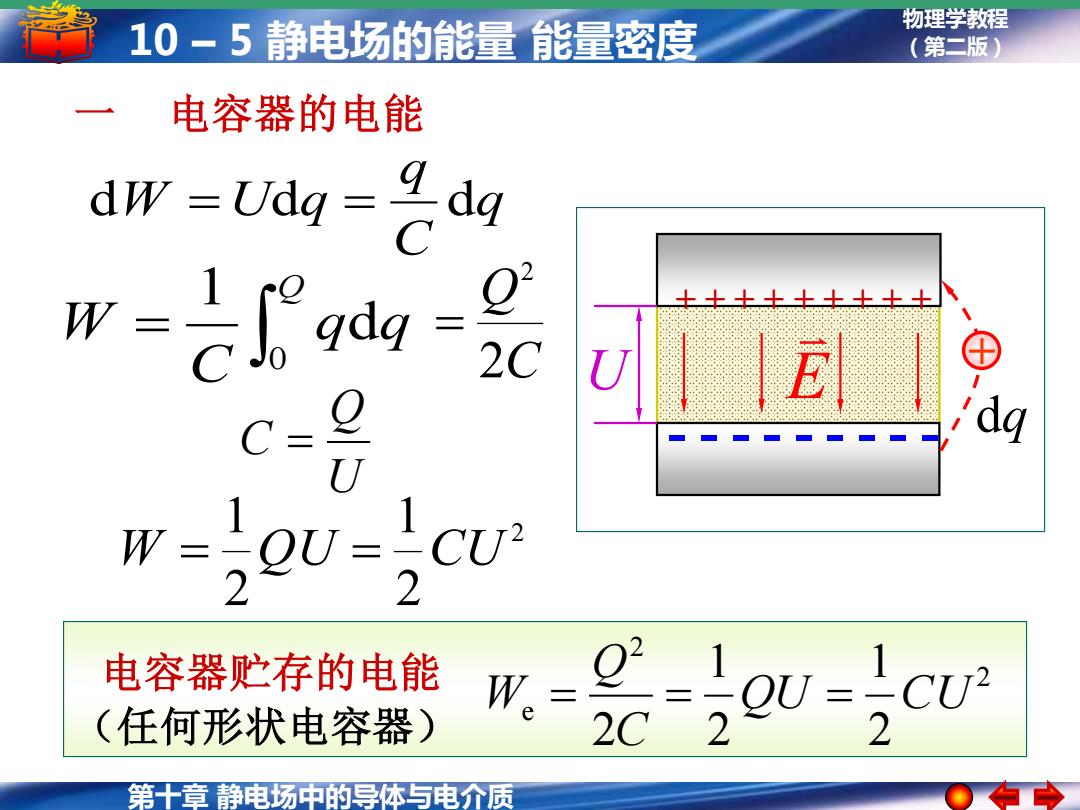
第十章 静电场中的导体与电介质 物理学教程 10 – 5 静电场的能量 能量密度 (第二版) + + + + + + + + + - - - - - - - - - E C Q 2 2 = 一 电容器的电能 q C q dW =Udq = d = Q q q C W 0 d 1 2 2 1 2 1 W = QU = CU U dq + U Q C = 2 2 e 2 1 2 1 2 QU CU C Q 电容器贮存的电能 W = = = (任何形状电容器)

10-5静电场的能量能量密度 物理学教程 (第二版) 二 静电场的能量 能量密度 CUd 1 2 电场能量密度W。= ED 2 2 物理意义 电场是一种物质,它具有能量 电场空间所存储的能量 e.-j小dr=2Eay 第十章静电场中的导体与电介质
第十章 静电场中的导体与电介质 物理学教程 10 – 5 静电场的能量 能量密度 (第二版) 二 静电场的能量 能量密度 2 e 2 1 W = CU 物理意义 电场是一种物质,它具有能量. 电场空间所存储的能量 = = V V W w V E dV 2 1 d 2 e e 电场能量密度 w E ED 2 1 2 1 2 e = = 2 ( ) 2 1 Ed d S = E Sd 2 2 1 =

10-5静电场的能量能量密度 物理学教程 (第二版) 例如图所示,球形电容器的内、外半径分别为R, 和R,,所带电荷为±Q·若在两球壳间充以电容率 为£的电介质,问此电容器贮存的电场能量为多少? 解 4πr2 1 =。E2= O 2 32π28r4 dWe wedy= 8π2d 所=∫d 8元EJR,2 8πεR R 第十章静电场中的导体与电介质
第十章 静电场中的导体与电介质 物理学教程 10 – 5 静电场的能量 能量密度 (第二版) R1 R2 例 如图所示, 球形电容器的内、外半径分别为 和 ,所带电荷为 .若在两球壳间充以电容率 为 的电介质,问此电容器贮存的电场能量为多少? R2 R1 Q 解 2 r 4π 1 e r Q E = r dr 2 4 2 2 e 2 32π 1 r Q w E = = r r Q W w V d 8π d d 2 2 e e = = ) 1 1 ( 8π d 8π d 1 2 2 R R 2 2 e e 2 1 R R Q r Q r W = W = = −

物理学教程 10一5静电场的能量能量密度 (第二版) Wo = 02 8元ER R22 4元8 RR R2-R 讨论 RR (1) W。= C=4兀8 2 c R-R (球形电容器电容) (2) R2-→0 W。= 8πR, (孤立导体球贮存的能量) 第十章静电场中的导体与电介质
第十章 静电场中的导体与电介质 物理学教程 10 – 5 静电场的能量 能量密度 (第二版) 2 1 2 1 2 1 2 2 e 4π 2 1 ) 1 1 ( 8 π R R R R Q R R Q W − = − = C Q W 2 2 e = 2 1 2 1 4π R R R R C − = (球形电容器电容) 讨 论 R2 → 1 2 e 8π R Q W = (1) (2) (孤立导体球贮存的能量)