
8一3理想气体的等体过程和等压过程摩尔热容 物理学教程 (第二版) 计算各等值过程的热量、功和内能的理论基础 pV= m (1) RT (理想气体的共性) M r do=dE+pdy 解决过程中能 (2) o-N+fnar 量转换的问题 (3)E=E(T) (理想气体的状态函数) (4) 各等值过程的特性. 第八章热力学基础
第八章 热力学基础 物理学教程 8 – 3 理想气体的等体过程和等压过程 摩尔热容 (第二版) 计算各等值过程的热量、功和内能的理论基础 RT M m (1) pV = (理想气体的共性) = + 2 1 d V V Q E p V dQ = dE + pdV (2) 解决过程中能 量转换的问题 (3) E = E(T) (理想气体的状态函数) (4) 各等值过程的特性
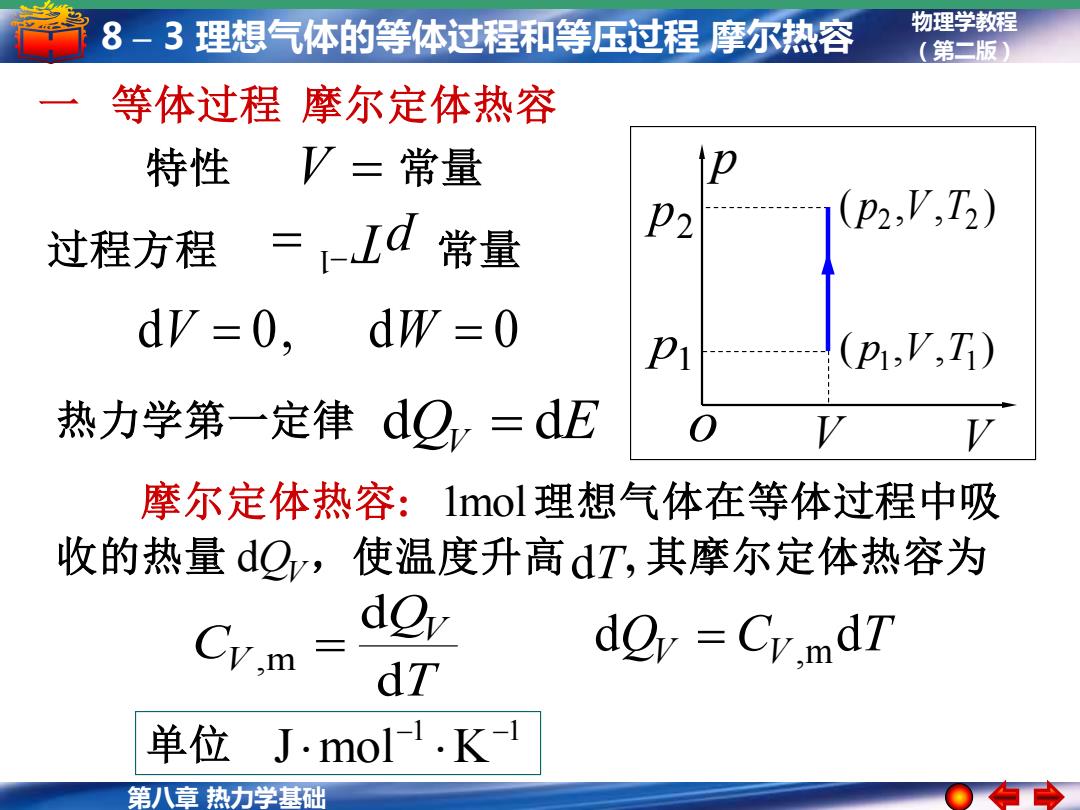
8-3理想气体的等体过程和等压过程摩尔热容 物理学教程 (第二版) 等体过程摩尔定体热容 特性 V=常量 p p2,V,T2) 过程方程 =-Ld常量 P2 dV=0, dw =0 (p1,V,T) 热力学第一定律dQ,=dE 摩尔定体热容:1mol理想气体在等体过程中吸 收的热量dQy,使温度升高dT,其摩尔定体热容为 d≌w V.m doy =Cy.mdT dT 单位J·mol1.K1 第八章热力学基础
第八章 热力学基础 物理学教程 8 – 3 理想气体的等体过程和等压过程 摩尔热容 (第二版) 单位 1 1 J mol K − − 一 等体过程 摩尔定体热容 dV = 0, dW = 0 过程方程 常量 = 1− pT 热力学第一定律 dQV = dE T Q C V V d d ,m = dQV = CV ,mdT 特性 V = 常量 ( , , ) p1 V T1 ( , , ) 2 V T2 p 2 p p1 V p o V 摩尔定体热容: 理想气体在等体过程中吸 收的热量 ,使温度升高 , 其摩尔定体热容为 1mol dQV dT

8一3理想气体的等体过程和等压过程摩尔热容 物理学教程 (第二版) d≌w doy =dE=CrdT=vCv.dT m Cr.m= dT M 热力学第一定律 ey=vCr.m(T2-T)=E2-E P2 (p2,V,T2) (p1,V,T) 等体升压 (p:V,Ti) 等体降压 (P2,V,T3) 第八章热力学基础
第八章 热力学基础 物理学教程 8 – 3 理想气体的等体过程和等压过程 摩尔热容 (第二版) C T C T M m QV E V d V d ' d = d = ,m = ,m ,m 2 1 2 1 热力学第一定律 QV =CV (T −T ) = E − E T Q C V V d d ,m = E1 QV E2 E1 QV E2 ( , , ) p1 V T1 ( , , ) 2 V T2 p p2 p1 V p o V 等 体 升 压 1 2 ( , , ) p1 V T1 ( , , ) 2 V T2 p p2 p1 V p o V 等 体 降 压 1 2

8-3理想气体的等体过程和等压过程摩尔热容 物理学教程 (第二版) 二 等压过程摩尔定压热容 特性卫=常量 (p,W,T)(p,,2) 过程方程 VT1=常量 功 W=p(V2-V) 热一律 dQ。=dE+dW V,V 摩尔定压热容:1mol理想气体在等压过程中吸 收的热量dQp,温度升高dT,其摩尔定压热容为 d№p dop Cp.mdT p,m dT 第八章热力学基础
第八章 热力学基础 物理学教程 8 – 3 理想气体的等体过程和等压过程 摩尔热容 (第二版) V2 ( , , ) V1 T1 p ( , , ) V2 T2 p p V1 p o V 1 2 二 等压过程 摩尔定压热容 过程方程 VT −1 = 常量 热一律 dQp = dE + dW T Q C p p d d ,m = 特 性 p = 常量 ( ) 功 W = p V2 −V1 摩尔定压热容: 理想气体在等压过程中吸 收的热量 ,温度升高 ,其摩尔定压热容为 1mol dQp dT dQp = Cp,mdT W

8-3理想气体的等体过程和等压过程摩尔热容 物理学教程 (第二版) dop Cp.mdT=dE+pdy dE =Cy.mdT pdy RdT 可得摩尔定压热容和摩尔定体热容的关系 Cp.m =Cym+R 摩尔热容比 y=Cpm/Cv.m W=p(V2-V)=vR(T2-T) p=vCp.m(T2-Ti),E2-E vCr.m (T2 -Ti) 箕八音热扇学其出
第八章 热力学基础 物理学教程 8 – 3 理想气体的等体过程和等压过程 摩尔热容 (第二版) dQp = Cp,mdT = dE + pdV pdV = RdT Cp,m = CV,m + R dE = CV ,mdT 可得摩尔定压热容和摩尔定体热容的关系 ( ) W = p V2 −V1 ( ) =R T2 −T1 ( ) E2 − E1 =CV ,m T2 −T1 ( ), Qp =Cp,m T2 −T1 摩尔热容比 = Cp,m CV,m
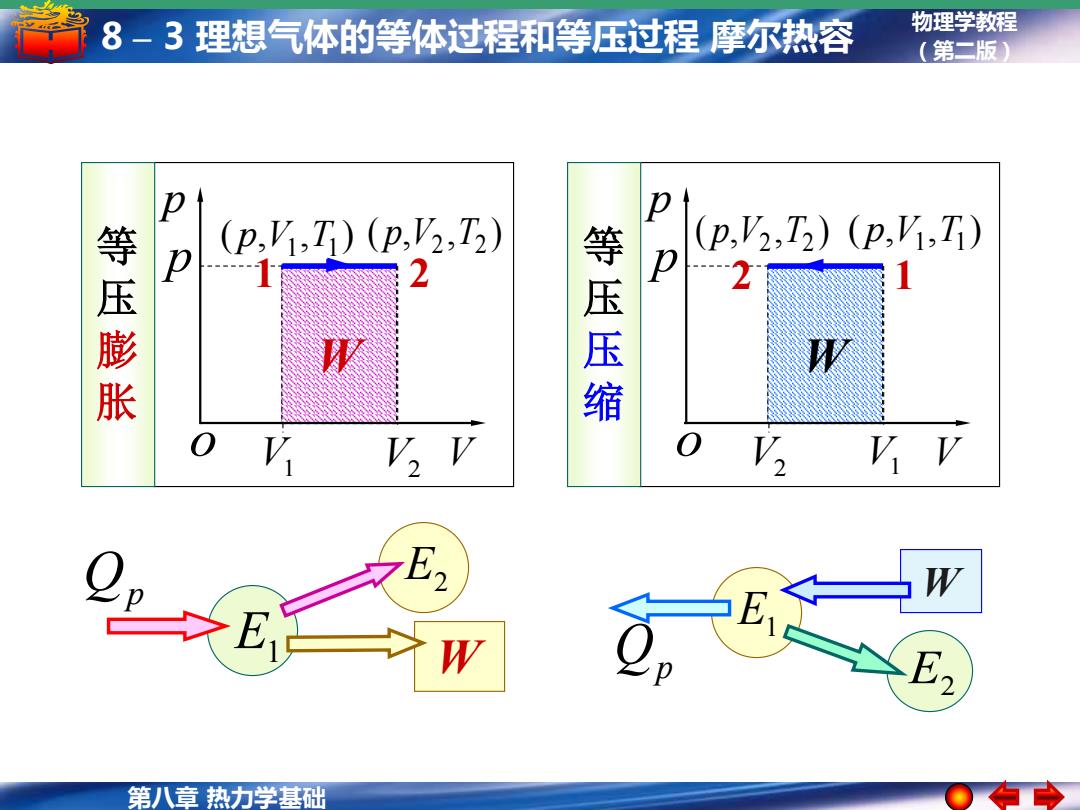
8-3理想气体的等体过程和等压过程摩尔热容 物理学教程 (第二版) (p,,Ti)(p,V2,T2) (p:V2:T2)(P,Vi,Ti) 等压膨胀 1 2 等压压缩 …2 0 V VV V,VV 第八章热力学基础
第八章 热力学基础 物理学教程 8 – 3 理想气体的等体过程和等压过程 摩尔热容 (第二版) V2 ( , , ) V1 T1 p ( , , ) V2 T2 p p V1 p o V 1 2 W 等 压 膨 胀 V2 ( , , ) V1 T1 ( , , ) p V2 T2 p p V1 p o V 2 1 W 等 压 压 缩 E1 E2 Qp E1 Qp E2 W W

8-3理想气体的等体过程和等压过程摩尔热容 物理学教程 (第二版) 理想气体摩尔热容理论计算 理想气体内能变化 dE=v- RdT 2 2 ,定体摩尔热容 Cvm R 2 ◆定压摩尔热容 Cp ● C 2 。摩尔热容比 p,m Y= 第八章热力学基础
第八章 热力学基础 物理学教程 8 – 3 理想气体的等体过程和等压过程 摩尔热容 (第二版) R T i E d 2 理想气体内能变化 d = R i CV 2 定体摩尔热容 ,m = R i Cp 2 2 ,m + 定压摩尔热容 = i i C C V p 2 ,m ,m + 摩尔热容比 = = 理想气体摩尔热容理论计算