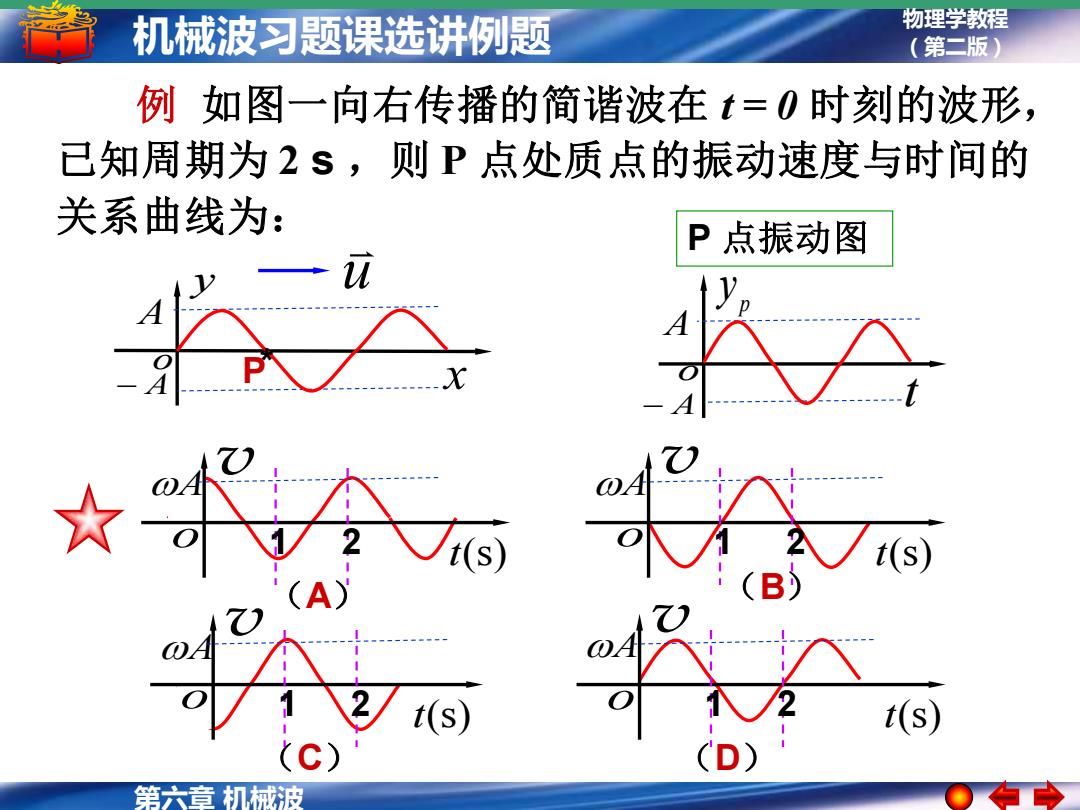
机械波习题课选讲例题 物理学教程 (第二版) 例如图一向右传播的简谐波在t=0时刻的波形, 已知周期为2s,则P点处质点的振动速度与时间的 关系曲线为: P点振动图 t(s) t(s) t(s)
物理学教程 (第二版) 第六章 机械波 机械波习题课选讲例题 v t(s) o A 1 2 (A) 例 如图一向右传播的简谐波在 t = 0 时刻的波形, 已知周期为 2 s ,则 P 点处质点的振动速度与时间的 关系曲线为: y − A x o A u P* p y − A t o A P 点振动图 t(s) o A 1 2 (C) v (B) t(s) o A 1 2 v t(s) o A 1 2 (D) v
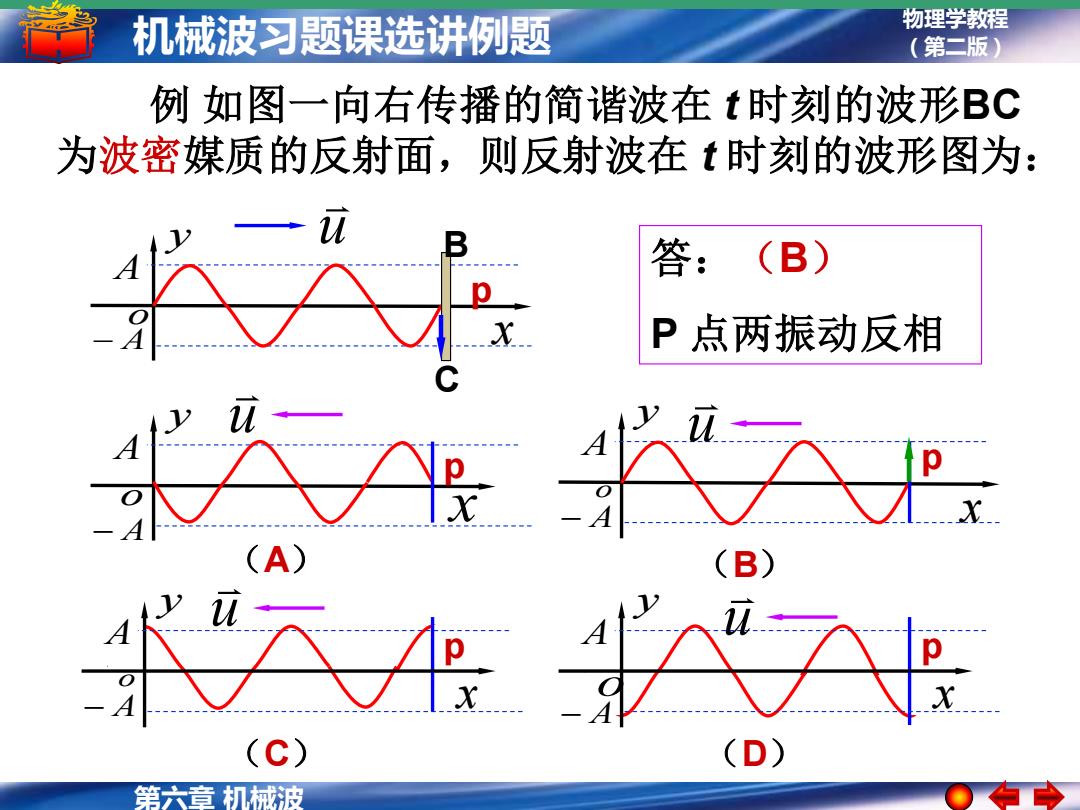
机械波习题课选讲例题 物理学教程 (第二版) 例如图一向右传播的简谐波在t时刻的波形BC 为波密媒质的反射面,则反射波在t时刻的波形图为: 答: (B) P点两振动反相 (C) (D) 第六章机械波
物理学教程 (第二版) 第六章 机械波 机械波习题课选讲例题 y − A x o A B C u p 例 如图一向右传播的简谐波在 t 时刻的波形BC 为波密媒质的反射面,则反射波在 t 时刻的波形图为: 答:(B) P 点两振动反相 y − A x o A y − A o A x u u (C) (D) y − A x o A u (A) p p p y − A x o A u (B) p

机械波习题课选讲例题 物理学教程 (第二版) 例 一平面简谐波动在弹性媒质中传播时,在 传播方向上媒质中某质元在负的最大位移处,则它的 能量是 (1)动能为零,势能最大★(2)动能为零,势能为零 (3)动能最大,势能最大 (4)动能最大,势能为零 例 在驻波中,两个相邻波节间各质点的振动 (1) 振幅相同,相位相同 大(2)振幅不同,相位相同 (3)振幅相同,相位不同 (4)振幅不同,相位不同 第六音机械波
物理学教程 (第二版) 第六章 机械波 机械波习题课选讲例题 例 一平面简谐波动在弹性媒质中传播时,在 传播方向上媒质中某质元在负的最大位移处,则它的 能量是 (1)动能为零,势能最大 (2)动能为零,势能为零 (3)动能最大,势能最大 (4)动能最大,势能为零 例 在驻波中,两个相邻波节间各质点的振动 (1)振幅相同,相位相同 (2)振幅不同,相位相同 (3)振幅相同,相位不同 (4)振幅不同,相位不同

机械波习题课选讲例题 物理学教程 (第二版) 例一平面机械波沿X轴负方向传播,已知x=-1m 处质点的振动方程为y=Acos(Ot+p),若波速为u 求此波的波函数. 解: 波函数 y=Acos[@(t+*)+o'] .'x=-1m y=Acos(ot+o) @li-)+p-o+p p=0+ u 2 y=Acoslo(t+*)++o] u u 第六章机械波
物理学教程 (第二版) 第六章 机械波 机械波习题课选讲例题 例 一平面机械波沿 轴负方向传播,已知 处质点的振动方程为 ,若波速为 求此波的波函数. x x = −1m y = Acos(t +) u x = −1m y = Acos(t +) − + =t + u t ) 1 ( u = + cos[ ( ) ] = + + + u u x y A t = cos[( + ) +] u x 解: 波函数 y A t

机械波习题课选讲例题 物理学教程 (第二版) 例一平面简谐波在t=0时刻的波形图如图, 设频率y=250Hz,且此时P点的运动方向向下, 求1)该波的波函数; 解:y=250H☑ y(m) 元=200m :0p<0 !x(m) 00m ∴.波向X轴负向传播 y=Ac0s[2π(250t+ x)+p] 2 24 兀 V2A/2 .t=0,x=0y= 0<0 .0= 4 第六音机械波
物理学教程 (第二版) 第六章 机械波 机械波习题课选讲例题 2A 2 100m y(m) − A x(m) o A P = 200m ) ] 200 = cos[ π(250 + + x y A 2 t 例 一平面简谐波在 时刻的波形图如图, 设频率 ,且此时 P 点的运动方向向下, 求 1)该波的波函数; = 250Hz t = 0 0 p v 0 2 2 = 0, = 0 = v A t x y 4 π = 解: 波向 x 轴负向传播 = 250Hz y A O 2A 2
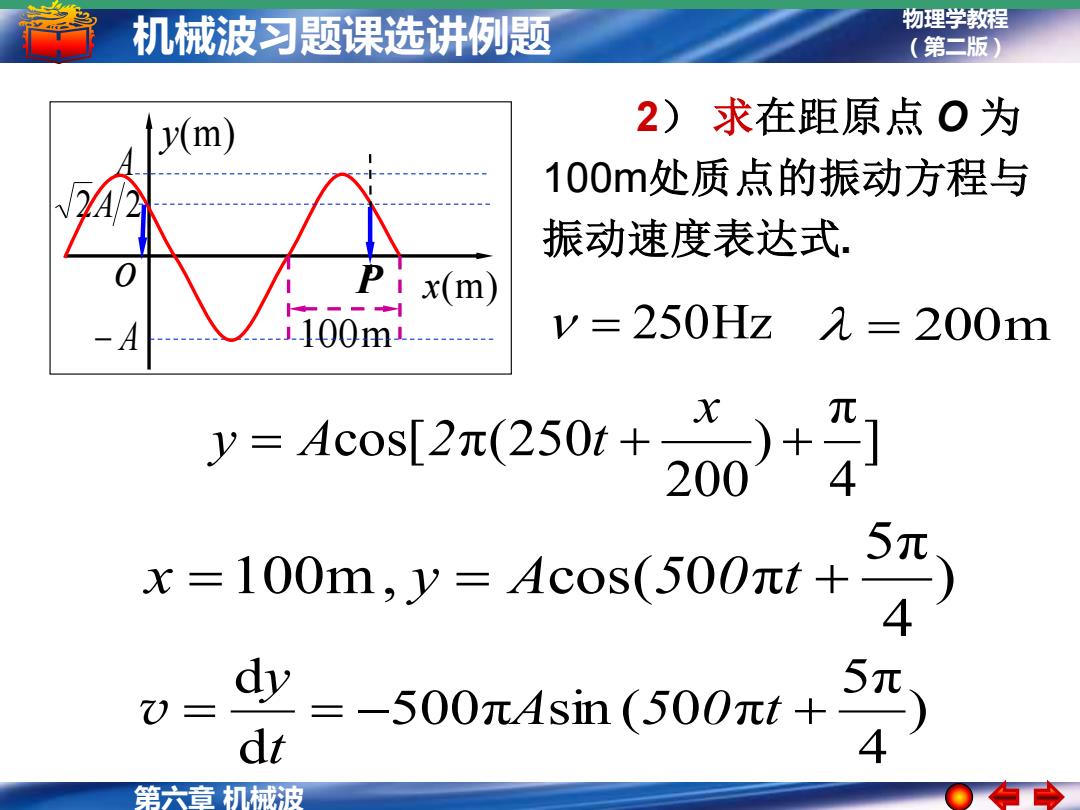
机械波习题课选讲例题 物理学教程 (第二版) (m) 2)求在距原点O为 100m处质点的振动方程与 振动速度表达式 Ix(m 1100m y=250Hz元=200m y=4eow2x(250+20)+孕 5元 x=100m,y=Acos(500nt+ dv =-500元Asin(500πt+ 5元 dt 第六章机械波
物理学教程 (第二版) 第六章 机械波 机械波习题课选讲例题 ] 4 π ) 200 = cos[ π(250 + + x y A 2 t ) 4 5π x =100m, y = Acos(500πt + ) 4 5π 500π sin ( 0 π d d = = − A 5 0 t + t y v 2) 求在距原点 O 为 100m处质点的振动方程与 振动速度表达式. = 250Hz = 200m 2A 2 100m y(m) − A x(m) o A P

机械波习题课选讲例题 物理学教程 (第二版) 例一简谐波沿Ox轴正向传播,已知振幅、频率 和速度分别为A,y,u,设t=t'时的波形曲线如 图,求1)X=0处质点振动方程;2)该波的波函数. t =t' 解:y。=AC0s(2πt+p) t=t,x=0y=00<0 2πvt+0=2 元 2πVt' yo=Acos[2πv(t-t)+ 2 波函数 y=Acos2πt-1'-衫+g 第六音机械波
物理学教程 (第二版) 第六章 机械波 机械波习题课选讲例题 u y t = t − A x o A y = Acos(2πt +) o 例 一简谐波沿 轴正向传播,已知振幅、频率 和速度分别为 ,设 时的波形曲线如 图,求 1) 处质点振动方程;2)该波的波函数. ox A, ,u t = t x = 0 = − 2πt 2 π 2 π 2π t + = t = t , x = 0 y = 0 v 0 ] 2 π yo = Acos[2π (t −t) + ] 2 π = cos[2π ( − − ) + u x 波函数 y A t t v 解:

机械波习题课选讲例题 物理学教程 (第二版) 例一简谐波沿0x轴正向传播,人=4m,T=4s 已知x=0点振动曲线如图,求1)x=0点振动方 程、2)波函数。 √2 y102m) =v2×102co2r4+0m N2/2 tS) t=0,x=0y=A/2v<0 波函数 y=V2×102cos24-+1m 第六章机械波
物理学教程 (第二版) 第六章 机械波 机械波习题课选讲例题 例 一简谐波沿 轴正向传播, 已知 点振动曲线如图,求 1) 点振动方 程、2)波函数。 ox = 4m,T = 4s x = 0 x = 0 2 (10 m) −2 y 2 2 − 2 t(s) o )m 4 2 10 cos(2π 2 = + − t yo ]m 3 π ) 4 4 2 10 cos[2π( 2 = − + − t x 波函数 y t = 0, x = 0 y = A 2 v 0 y o A 3 π = A 2
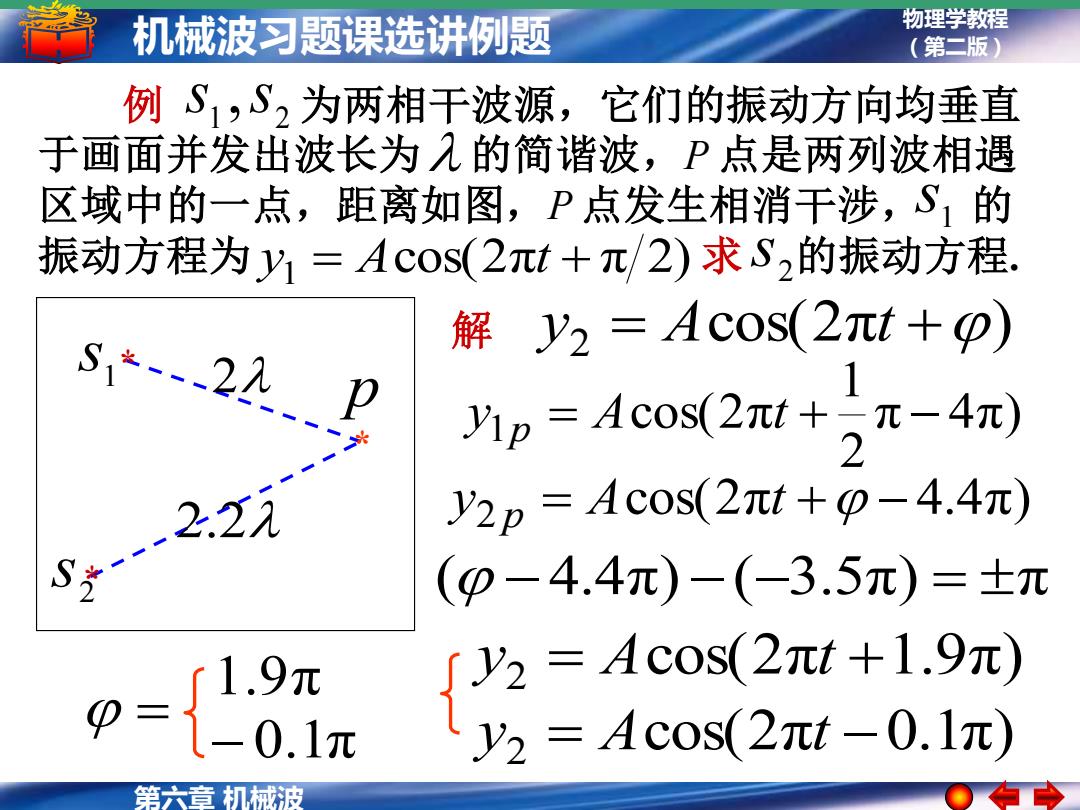
机械波习题课选讲例题 物理学教程 (第二版) 例S1,S,为两相干波源,它们的振动方向均垂直 于画面并发出波长为入的简谐波,P点是两列波相遇 区域中的一点,距离如图,P点发生相消干涉,S,的 振动方程为y1=Ac0$(2πt+π/2)求S2的振动方程, 解y2=Ac0s(2πt+p) 1 yM1p=Ac0s(2πt+π-4元) 2 -2.21 y2p=Ac0s(2πt+p-4.4元) S (p-4.4π)-(-3.5π)=±元 %=Acos(2t+1.9元) y2=Ac0$(2πt-0.1π) 第六音机械波
物理学教程 (第二版) 第六章 机械波 机械波习题课选讲例题 例 为两相干波源,它们的振动方向均垂直 于画面并发出波长为 的简谐波,P 点是两列波相遇 区域中的一点,距离如图,P 点发生相消干涉, 的 振动方程为 求 的振动方程. 1 2 s ,s 1 s 2 s cos(2π π 2) y1 = A t + * * 2 2.2 1 s 2 s p * cos(2π ) y2 = A t + π 4π) 2 1 y1p = Acos(2πt + − cos(2π 4.4π) y2 p = A t + − ( − 4.4π) −(−3.5π) = π cos(2π 0.1π) y2 = A t − cos(2π 1.9π) y2 = A t + = 1.9π − 0.1π 解

机械波习题课选讲例题 物理学教程 (第二版) 例:干涉消声器结构原理图,当发电机噪声经过 排气管达到A时分成两路在B点相遇,声波干涉相 消,若频率y=300Hz,则弯管与直管的长度差至 少应为多少?(声波的速度u=340m/s) △p=2π(12-1)/九=2元△r/2 干涉相消时△0=(2k+1)π k=0,±1,+2,. △r=(2k+1)元/2 k=0(△r)mm =0.57m 2 2v 实际应用时,常将不同频率的消声器串接在一起。 第六章机械波
物理学教程 (第二版) 第六章 机械波 机械波习题课选讲例题 A B 1 r 2 = 2π(r2 − r1 ) = 2πr r r = (2k +1) 2 0.5 7m 2 2 0 ( ) = min = = = u k r 例:干涉消声器结构原理图,当发电机噪声经过 排气管达到 A 时分成两路在 B 点相遇,声波干涉相 消,若频率 ,则弯管与直管的长度差至 少应为多少?(声波的速度 ) = 300Hz u = 340m/s 实际应用时,常将不同频率的消声器串接在一起。 干涉相消时 = (2k +1)π k = 0,1,2,