
物理学教程 4-2力矩转动定律转动惯量 (第二版) 问:在质点问题中,我们将物体所受的力均作 用于同一点,并仅考虑力的大小和方向所产生的作 用;在刚体问题中,我们是否也可以如此处理?力 的作用点的位置对物体的运动有影响吗? ∑F=0,∑M,=0 圆盘静止不动 ∑E=0,∑M,≠0 圆盘绕圆心转动 力矩可以反映力的作用点的位置对物体运动的影响, 第四章刚体转动
第四章 刚体转动 物理学教程 4 – 2 力矩 转动定律 转动惯量 (第二版) 问:在质点问题中,我们将物体所受的力均作 用于同一点,并仅考虑力的大小和方向所产生的作 用;在刚体问题中,我们是否也可以如此处理?力 的作用点的位置对物体的运动有影响吗? Fi = 0 , Mi = 0 圆盘静止不动 Fi = 0 , Mi 0 圆盘绕圆心转动 F F − F F − 力矩可以反映力的作用点的位置对物体运动的影响

物理学教程 4-2力矩转动定律转动惯量 (第二版) 力矩 刚体绕Oz轴旋转,力云作用在刚体上点P, 且在转动平面内,户为由点O到力的作用点P的径 矢. F对转轴Z的力矩 M=产×F M-Frsin 0=Fd d:力臂 第四章刚体转动
第四章 刚体转动 物理学教程 4 – 2 力矩 转动定律 转动惯量 (第二版) P z * M = Frsin = Fd O M F r d d : 力臂 刚体绕 O z 轴旋转 , 力 作用在刚体上点P , 且在转动平面内, 为由点O 到力的作用点 P 的径 矢 . F r M r F = F 对转轴 Z 的力矩 一 力矩 M
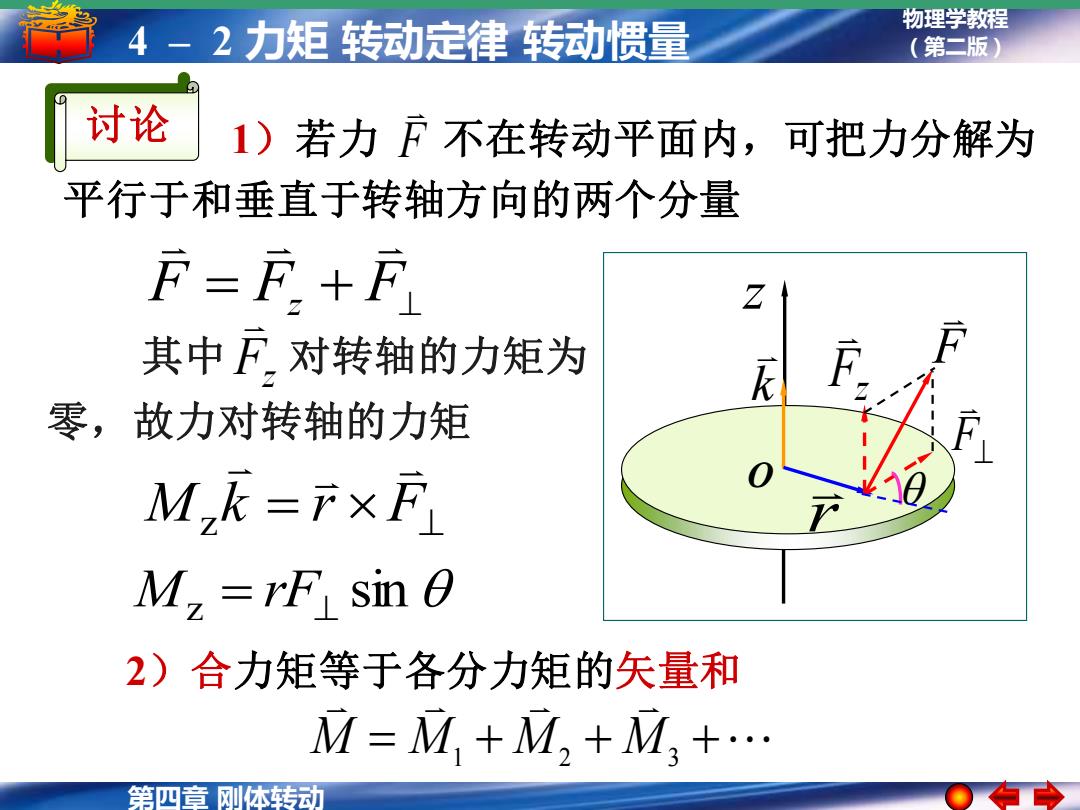
物理学教程 4-2力矩转动定律转动惯量 (第二版) 讨论 1)若力F不在转动平面内,可把力分解为 平行于和垂直于转轴方向的两个分量 F=F+F 其中F对转轴的力矩为 零,故力对转轴的力矩 M2E=产×F M,=rF sin 0 2)合力矩等于各分力矩的矢量和 M=M,+M,+M,+… 第四章刚体转动
第四章 刚体转动 物理学教程 4 – 2 力矩 转动定律 转动惯量 (第二版) z O k F r 讨论 F = F z + F⊥ = F⊥ M k r z Mz = rF⊥ sin Fz F⊥ 1)若力 不在转动平面内,可把力分解为 平行于和垂直于转轴方向的两个分量 F 2)合力矩等于各分力矩的矢量和 M = M1 + M2 + M3 + 其中 对转轴的力矩为 零,故力对转轴的力矩 Fz
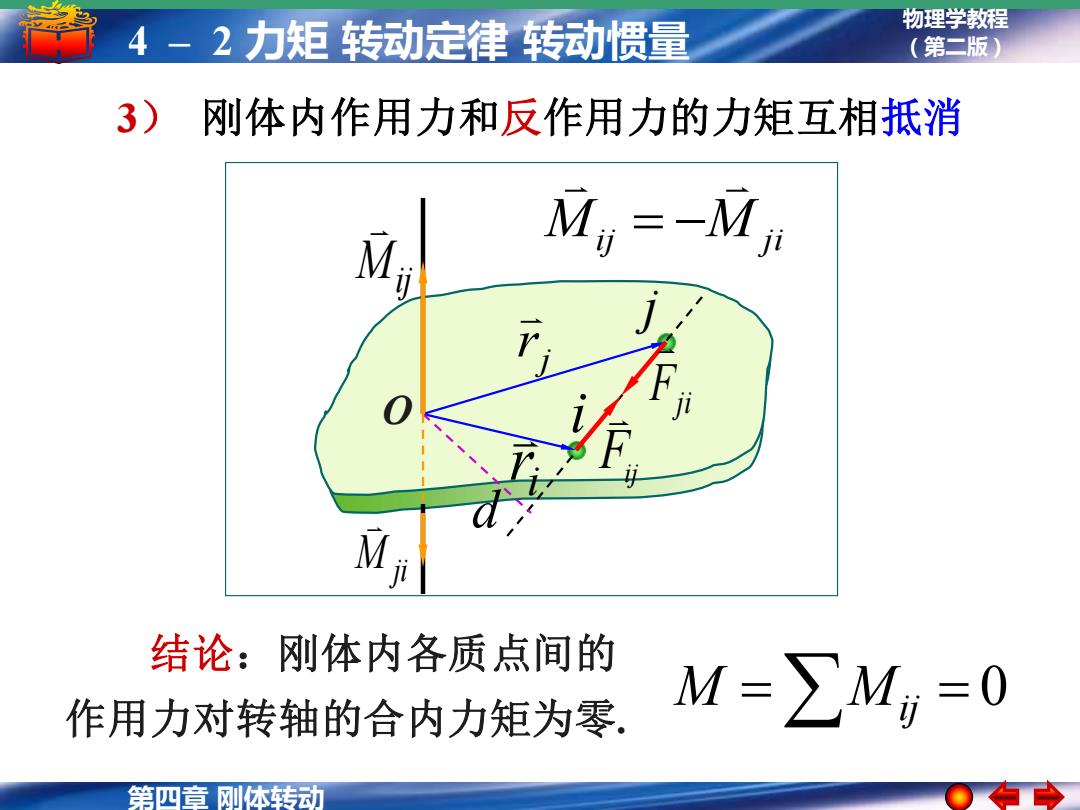
4-2力矩转动定律转动惯量 物理学教程 (第二版) 3)刚体内作用力和反作用力的力矩互相抵消 M My=-Mn M 结论:刚体内各质点间的 作用力对转轴的合内力矩为零. M=∑M,=0 第四章刚体转动
第四章 刚体转动 物理学教程 4 – 2 力矩 转动定律 转动惯量 (第二版) 3) 刚体内作用力和反作用力的力矩互相抵消 Mij M ji = − j r i r i j Fij Fji d O Mij M ji 结论:刚体内各质点间的 作用力对转轴的合内力矩为零. = = 0 M Mij

物理学教程 4-2力矩转动定律转动惯量 (第二版) 二 转动定律 Ft=(△m;)a=mro M;=rFt=(△m;)a △m '.'at =ra ∴.M,=(△m;)ra M=∑M,=∑(△m,2a&=a∑(Am;): 转动惯量 J=∑△m, 转动定律 M=Ja 第四章刚体转动
第四章 刚体转动 物理学教程 4 – 2 力矩 转动定律 转动惯量 (第二版) z 二 转动定律 Fit = (mi )at = mr 2 ( ) i i i M = m r i i i i i M r F m a r t t = = ( ) mi i r O Fit at = r 2 2 ( ) ( ) i i i i i M = M = m r = m r 转动定律 M = J 2 i i ➢ 转动惯量 J =m r

4-2力矩转动定律转动惯量 物理学教程 (第二版) 转动定律 M=Ja J=∑Am, 刚体定轴转动的角加速度与它所受的合外力矩成正 比,与刚体的转动惯量成反比. 转动惯量物理意义:转动惯性的量度, 质量连续分布刚体的转动惯量 J=∑Am2=∫r2dm 质量元:dm 三法海条转动惯量的大小取决于刚你的窑度、儿何 形状及转轴的位置. 第四章刚体转动
第四章 刚体转动 物理学教程 4 – 2 力矩 转动定律 转动惯量 (第二版) ➢ 转动惯量物理意义:转动惯性的量度. ➢ 质量连续分布刚体的转动惯量 J m ri r m i i d 2 2 = = 质量元: dm 刚体定轴转动的角加速度与它所受的合外力矩成正 比 ,与刚体的转动惯量成反比 . 转动定律 M = J 2 i i J =m r 转动惯量的大小取决于刚体的密度、几何 形状及转轴的位置. 注意
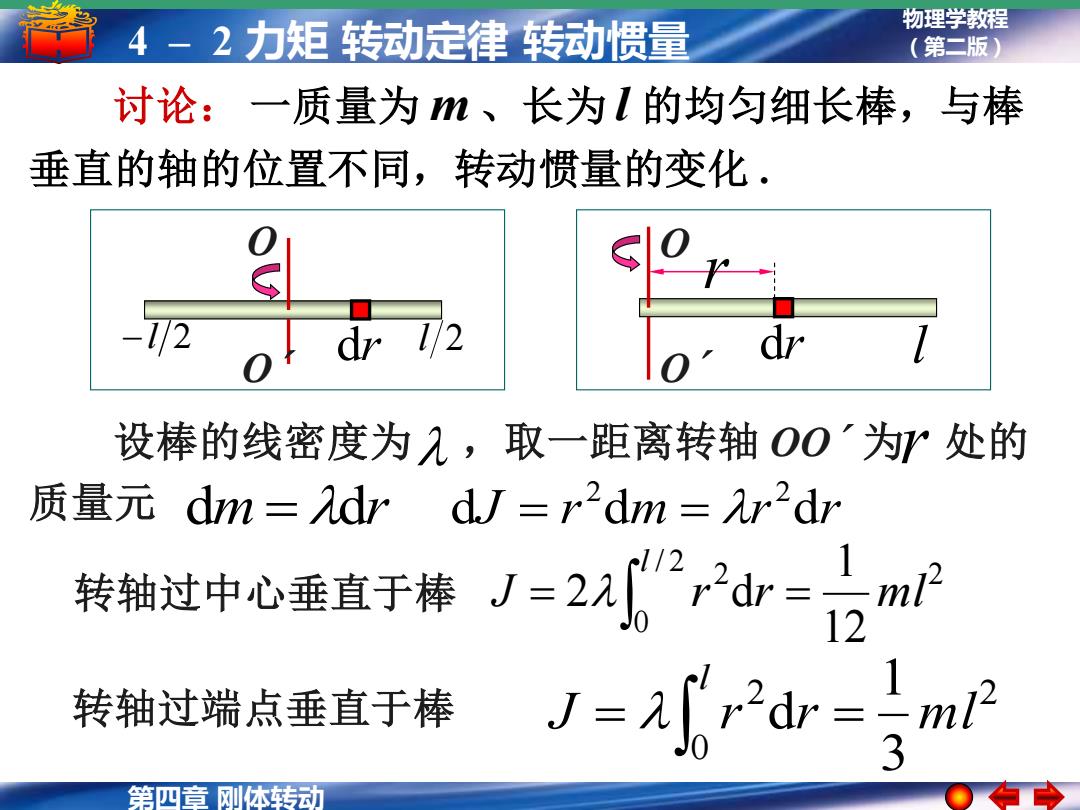
物理学教程 4-2力矩转动定律转动惯量 (第二版) 讨论:一质量为m、长为l的均匀细长棒,与棒 垂直的轴的位置不同,转动惯量的变化 d72 设棒的线密度为1,取一距离转轴O0'为旷处的 质量元dm=λdrdU=r2dm=r2dr 转指过中心宜T掩J=21小”2m 转轴过端点垂直于棒 =02d= 第四章刚体转动
第四章 刚体转动 物理学教程 4 – 2 力矩 转动定律 转动惯量 (第二版) l O´ O dr r 设棒的线密度为 ,取一距离转轴 OO´ 为 处的 质量元 r dm = dr dJ r dm r dr 2 2 = = 讨论: 一质量为 m 、长为 l 的均匀细长棒,与棒 垂直的轴的位置不同,转动惯量的变化 . dr −l 2 l 2 O´ O 2 0 2 3 1 J r dr ml l = = 转轴过端点垂直于棒 2 / 2 0 2 12 1 J 2 r dr ml l = = 转轴过中心垂直于棒
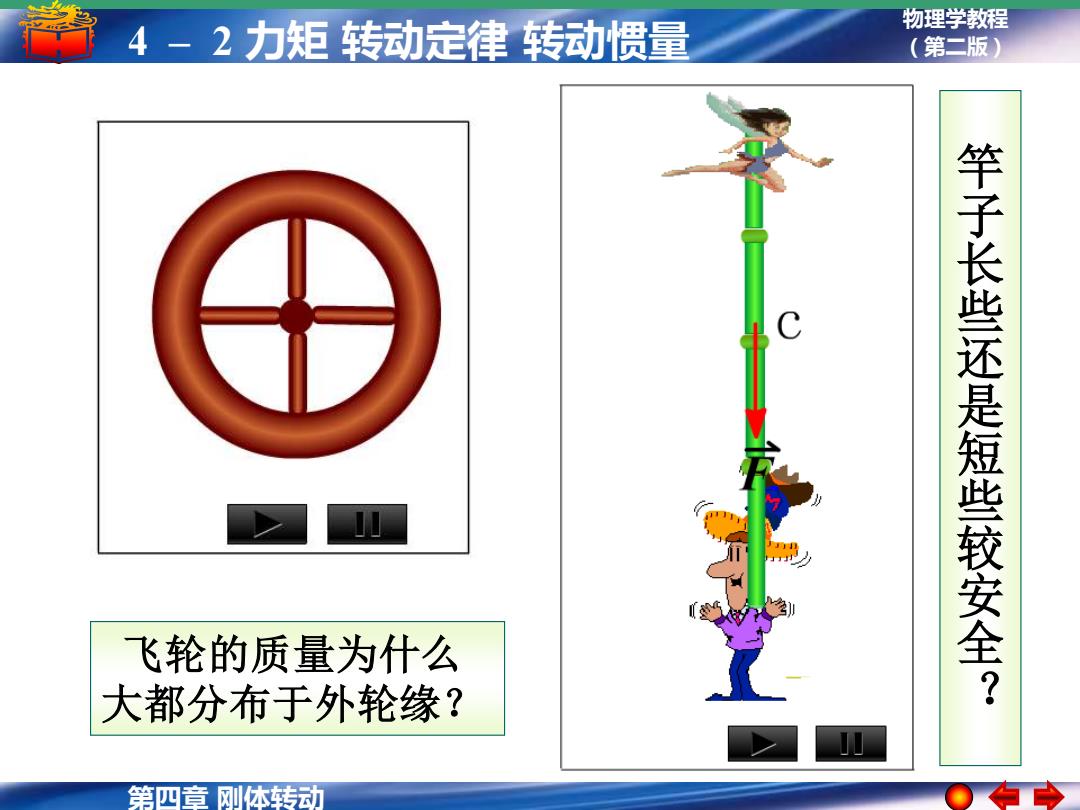
4-2力矩转动定律转动惯量 物理学教程 (第二版) 竿子长些还是短些较安全? 飞轮的质量为什么 大都分布于外轮缘? 第四章刚体转动
第四章 刚体转动 物理学教程 4 – 2 力矩 转动定律 转动惯量 (第二版) 竿子长些还是短些较安全? 飞轮的质量为什么 大都分布于外轮缘?
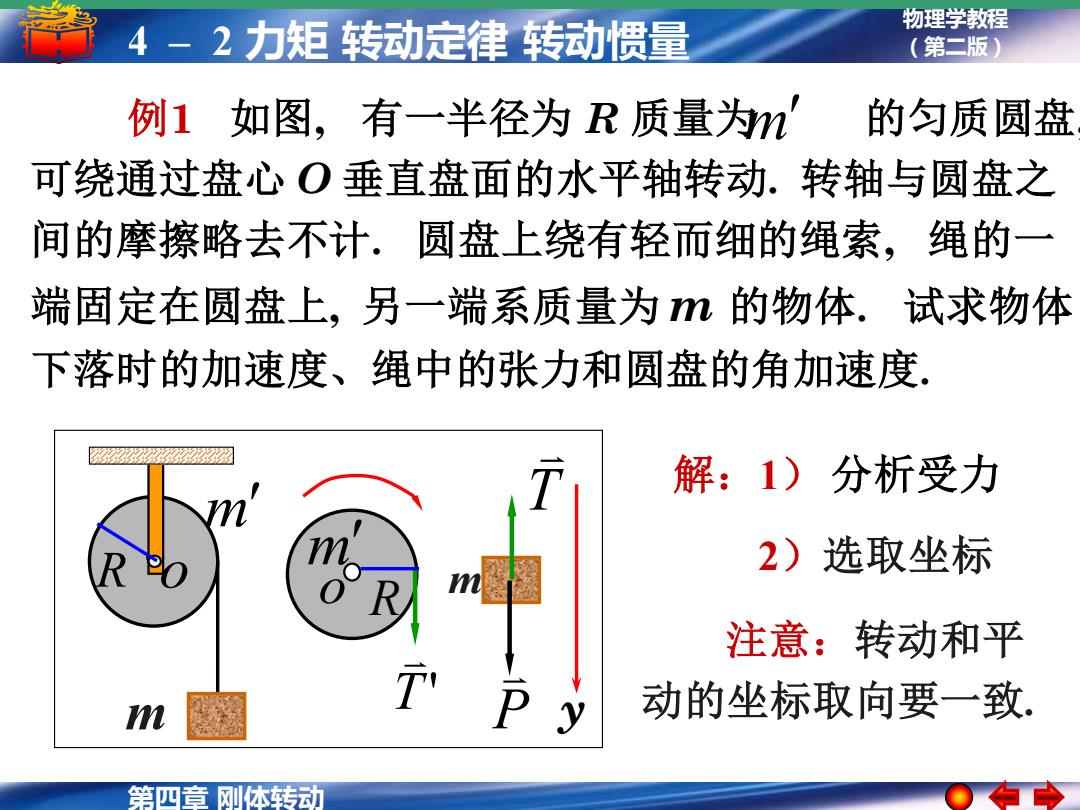
4-2力矩转动定律转动惯量 物理学教程 (第二版) 例1如图,有一半径为R质量为m' 的匀质圆盘 可绕通过盘心O垂直盘面的水平轴转动.转轴与圆盘之 间的摩擦略去不计.圆盘上绕有轻而细的绳索,绳的一 端固定在圆盘上,另一端系质量为的物体.试求物体 下落时的加速度、绳中的张力和圆盘的角加速度. 解:1)分析受力 2)选取坐标 注意:转动和平 动的坐标取向要一致、 第四章刚体转动
第四章 刚体转动 物理学教程 4 – 2 力矩 转动定律 转动惯量 (第二版) 解:1) 分析受力 例1 如图, 有一半径为 R 质量为 的匀质圆盘, 可绕通过盘心 O 垂直盘面的水平轴转动. 转轴与圆盘之 间的摩擦略去不计. 圆盘上绕有轻而细的绳索, 绳的一 端固定在圆盘上, 另一端系质量为 m 的物体. 试求物体 下落时的加速度、绳中的张力和圆盘的角加速度. m R o m m y o R T' m P T m 2)选取坐标 注意:转动和平 动的坐标取向要一致
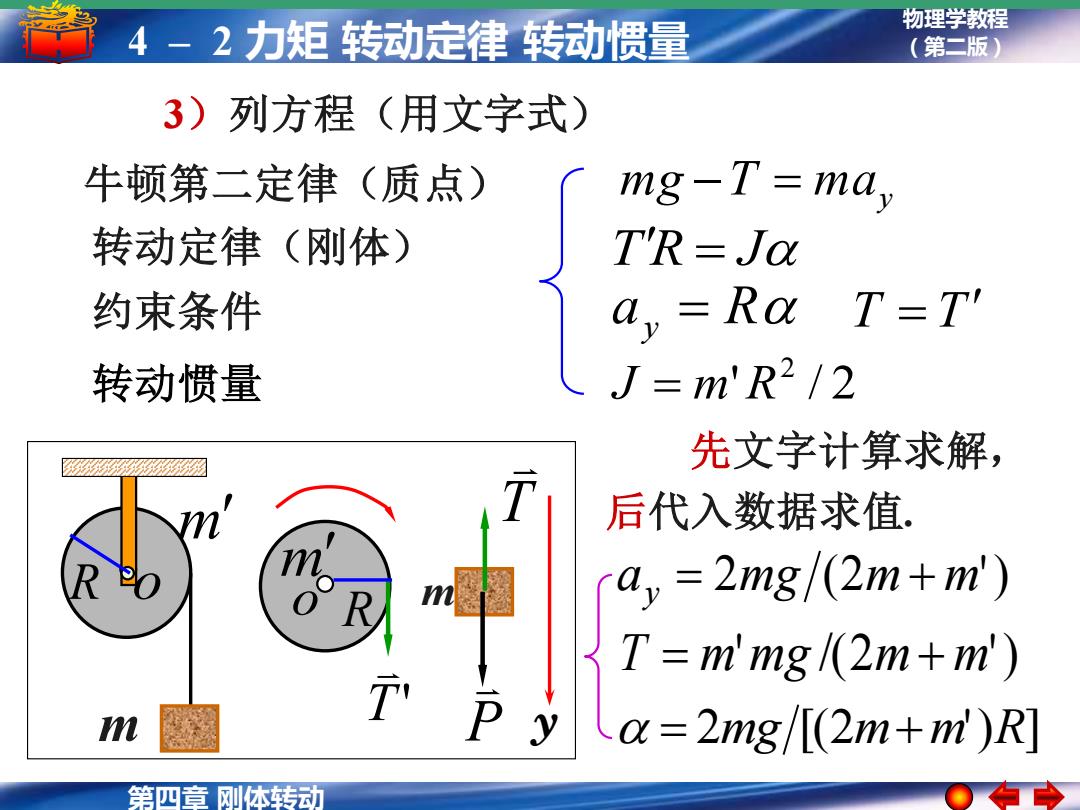
物理学教程 4-2力矩转动定律转动惯量 (第二版) 3)列方程(用文字式) 牛顿第二定律(质点) mg-T=may 转动定律(刚体) TR=Ja 约束条件 ay Ra T=T 转动惯量 J=m'R212 先文字计算求解, 后代入数据求值, m a,=2mg/(2m+m') T=m'mg/(2m+m) T y (a=2mg/[(2m+m)R] 第四章刚体转动
第四章 刚体转动 物理学教程 4 – 2 力矩 转动定律 转动惯量 (第二版) a 2mg (2m m') y = + T = m'mg /(2m + m') = 2mg [(2m+m')R] R o m m y o R T' m P T m 3)列方程(用文字式) 牛顿第二定律(质点) mg −T = may 转动定律(刚体) TR = J ' / 2 2 转动惯量 J = m R 先文字计算求解, 后代入数据求值. 约束条件 ay = R T = T