
6-5驻波 物理学教程 (第二版) 驻波的产生 振幅、频率、传播速度都相同的两列相干波,在 同一直线上沿相反方向传播时叠加而形成的一种特殊 的干涉现象. 基频 三次谐频 三次谐频 四次谐频 第六章机械波
物理学教程 (第二版) 第六章 机械波 6 – 5 驻 波 一 驻波的产生 振幅、频率、传播速度都相同的两列相干波,在 同一直线上沿相反方向传播时叠加而形成的一种特殊 的干涉现象

6-5驻波 物理学教程 (第二版) 实际观察到的弦上的驻波 第六章机械波
物理学教程 (第二版) 第六章 机械波 6 – 5 驻 波 实际观察到的弦上的驻波
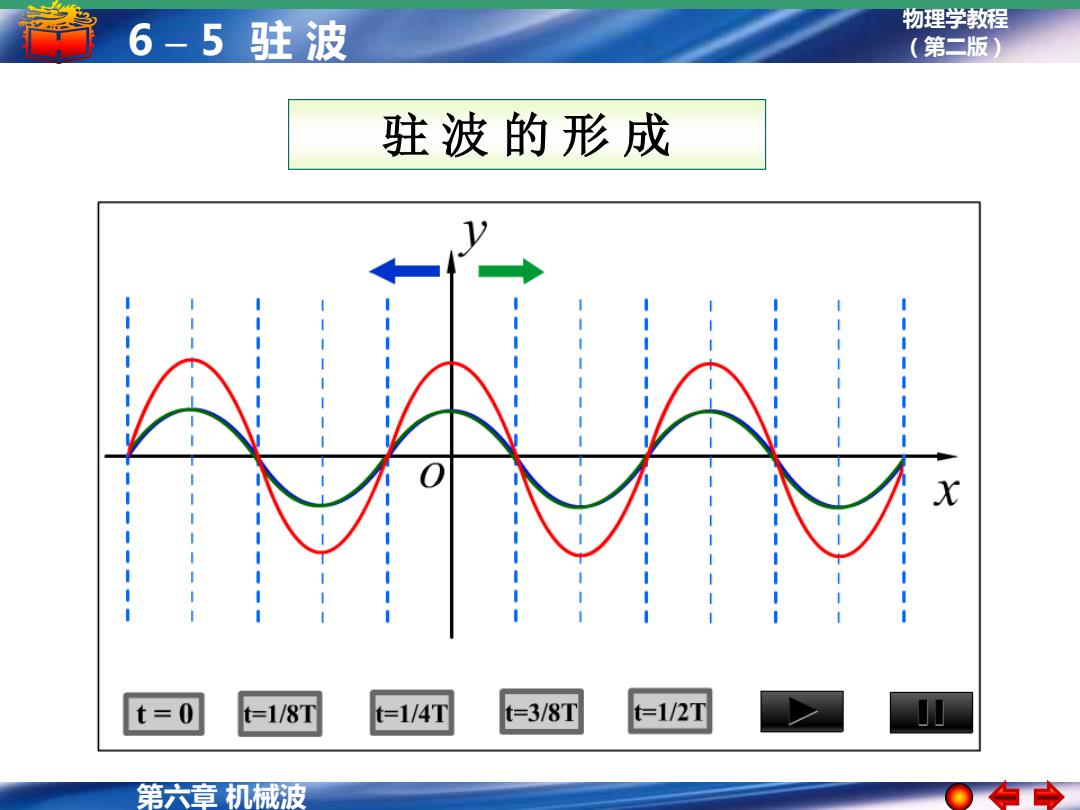
6-5驻波 物理学教程 (第二版) 驻波的形成 t=0 t=1/8T t=1/4T t=3/8T t=1/2T 第六章机械波
物理学教程 (第二版) 第六章 机械波 6 – 5 驻 波 驻 波 的 形 成

6-5驻波 物理学教程 (第二版) 二 驻波方程 正向 乃=4eos2x(1-克 负向,=Acos2xw+子 y=y+y2 =Acos2zx(1-克+Ac0s2r(M+克 =2Ac0s2元 coS2元vt 驻波的振幅 各质点都在作同 与位置有关 频率的简谐运动 第六章机械波
物理学教程 (第二版) 第六章 机械波 6 – 5 驻 波 驻波的振幅 与位置有关 t x A = 2 cos 2π cos 2π 二 驻波方程 cos 2π ( ) 1 x 正向 y = A t − cos 2π ( ) 2 x 负向 y = A t + 1 2 y = y + y 各质点都在作同 频率的简谐运动 cos 2π ( ) cos 2π ( ) x A t x = A t − + +

6-5驻波 物理学教程 (第二版) 讨论 > 驻波方程y=2Ac0S2元,c0S2元t 1)振幅 2Ac0s2元 随x而异,与时间无关, 2π =±kπk=0,1,2,. 2元 -k+m k=0,1,2, ±k k=0,1, 2 Amax =24 波腹 k=0,l,…Amin=0 波节 相邻波腹(节)间距=入/2 相邻波腹和波节间距=几/4 第六章机械波
物理学教程 (第二版) 第六章 机械波 6 – 5 驻 波 t x y A 讨论 ➢ 驻波方程 = 2 cos 2π cos 2π = x cos 2π 2π = k π k = 0,1,2, x )π 0,1,2, 2 1 2π = (k + k = x 1 0 相邻波腹(节)间距 = 2 相邻波腹和波节间距 = 4 1)振幅 随 x 而异, 与时间无关. x 2Acos 2π 波腹 波节 k k 0,1, A 2A 2 = max = 0,1, 0 2 ) 2 1 (k + k = Amin = x =

6-5驻波 物理学教程 (第二版) 2)相邻两波节之间质点振动同相位,任一波节 两侧振动相位相反,在波节处产生兀的相位跃变· (与行波不同,无相位的传播) X y=2Ac0s2πcos2πyt 3入 例X=士 为波节 4 X C0s2元 >0 x<年y=24c0s2r克cos2xW X 4 C0s2π < X , ,=21c0s2元c0S2元M1+元 <X< 4 第六章机械波
物理学教程 (第二版) 第六章 机械波 6 – 5 驻 波 2)相邻两波节之间质点振动同相位,任一波节 两侧振动相位相反,在波节处产生 的相位跃变 . (与行波不同,无相位的传播). π t x y A = 2 cos2π cos2π x cos 2π , 4 4 0, − x t x y A = 2 cos2π cos2π = 2 cos2π cos(2π t +π ) x y A , 4 3 4 0, x x cos 2π 4 例 x = 为波节 x y o 2 2 − 4 4 − 4 3

物理学教程 6-5驻波 (第二版) 三 相位跃变(半波损失) 请观察在反射点入射波和反射波两振动的相位关系 波疏介质较小 波密介质 波密介质较大 当波从波疏介质垂直入射到波密介质,被反射 到波疏介质时形成波节.入射波与反射波在此处的相 位时时相反,即反射波在分界处产生兀的相位跃变, 相当于出现了半个波长的波程差,称半波损失。 第六章机械波
物理学教程 (第二版) 第六章 机械波 6 – 5 驻 波 三 相位跃变(半波损失) 当波从波疏介质垂直入射到波密介质, 被反射 到波疏介质时形成波节. 入射波与反射波在此处的相 位时时相反, 即反射波在分界处产生 的相位跃变, 相当于出现了半个波长的波程差,称半波损失. π 波 密 介 质 u 较 大 波 疏 介 质 较 小 u 请观察在反射点入射波和反射波两振动的相位关系

6-5驻波 物理学教程 (第二版) 请观察在反射点入射波和反射波两振动的相位关系 介质 当波从波密介质垂直入射到波疏介质,被反射 到波密介质时形成波腹.入射波与反射波在此处的相 位时时相同,即反射波在分界处不产生相位跃变 第六章机械波
物理学教程 (第二版) 第六章 机械波 6 – 5 驻 波 当波从波密介质垂直入射到波疏介质, 被反射 到波密介质时形成波腹. 入射波与反射波在此处的相 位时时相同,即反射波在分界处不产生相位跃变. 请观察在反射点入射波和反射波两振动的相位关系
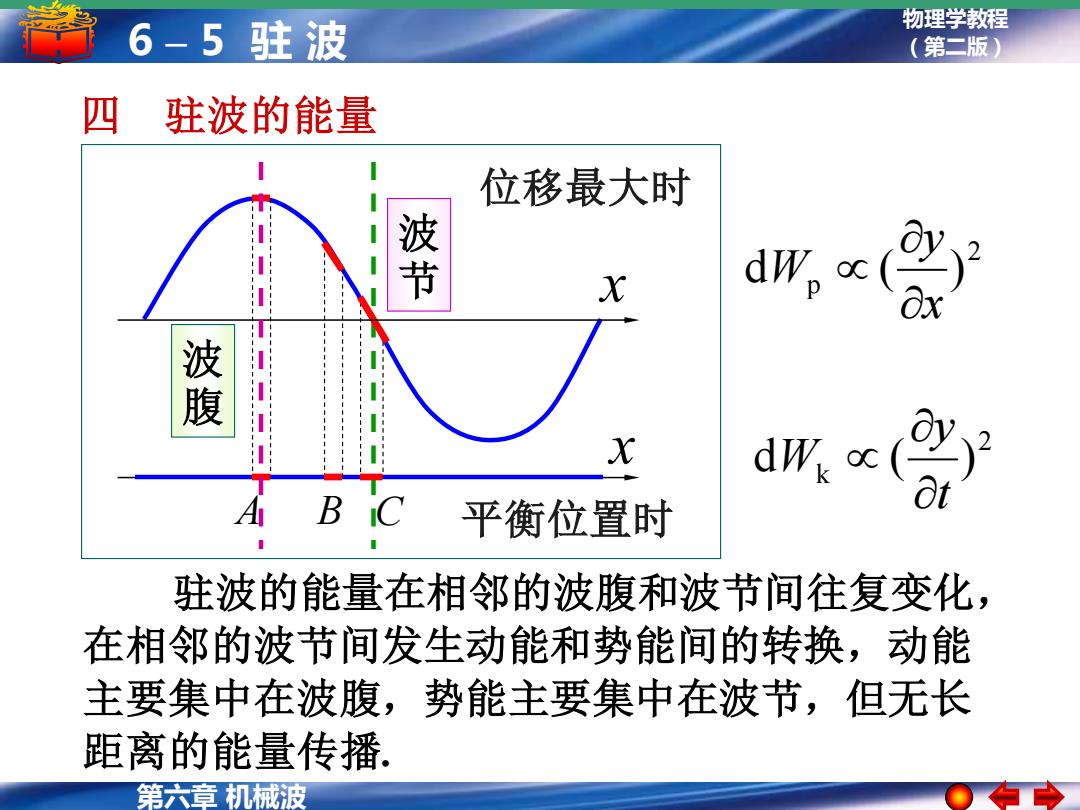
6-5驻波 物理学教程 (第二版) 四 驻波的能量 位移最大时 波 X dw, 谈 X dx( A B C 平衡位置时 驻波的能量在相邻的波腹和波节间往复变化, 在相邻的波节间发生动能和势能间的转换,动能 主要集中在波腹,势能主要集中在波节,但无长 距离的能量传播 第六章机械波
物理学教程 (第二版) 第六章 机械波 6 – 5 驻 波 四 驻波的能量 2 k d ( ) t y W 2 p d ( ) x y W 驻波的能量在相邻的波腹和波节间往复变化, 在相邻的波节间发生动能和势能间的转换,动能 主要集中在波腹,势能主要集中在波节,但无长 距离的能量传播. A B C 波 节 波 腹 x x 位移最大时 平衡位置时

6-5驻波 物理学教程 (第二版) 例已知一根线上的驻波方程为 y=0.040sin5元xcos40πt 1)求在0≤x≤0.40m内所有波节的位置 解由sn5πx=0得5πx=k元(k=0,12…) 则x=二k所以,波节为: 5 x1=0m,x2=0.20m,x3=0.40m 2)求线上除波节点之外的任意点的振动周期是多少? 解驻波的波节点不动,其它各点以相同的周期 振动 由2元y=40元 得V=20Hz T=0.05s 第六章机械波
物理学教程 (第二版) 第六章 机械波 6 – 5 驻 波 例 已知一根线上的驻波方程为 y = 0.040sin 5π x cos 40 πt 1)求在 0 x 0.40m 内所有波节的位置. 解 由 sin 5π x = 0 得 5π x = k π (k = 0,1,2) 则 x k 5 1 = 所以,波节为: 0m, 0.20m, 0.40m. x1 = x2 = x3 = 2)求线上除波节点之外的任意点的振动周期是多少? 由 2 π = 40π 得 = 20Hz T = 0.05s 驻波的波节点不动,其它各点以相同的周期 振动 解