
刚体的转动内容提要 物理学教程 (第二版) 一.刚体的定轴转动匀变速转动 0=0+0t 1 0=0+ot+5at2 2 w2=@,2+2(0-0)) 2 二.刚体的定轴转动定律 刚体定轴转动的角加速度与它所受的合外力矩成 正比,与刚体的转动惯量成反比. M=Jo 刚体转动惯量 J=∑△m,g2J=「rdm 第四章刚体转动
第四章 刚体转动 物理学教程 刚体的转动内容提要 (第二版) 一. 刚体的定轴转动 匀变速转动 = +t 0 2 0 0 2 1 = + t + t 2 ( ) 0 2 0 2 = + − 二. 刚体的定轴转动定律 刚体定轴转动的角加速度与它所受的合外力矩成 正比,与刚体的转动惯量成反比 . M = J ➢ 刚体转动惯量 J r dm 2 = = 2 i i J m r

刚体的转动内容提要 物理学教程 (第二版) 三.刚体定轴转动功和能 力矩的功 Mdo 1 > 转动动能 重力势能 Ep =mghc > 刚体定轴转动的动能定理 w=M0-号w-2® 刚体的机械能守恒定律:若只有保守力做功时, 则E,+E=恒量 第四章刚体转动
第四章 刚体转动 物理学教程 刚体的转动内容提要 (第二版) ➢ 刚体定轴转动的动能定理 2 1 2 2 2 1 2 1 d 2 1 W = M = J − J 三. 刚体定轴转动功和能 = 2 1 d ➢ 力矩的功 W M ➢ 转动动能 2 k 2 1 E = J ➢ 重力势能 EP = mghC ➢ 刚体的机械能守恒定律:若只有保守力做功时, 则 EP + Ek = 恒量

刚体的转动内容提要 物理学教程 (第二版) 四.刚体定轴转动的角动量定理和角动量守恒定律 > 刚体对转轴的角动量: L=Jo M= dL d(Jo) 角动量定理: dt dt Mdt J2@2-J@ >角动量守恒定律若M=0,则L=Jo=常量 五定轴转动的动力学问题解题基本步骤 首先分析各物体所受力和力矩情况,然后根据已 知条件和所求物理量判断应选用的规律,最后列方程 求解 第四章刚体转动
第四章 刚体转动 物理学教程 刚体的转动内容提要 (第二版) 四. 刚体定轴转动的角动量定理和角动量守恒定律 ➢ 刚体对转轴的角动量: L = J t J t L M d d( ) d d ➢ 角动量定理: = = 2 2 1 1 2 1 Mdt J J t t = − ➢ 角动量守恒定律 若 M = 0 ,则 L = J =常量 首先分析各物体所受力和力矩情况,然后根据已 知条件和所求物理量判断应选用的规律,最后列方程 求解. 五 定轴转动的动力学问题 解题基本步骤

刚体的转动内容提要 物理学教程 (第二版) 1.求刚体转动某瞬间的角加速度,一般应用转动 定律求解。如质点和刚体组成的系统,对质点列牛顿 运动方程,对刚体列转动定律方程,再列角量和线量 的关联方程,联立求解, 2.刚体与质点的碰撞、打击问题,在有心力场作 用下绕力心转动的质点问题,考虑用角动量守恒定律. 3.在刚体所受的合外力矩不等于零时,比如木杆 摆动,受重力矩作用,一般应用刚体的转动动能定理 或机械能守恒定律求解。 另外:实际问题中常常有多个复杂过程,要分成 几个阶段进行分析,分别列出方程,进行求解。 第四章刚休转动
第四章 刚体转动 物理学教程 刚体的转动内容提要 (第二版) 1. 求刚体转动某瞬间的角加速度,一般应用转动 定律求解。如质点和刚体组成的系统,对质点列牛顿 运动方程,对刚体列转动定律方程,再列角量和线量 的关联方程,联立求解. 2. 刚体与质点的碰撞、打击问题,在有心力场作 用下绕力心转动的质点问题,考虑用角动量守恒定律. 另外:实际问题中常常有多个复杂过程,要分成 几个阶段进行分析,分别列出方程,进行求解. 3. 在刚体所受的合外力矩不等于零时,比如木杆 摆动,受重力矩作用,一般应用刚体的转动动能定理 或机械能守恒定律求解
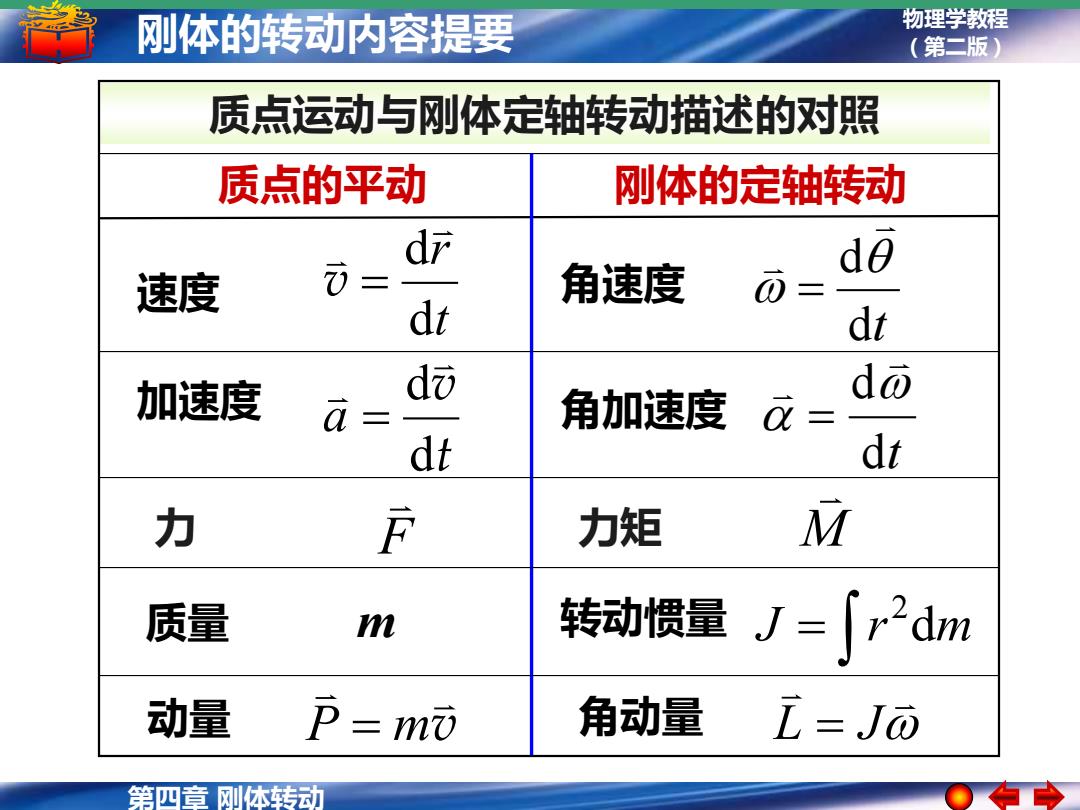
刚体的转动内容提要 物理学教程 (第二版) 质点运动与刚体定轴转动描述的对照 质点的平动 刚体的定轴转动 dr )= do 速度 角速度 dt dt 加速度 d而 do a- 角加速度 a= dt dt 力 京 力矩 M 质量 m 转动惯量J=∫r2dm 动量 P=mi 角动量 i=Jò 第四章刚体转动
第四章 刚体转动 物理学教程 刚体的转动内容提要 (第二版) 质点运动与刚体定轴转动描述的对照 质点的平动 刚体的定轴转动 速度 加速度 t r d d v = t v d d a = 角速度 角加速度 dt d = dt d = 质量 m 转动惯量 动量 角动量 J r dm 2 = v L = J P = m 力 F 力矩 M

刚体的转动内容提要 物理学教程 (第二版) 质点运动规律与刚体定轴转动的规律对照 质点的平动 刚体的定轴转动 运动定律 F=ma 转动定律 M=Ja 动量定理 角动量定理 dt=mi-mi。 -乙- 动量守恒定律 角动量守恒定律 ∑万=0,∑m0,=恒量 M=0,∑J,@,=恒量 力的功 W=心F.d 力矩的功 W=Md6 动能 Ek=m2/2 转动动能 Ex=Jo2/2 第四章刚体转动
第四章 刚体转动 物理学教程 刚体的转动内容提要 (第二版) 质点运动规律与刚体定轴转动的规律对照 运动定律 F ma = 转动定律 M = J 质点的平动 刚体的定轴转动 动量定理 0 0 d v v F t m m t t = − 角动量定理 0 0 Mdt L L t t = − 动量守恒定律 角动量守恒定律 Fi = mi vi = 恒量 0, M = Ji i = 恒量 0, 力的功 = b a W F r d 力矩的功 = 0 W Md 动能 / 2 2 Ek = mv 转动动能 / 2 2 Ek = J

刚体的转动内容提要 物理学教程 (第二版) 质点运动规律与刚体定轴转动的规律对照 质点的平动 刚体的定轴转动 动能定理 动能定理 W= mo2 mvo 2 2 2 重力势能 Ep=mgh 重力势能 Ep=mgho 机械能守恒 机械能守恒 只有保守力作功时 只有保守力作功时 Ek十E。=恒量 Ek+E。=恒量 第四章刚体转动
第四章 刚体转动 物理学教程 刚体的转动内容提要 (第二版) 质点运动规律与刚体定轴转动的规律对照 质点的平动 刚体的定轴转动 动能定理 2 0 2 2 1 2 1 W = mv − mv 动能定理 2 0 2 2 1 2 1 W = J − J 重力势能 Ep = mgh 重力势能 Ep = mghC 机械能守恒 Ek + Ep = 恒量 只有保守力作功时 机械能守恒 Ek + Ep = 恒量 只有保守力作功时