物理学教程 4-1刚体的定轴转动 (第二版) 刚体的平动与转动 > 刚体:在外力作用下,形状和大小都不发生变化 的物体.(任意两质点间距离保持不变的特殊质点组) 刚体的运动形式:平动、转动 > 平动:若刚体中所有点 的运动轨迹都保持完全相同, 或者说刚体内任意两点间的 连线总是平行于它们的初始 位置间的连线. 刚体平动>质点运动 第四章刚体转动
第四章 刚体转动 物理学教程 4 – 1 刚体的定轴转动 (第二版) ➢ 刚体:在外力作用下,形状和大小都不发生变化 的物体. (任意两质点间距离保持不变的特殊质点组) 刚体的运动形式:平动、转动. 刚体平动 质点运动 ➢ 平动:若刚体中所有点 的运动轨迹都保持完全相同, 或者说刚体内任意两点间的 连线总是平行于它们的初始 位置间的连线. 一 刚体的平动与转动
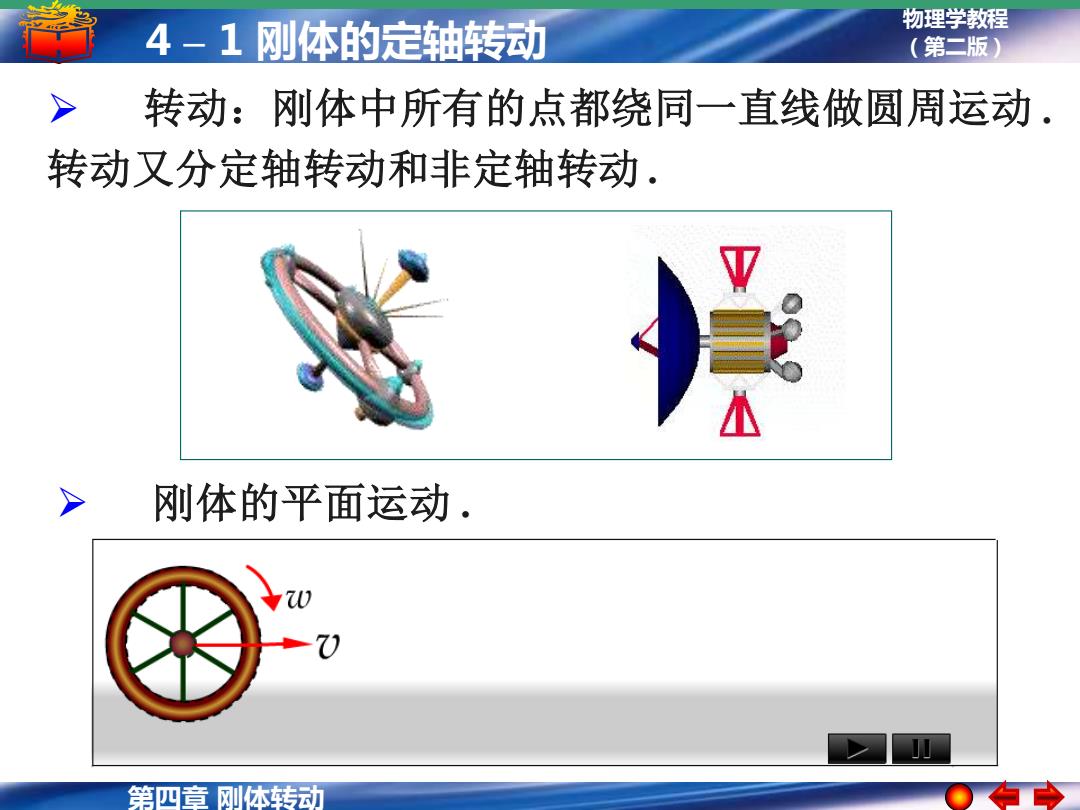
4-1刚体的定轴转动 物理学教程 (第二版) > 转动:刚体中所有的点都绕同一直线做圆周运动. 转动又分定轴转动和非定轴转动. 刚体的平面运动. 第四章刚体转动
第四章 刚体转动 物理学教程 4 – 1 刚体的定轴转动 (第二版) ➢ 转动:刚体中所有的点都绕同一直线做圆周运动 . 转动又分定轴转动和非定轴转动 . ➢ 刚体的平面运动

物理学教程 4-1刚体的定轴转动 (第二版) >刚体的一般运动 质心的平动 十绕质心的转动 第四章刚体转动
第四章 刚体转动 物理学教程 4 – 1 刚体的定轴转动 (第二版) ➢ 刚体的一般运动 质心的平动 + 绕质心的转动

物理学教程 4-1刚体的定轴转动 (第二版) 二 刚体绕定轴转动的角速度和角加速度 1角速度和角加速度 0(t) > 。角坐标0=0(t) ◆ 约定 沿逆时针方向转动0>0 沿顺时针方向转动0 角速度矢量w=lim △t>0 △t dt ®方向:右手螺旋方向 第四章刚体转动
第四章 刚体转动 物理学教程 4 – 1 刚体的定轴转动 (第二版) z x 二 刚体绕定轴转动的角速度和角加速度 参考平面 ➢ 角位移 =(t + t) −(t) ➢ 角坐标 = (t) 0 约定 沿逆时针方向转动 沿顺时针方向转动 t t t d d lim 0 = = → ➢ 角速度矢量 方向: 右手螺旋方向 参考轴 1 角速度和角加速度 (t)
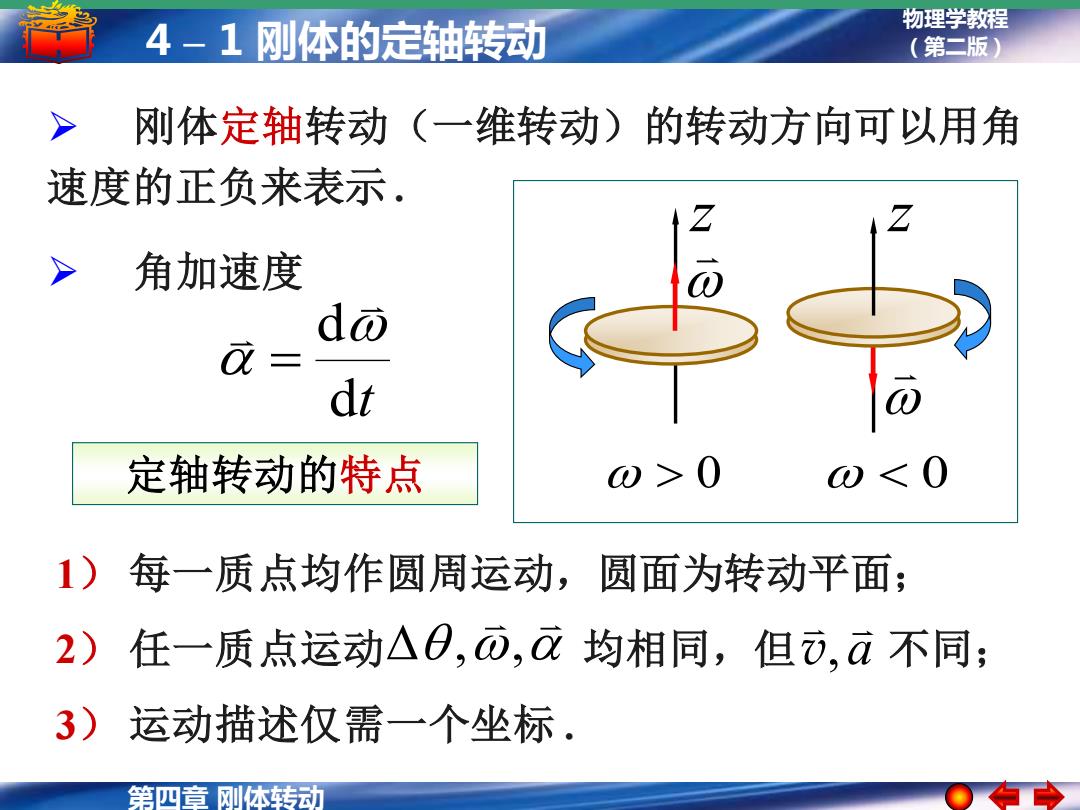
物理学教程 4-1刚体的定轴转动 (第二版) > 刚体定轴转动(一维转动)的转动方向可以用角 速度的正负来表示. 角加速度 d = dt 定轴转动的特点 o>0 )<0 1)每一质点均作圆周运动,圆面为转动平面; 2)任一质点运动△0,而,均相同,但方,a不同; 3) 运动描述仅需一个坐标. 第四章刚体转动
第四章 刚体转动 物理学教程 4 – 1 刚体的定轴转动 (第二版) ➢ 角加速度 dt d = 1) 每一质点均作圆周运动,圆面为转动平面; 2) 任一质点运动 均相同,但 不同; 3) 运动描述仅需一个坐标 . , , a v, 定轴转动的特点 ➢ 刚体定轴转动(一维转动)的转动方向可以用角 速度的正负来表示 . > 0 < 0 z z

4-1刚体的定轴转动 物理学教程 (第二版) 2匀变速转动公式 当刚体绕定轴转动的角加速度为恒量时,刚体做 匀变速转动. 刚体匀变速转动与质点匀变速直线运动公式对比 质点匀变速直线运动 刚体绕定轴作匀变速转动 0=)0+at ①=⊙,+Ot x=x0+xot+2at20=0,+0,t+5at2 z2=v+2a(x-x)o2=w+2(0-0) 第四章刚体转动
第四章 刚体转动 物理学教程 4 – 1 刚体的定轴转动 (第二版) 2 匀变速转动公式 质点匀变速直线运动 刚体绕定轴作匀变速转动 = + at v v0 2 2 1 x = x0 + v0 t + at 2 ( ) 0 2 0 2 v = v + a x − x = +t 0 2 ( ) 0 2 0 2 = + − 2 2 1 0 0 = + t + t 当刚体绕定轴转动的角加速度为恒量时,刚体做 匀变速转动 . 刚体匀变速转动与质点匀变速直线运动公式对比

物理学教程 4-1刚体的定轴转动 (第二版) 3角量与线量的关系 do 0 dt d20 e, do Q= dt _d2t roe a -ra 2 a rae,+ra2e. n =r0 第四章刚体转动
第四章 刚体转动 物理学教程 4 – 1 刚体的定轴转动 (第二版) 3 角量与线量的关系 et r v = r t e v 2 n t a r a r = = t a n a n 2 t a r e r e = + dt d = t t 2 2 d d d d = = a

物理学教程 4-1刚体的定轴转动 (第二版) 例1一飞轮半径为0.2m、转速为150 rmin-,因 受制动而均匀减速,经30s停止转动. 试求:(1)角加速度和在此时间内飞轮所转的圈数; 解(1)w=5πrads1,t=30s时,o=0. 设t=0s时,O,=0.飞轮做匀减速运动 Q= 0-000-5元 -rad.s-2 30 飞轮30s内转过的角度 0-. 02- 2 -(5π)2 =75元rad 20 2×(-元/6) 转过的圈数N=0/2元=37.5r 第四章刚体转动
第四章 刚体转动 物理学教程 4 – 1 刚体的定轴转动 (第二版) 飞轮 30 s 内转过的角度 75π rad 2 ( π 6) (5π ) 2 2 2 0 2 = − − = − = 0 2 rad s 6 π 30 0 5π − = − − = − = t 例1 一飞轮半径为 0.2m、 转速为150r·min-1 , 因 受制动而均匀减速,经 30 s 停止转动 . 试求:(1)角加速度和在此时间内飞轮所转的圈数; 解 (1) 5π rad s , 1 0 − = t = 30 s 时, = 0. 设 t = 0 s时, 0 = 0.飞轮做匀减速运动 转过的圈数 N = 2 π = 37.5 r

物理学教程 4-1刚体的定轴转动 (第二版) 已知:o=5元rads1,r=0.2m.求: (2)制动开始后t=6s时飞轮的角速度; 解:W=@+M=6元-6×6)=4元rads (3)t=6s时飞轮边缘上一点的线速度、切向加速 度和法向加速度. 解:)=r0=0.2×4元=2.5mS2 a=a=0.2x(-君=-0.105ms an=rw2=0.2×(4元)2=31.6ms2 第四章刚体转动
第四章 刚体转动 物理学教程 4 – 1 刚体的定轴转动 (第二版) 1 0 6) 4 π rad s 6 π (5π − = +t = − = 2 t ) 0.105 m s 6 π 0.2 ( − a = r = − = − 2 2 2 n 0.2 (4 π) 31.6 m s − a = r = = (2)制动开始后t = 6 s 时飞轮的角速度; (3)t = 6 s 时飞轮边缘上一点的线速度、切向加速 度和法向加速度 . 解: 5πrad s , 0.2m 1 0 = = − 已知: r . 求: 2 0.2 4π 2.5 m s − 解: v = r = =

物理学教程 4-1刚体的定轴转动 (第二版) 例2在高速旋转的微型电机里,有一圆柱形转子可绕 垂直其横截面并通过中心的转轴旋转.开始起动时,角速度 为零.起动后其转速随时间变化关系为:0=om(1-e/), 式中0m=540r/S,t=2.0s.求:(1)t=6s时电动机 的转速.(2)起动后,电动机在t=6s时间内转过的圈数 (3)角加速度随时间变化的规律. 解:(1)将t=6s代入得0=0.95ωm=513r/S ()ddi do=@me=540me-2rad.s-2 (角加速度 (3) 0= dt 2入 指数衰减) 第四章刚体转动
第四章 刚体转动 物理学教程 4 – 1 刚体的定轴转动 (第二版) 例2 在高速旋转的微型电机里, 有一圆柱形转子可绕 垂直其横截面并通过中心的转轴旋转. 开始起动时, 角速度 为零. 起动后其转速随时间变化关系为: , 式中 . 求:(1) t = 6s 时电动机 的转速.(2)起动后, 电动机在 t = 6s 时间内转过的圈数. (3)角加速度随时间变化的规律. (1 ) / t m e − = − = 540r/s, = 2.0s m (2) 解: (1) 将 t = 6s 代入得 = 0 95 = 513 r/s ωm ω . − = = − 6 0 6 0 / (1 )d 2π 1 d 2π 1 N t e t t m (3) / / 2 2 540π rad s d d − − − = = = m t t e e t = 344 (角加速度 指数衰减)