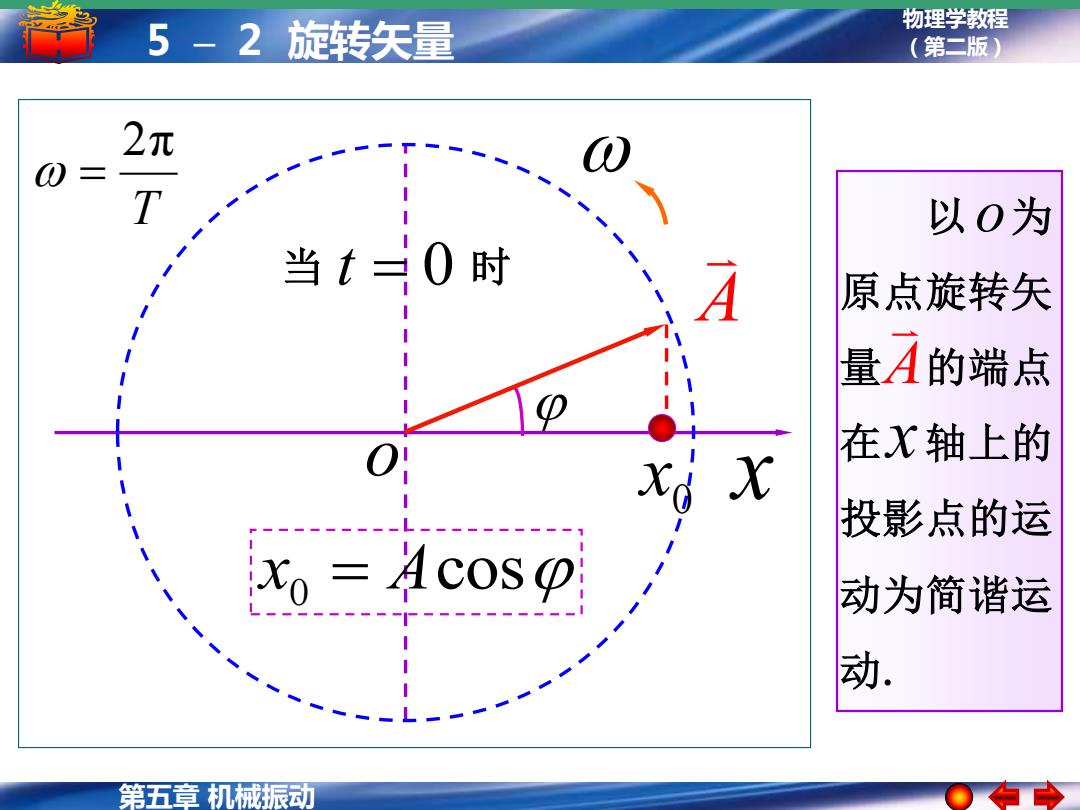
5-2旋转矢量 物理学教程 (第二版) 2元 T 以0为 当t三0时 A 原点旋转矢 量A的端点 在X轴上的 xd X 投影点的运 ixo Acosp 动为简谐运 动. 第五章机械振动
物理学教程 5 – 2 旋转矢量 (第二版) 第五章 机械振动 以 为 原点旋转矢 量 的端点 在 轴上的 投影点的运 动为简谐运 动. x A o x o A x0 = Acos 当 t = 0 时 0 x T 2π =
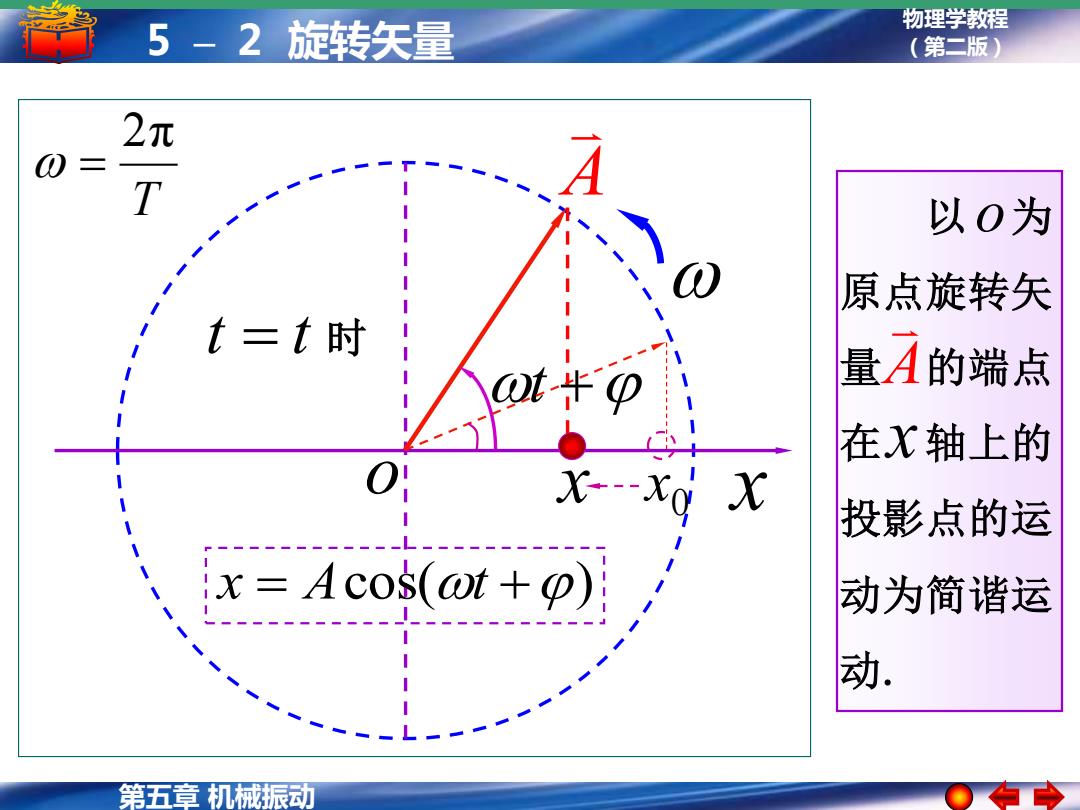
5-2旋转矢量 物理学教程 (第二版) 2元 T A 以0为 原点旋转矢 t =t时 量A的端点 在X轴上的 X---Xo X 投影点的运 x=Acos(ot+p) 动为简谐运 动. 第五章机械振动
物理学教程 5 – 2 旋转矢量 (第二版) 第五章 机械振动 以 为 原点旋转矢 量 的端点 在 轴上的 投影点的运 动为简谐运 动. x A o o x A t = t t + 时 x 0 x T 2π = x = Acos(t +)
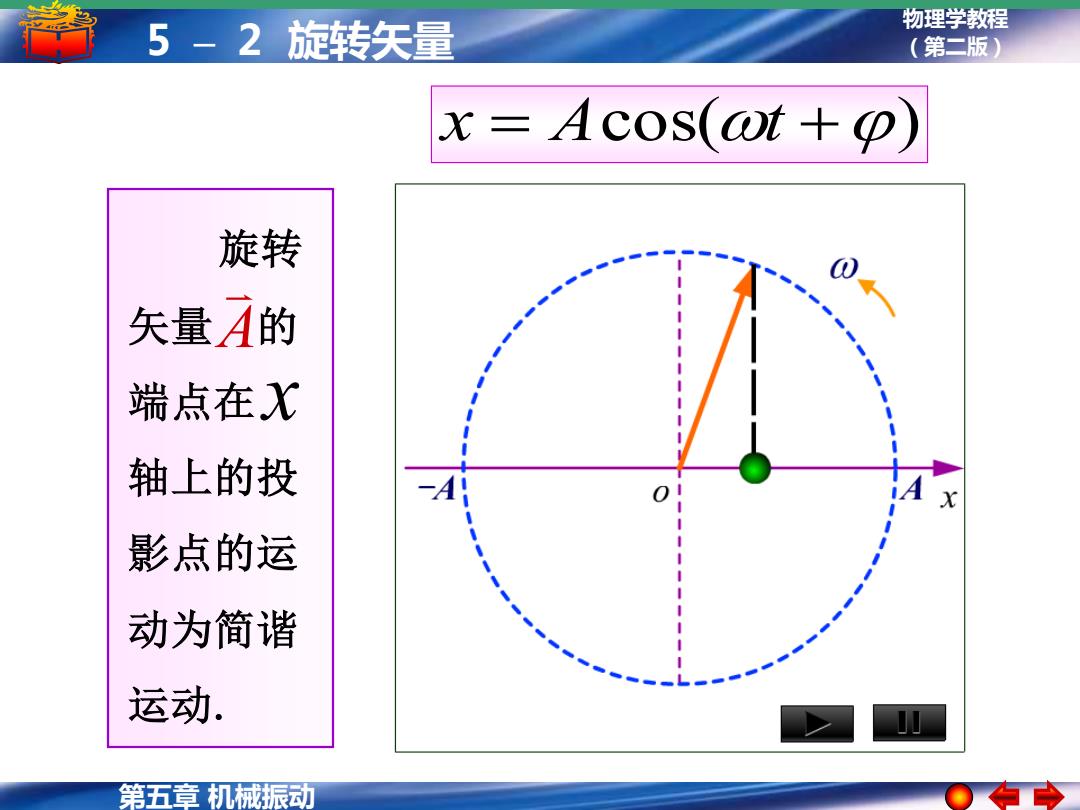
5-2旋转矢量 物理学教程 (第二版) x=Acos(at+p) 旋转 矢量A的 端点在X 轴上的投 影点的运 动为简谐 运动. 第五章机械振动
物理学教程 5 – 2 旋转矢量 (第二版) 第五章 机械振动 x = Acos(t +) 旋转 矢量 的 端点在 轴上的投 影点的运 动为简谐 运动. x A

5-2旋转矢量 物理学教程 (第二版) m 元 ot+0 2 Um -A@ ωt+D a Aw X x=Acos(@t+p) A@cos(ot+p+ 2 a=-Aw-cos(ot+o) 第五章机械振动
物理学教程 5 – 2 旋转矢量 (第二版) 第五章 机械振动 vm = A ) 2 π v = A cos(t + + cos( ) 2 a = −A t + 2 an = A 2 π t + + vm v x y 0 A t + x = Acos(t +) n a a
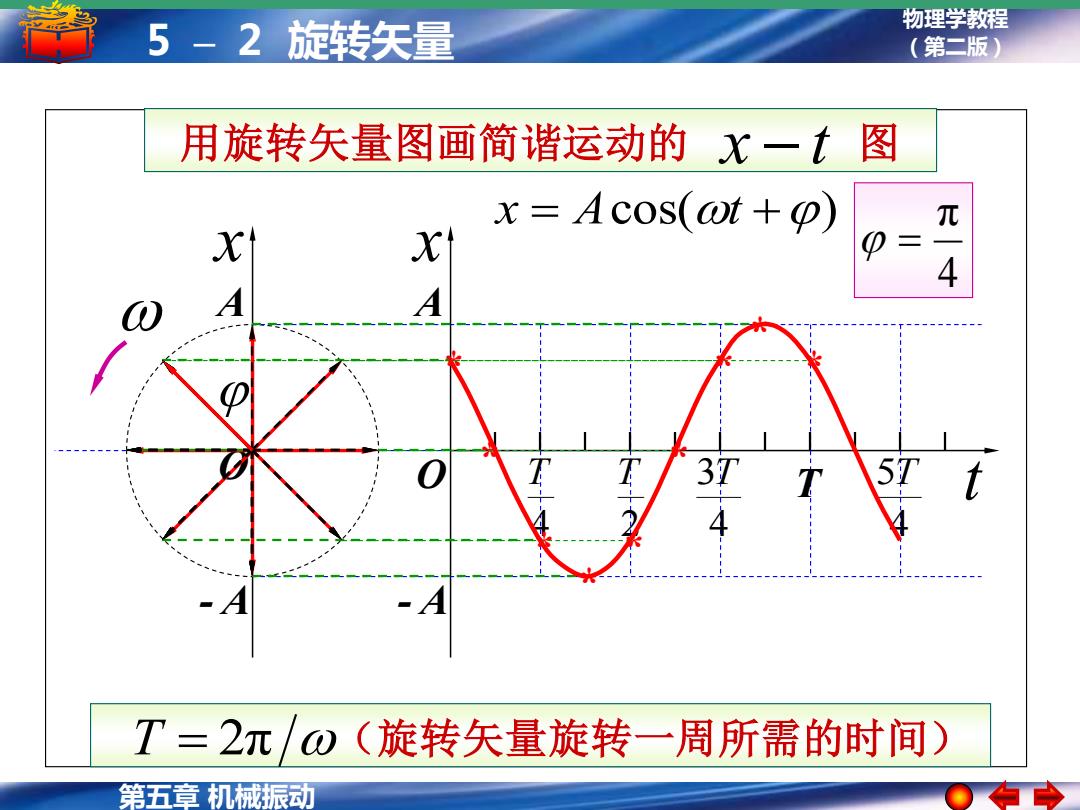
5-2旋转矢量 物理学教程 (第二版) 用旋转矢量图画简谐运动的尤一图 x=Acos(ot+o) 元 4 T=2π/ω(旋转矢量旋转一周所需的时间) 第五章机械振动
物理学教程 5 – 2 旋转矢量 (第二版) 第五章 机械振动 A - A O O T 2 T 4 T 4 3T 4 5T * x x t A - A 用旋转矢量图画简谐运动的 x − t 图 (旋转矢量旋转一周所需的时间) * * * * * * * * T = 2π 4 π = x = Acos(t +)
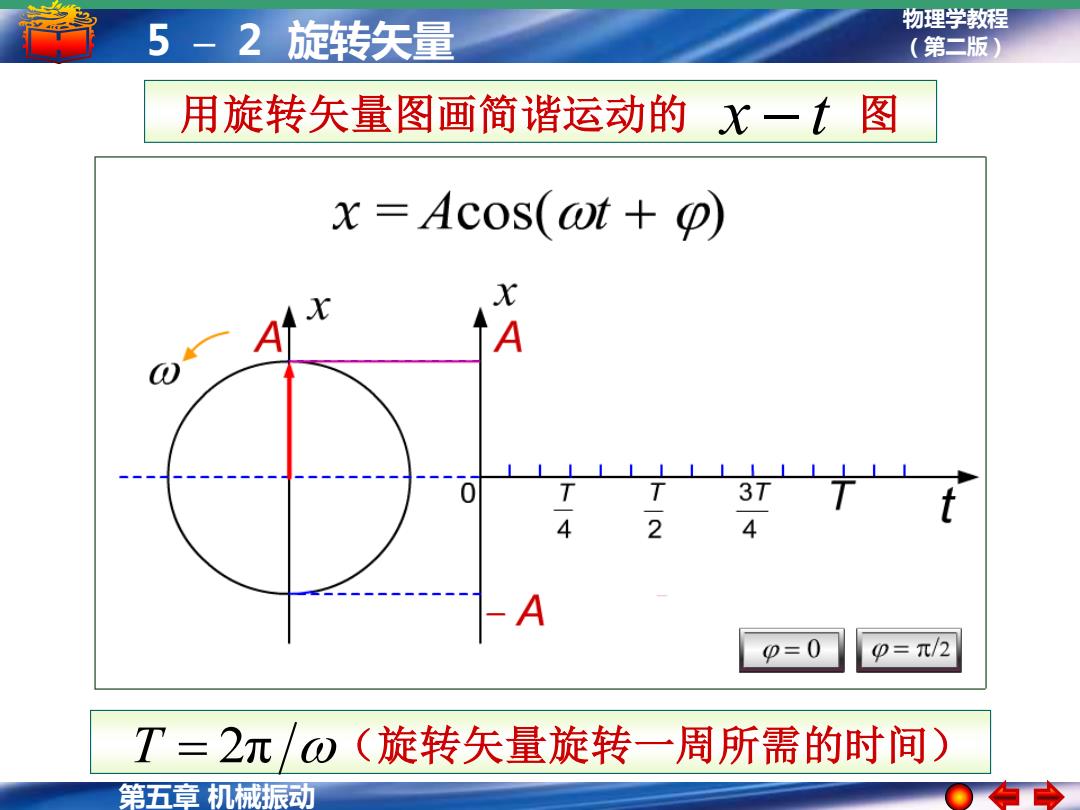
5-2旋转矢量 物理学教程 (第二版) 用旋转矢量图画简谐运动的飞一t图 x=Acos(ot+o) X A A 37 A p=0 p=π/2 T=2元/0(旋转矢量旋转一周所需的时间) 第五章机械振动
物理学教程 5 – 2 旋转矢量 (第二版) 第五章 机械振动 T = 2π (旋转矢量旋转一周所需的时间) 用旋转矢量图画简谐运动的 x − t 图
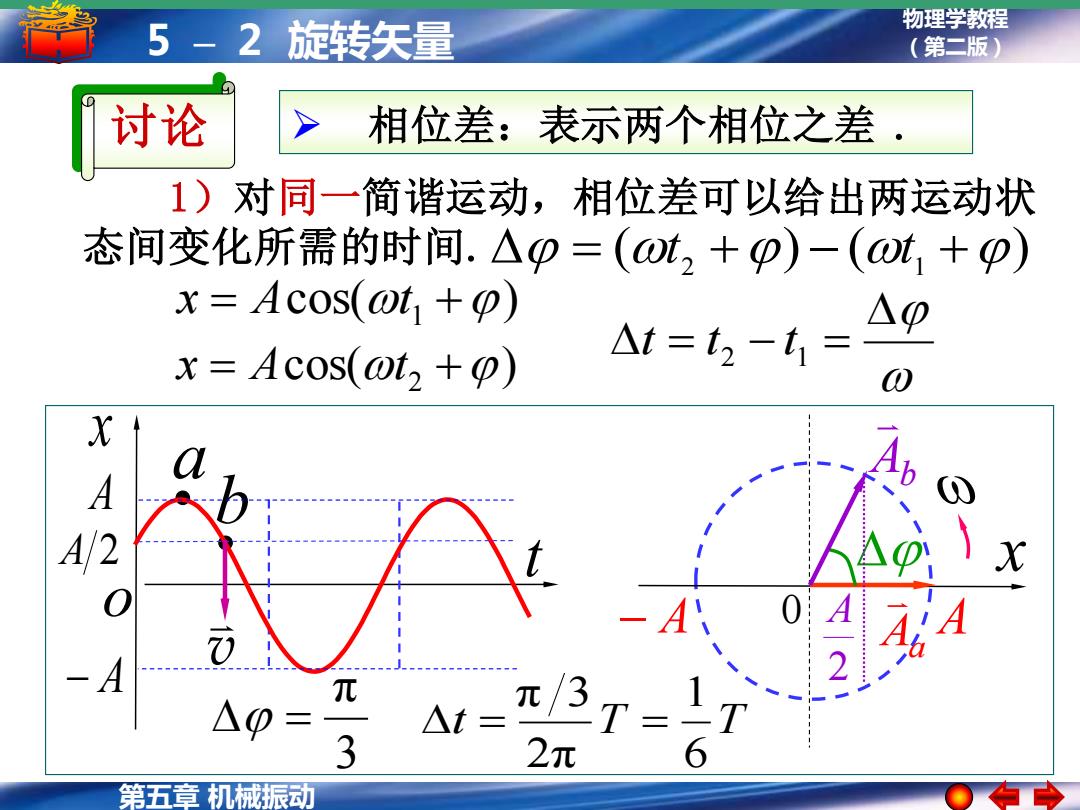
-2旋转矢量 物理学教程 (第二版) 讨论 相位差:表示两个相位之差 . 1)对同一简谐运动,相位差可以给出两运动状 态间变化所需的时间.△p=(⊙t2+p)-(ot,+p) x=Acos(@t+) △p x=Acos(@t,+) △t=t2-t1= 0 X A A/2 7 △0= △t= 3 2元 第五章机械振动
物理学教程 5 – 2 旋转矢量 (第二版) 第五章 机械振动 A − A x A 2 t o a b x − A 0 A 讨论 ➢ 相位差:表示两个相位之差 . 1)对同一简谐运动,相位差可以给出两运动状 态间变化所需的时间. ( ) ( ) = t 2 + − t 1 + cos( ) x = A t 1 + cos( ) x = A t 2 + t = t 2 − t 1 = Aa 3 π = t T T 6 1 2π π 3 = = v 2 A Ab
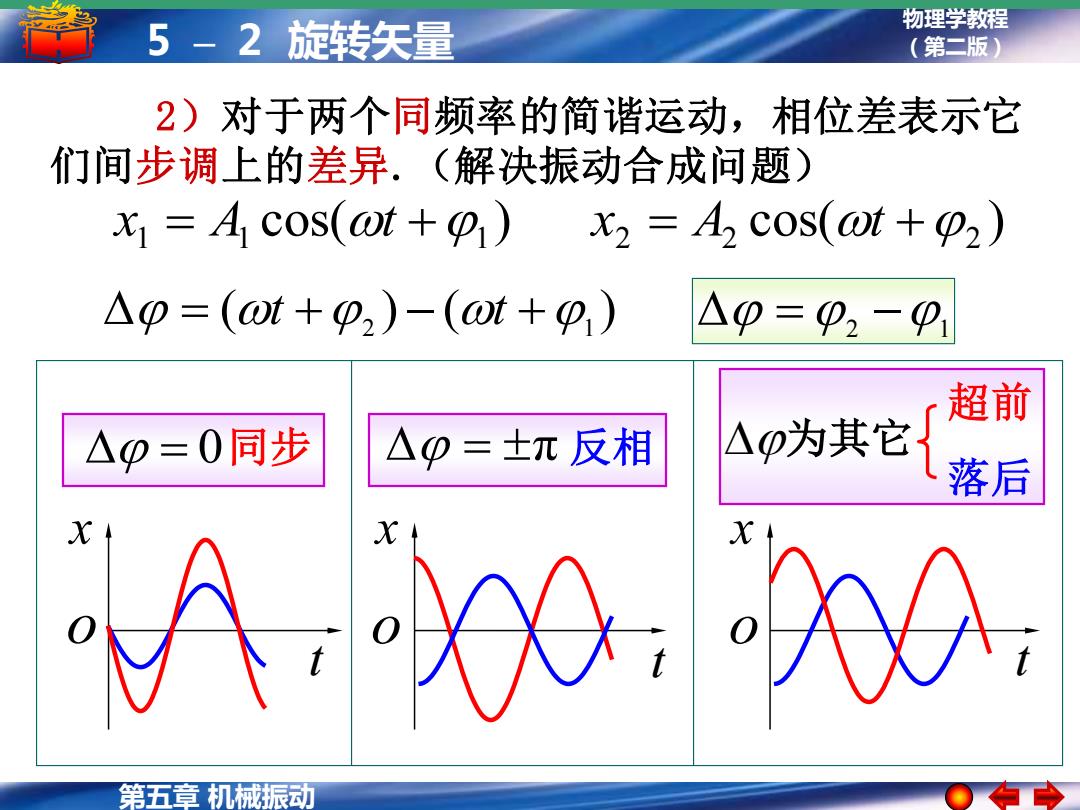
5-2旋转矢量 物理学教程 (第二版) 2)对于两个同频率的简谐运动,相位差表示它 们间步调上的差异.(解决振动合成问题) x=A cos(ot+) x2=A cos(@t+2) △p=(ot+p2)-(0t+p,) △0=p2-p1 超前 △0=0同步 △0=士元反相 △p为其它 落后 0:e 第五章机械振动
物理学教程 5 – 2 旋转矢量 (第二版) 第五章 机械振动 = 0 x t o 同步 2)对于两个同频率的简谐运动,相位差表示它 们间步调上的差异.(解决振动合成问题) cos( ) 1 = 1 +1 x A t cos( ) 2 = 2 +2 x A t ( ) ( ) = + 2 − +1 t t = 2 −1 x t o 为其它 超前 落后 t x o = π 反相

5-2旋转矢量 物理学教程 (第二版) 例1如图所示,一轻弹簧的右端连着一物体,弹 簧的劲度系数k=0.72Nm,物体的质量m=20g. (1)把物体从平衡位置向右拉到X=0.05m处停 下后再释放,求简谐运动方程; A (2)求物体从初位置运动到第一次经过二处时的 速度; 2 (3)如果物体在x=0.05m处时速度不等于零, 而是具有向右的初速度v,=0.30m·s,求其运动方程. x/m 00.05 第五章机械振动
物理学教程 5 – 2 旋转矢量 (第二版) 第五章 机械振动 例1 如图所示,一轻弹簧的右端连着一物体,弹 簧的劲度系数 ,物体的质量 . (1)把物体从平衡位置向右拉到 处停 下后再释放,求简谐运动方程; 1 0.72N m − k = m = 20g x = 0.05m x = 0.05m 1 0 0.30m s − v = (3)如果物体在 处时速度不等于零, 而是具有向右的初速度 ,求其运动方程. 2 A (2)求物体从初位置运动到第一次经过 处时的 速度; x / m o 0.05

5-2旋转矢量 物理学教程 (第二版) 0.72N.m- 解 (1) 0= 6.0s = m 0.02kg =+ =x,=0.05m tan⑩= =0=0 0X0 A X p=0或元 由旋转矢量图可知0=0 x=Acos(at+o)=0.05cos6.0t m 第石章机械振动
物理学教程 5 – 2 旋转矢量 (第二版) 第五章 机械振动 o x 解 (1) 1 1 6.0s 0.02kg 0.72N m − − = = = m k 2 0 0.05m 2 2 0 A = x0 + = x = v tan 0 0 0 = − = x v = 0 或 π A 由旋转矢量图可知 = 0 x = Acos(t +)= 0.05cos6.0t m