
7-1平衡态理想气体物态方程热力学第零定律 物理学教程 (第二版) 热学涉及到宏观与微观两个层次 宏观理论热力学的两大基本定律:第一定律,即 能量守恒定律;第二定律,即熵增加定律. 科学家进一步追根问底,企图从分子和原子的微 观层次上来说明物理规律,气体分子动理论应运而生. 玻尔兹曼与吉布斯发展了经典统计力学. 热力学与统计物理的发展,加强了物理学与化学 的联系,建立了物理化学这一门交叉科学. 第七章气体动理论
第七章 气体动理论 物理学教程 7-1 平衡态 理想气体物态方程 热力学第零定律 (第二版) 热学涉及到宏观与微观两个层次 热力学与统计物理的发展, 加强了物理学与化学 的联系, 建立了物理化学这一门交叉科学. 宏观理论热力学的两大基本定律: 第一定律, 即 能量守恒定律; 第二定律, 即熵增加定律 . 玻尔兹曼与吉布斯发展了经典统计力学 . 科学家进一步追根问底, 企图从分子和原子的微 观层次上来说明物理规律, 气体分子动理论应运而生

7-1平衡态理想气体物态方程热力学第零定律 物理学教程 (第二版) 研究对象 热现象:与温度有关的物理性质的变化。 热运动:构成宏观物体的大量微观粒子的永不 休止的无规运动. 研究对象特征 单个分子一无序、具有偶然性、遵循力学规律: 整体(大量分子)一服从统计规律. 微观量:描述个别分子运动状态的物理量(不可 直接测量),如分子的m,)等. 宏观量:表示大量分子集体特征的物理量(可直 接测量),如p,V,T等. 第七章气体动理论
第七章 气体动理论 物理学教程 7-1 平衡态 理想气体物态方程 热力学第零定律 (第二版) ➢ 研究对象 热运动 : 构成宏观物体的大量微观粒子的永不 休止的无规运动 . 热现象 : 与温度有关的物理性质的变化。 单个分子 — 无序、具有偶然性、遵循力学规律. ➢ 研究对象特征 整体(大量分子)— 服从统计规律 . 宏观量:表示大量分子集体特征的物理量(可直 接测量), 如 p,V,T 等 . 微观量:描述个别分子运动状态的物理量(不可 直接测量),如分子的 v 等 . m

7·1平衡态理想气体物态方程热力学第零定律 物理学教程 (第二版) 微观量 统计平均 宏观量 研究方法 1.热力学 宏观描述 实验经验总结,给出宏观物体热现象的规律, 从能量观点出发,分析研究物态变化过程中热功转 换的关系和条件. 2.气体动理论— 微观描述 研究大量数目的热运动的粒子系统,应用模型 假设和统计方法揭示宏观现象的本质 热力学 相辅相成 气体动理论 第七章气体动理论
第七章 气体动理论 物理学教程 7-1 平衡态 理想气体物态方程 热力学第零定律 (第二版) 微观量 统计平均 宏观量 ➢ 研究方法 1. 热力学 —— 宏观描述 实验经验总结, 给出宏观物体热现象的规律, 从能量观点出发,分析研究物态变化过程中热功转 换的关系和条件 . 2. 气体动理论 —— 微观描述 研究大量数目的热运动的粒子系统,应用模型 假设和统计方法揭示宏观现象的本质 . 热力学 相辅相成 气体动理论

7-1平衡态理想气体物态方程热力学第零定律 物理学教程 (第二版) 气体的物态参量(宏观量) 1气体压强卫:作用于容器壁上 单位面积的正压力(力学描述), 单位: 1Pa =1N.m-2 标准大气压:45°纬度海平面处,0C时的大气压. 1atm=1.013×103Pa 2体积V:气体所能达到的最大空间(几何 描述 单位:1m3=103L=103dm3 3温度T:气体冷热程度的量度(热学描述) 单位:温标K(开尔文).T=273.15+t 第七章气体动理论
第七章 气体动理论 物理学教程 7-1 平衡态 理想气体物态方程 热力学第零定律 (第二版) 一 气体的物态参量(宏观量) p,V,T 1 气体压强 :作用于容器壁上 单位面积的正压力(力学描述). p 单位: 2 1Pa 1N m − = 2 体积 : 气体所能达到的最大空间(几何 描述). 3 3 3 3 1m =10 L =10 dm V 单位: 1atm 1.013 10 Pa 5 = 标准大气压: 纬度海平面处, 时的大气压. 45 0 C 3 温度 T : 气体冷热程度的量度(热学描述). 单位:温标 K(开尔文). T = 273.15 + t

7-1平衡态理想气体物态方程热力学第零定律 物理学教程 (第二版) 二平衡态 一定量的气体,在不受外界的影响下,经过 一定的时间,系统达到一个稳定的,宏观性质不随 时间变化的状态称为平衡态.(理想状态) 真空膨胀 p.V.T ·(p,V,T) 自发 (p',V',T) p',/',T 第七章气体动理论
第七章 气体动理论 物理学教程 7-1 平衡态 理想气体物态方程 热力学第零定律 (第二版) p,V,T 真 空 膨 胀 p o V p ,V ,T 二 平 衡 态 一定量的气体,在不受外界的影响下, 经过 一定的时间, 系统达到一个稳定的, 宏观性质不随 时间变化的状态称为平衡态 .(理想状态) ( p,V,T) ( p ,V ,T) 自发

7-1平衡态理想气体物态方程热力学第零定律 物理学教程 (第二版) 平衡态的特点 p-V图 *(p,V,T) 上的每一点 (p,',T) 表示一个平 衡态 1)单一性(D,T处处相等); 2)物态的稳定性一 与时间无关; 3)自发过程的终点; 4)热动平衡(有别于力平衡). 第七章气体动理论
第七章 气体动理论 物理学教程 7-1 平衡态 理想气体物态方程 热力学第零定律 (第二版) 平衡态的特点 1)单一性( 处处相等); 2)物态的稳定性—— 与时间无关; 3)自发过程的终点; 4)热动平衡(有别于力平衡). p,T ( p,V,T) p V * ( p,V,T) o p -V 图 上的每一点 表示一个平 衡态

7-1平衡态理想气体物态方程热力学第零定律 物理学教程 (第二版) 三 理想气体物态方程 理想气体宏观定义:遵守三个实验定律的气体. 物态方程:理想气体平衡态宏观参量间的函数 关系 PV-NkT k=1.38×10-23J.K-1 令 V=N/NA 阿伏伽德罗常数 则 pV=vNkT N =6.02x1023mol-1 令NAk=R 则 DV-VRI 第七音气体动理论
第七章 气体动理论 物理学教程 7-1 平衡态 理想气体物态方程 热力学第零定律 (第二版) 三 理想气体物态方程 物态方程:理想气体平衡态宏观参量间的函数 关系 . pV = NkT 理想气体宏观定义:遵守三个实验定律的气体 . 2 3 1 1.38 10 J K − − k = 令 = N NA 则 pV =NA kT 令 NA k = R 则 pV =RT23 1 A 6.02 10 mol − N = 阿伏伽德罗常数

7-1平衡态理想气体物态方程热力学第零定律 物理学教程 (第二版) PV=VRT V=NNA 对质量为m'的理想气体v=m'/M 理想气体 物态方程 pV= 摩尔气体常量R=8.31Jmol1.K-1 分子数密度(几):单位体积内的分子数目. n=N/V p =nkT 第七章气体动理论
第七章 气体动理论 物理学教程 7-1 平衡态 理想气体物态方程 热力学第零定律 (第二版) 1 1 8.31J mol K − − 摩尔气体常量 R = RT M m pV ' = 理想气体 物态方程 对质量为 m' 的理想气体 = m' M pV =RT = N NA n = N V p = nkT 分子数密度( n ):单位体积内的分子数目
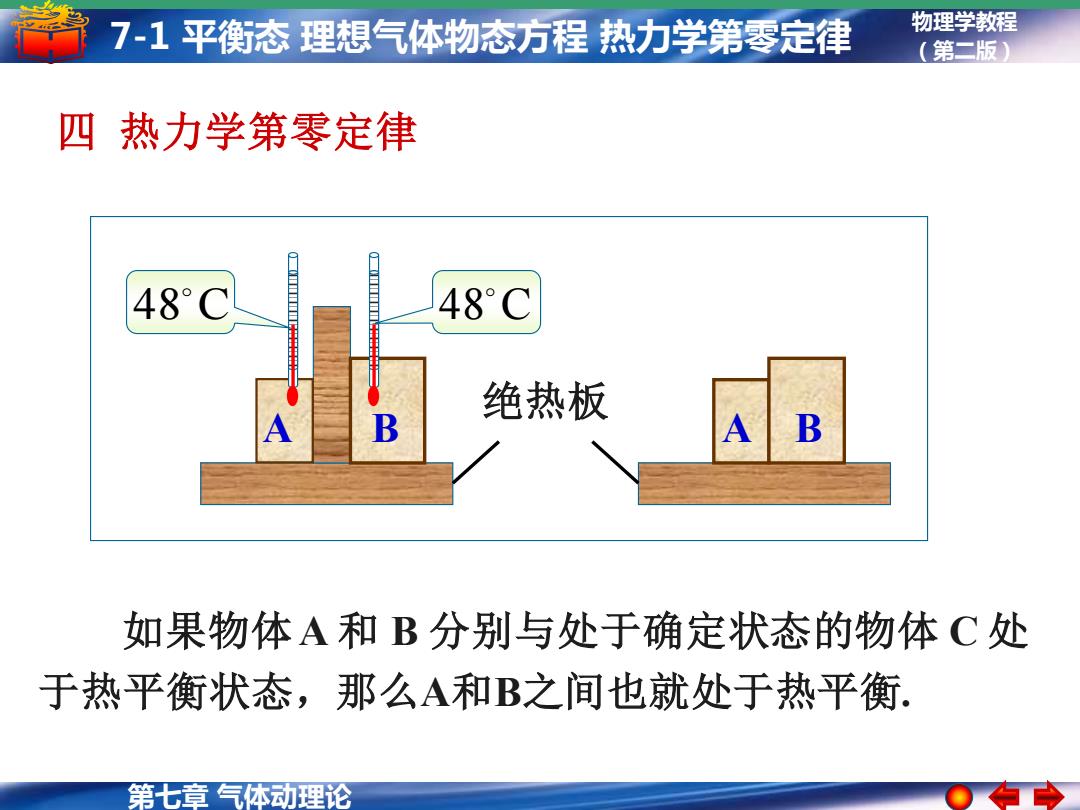
7-1平衡态理想气体物态方程热力学第零定律 物理学教程 (第二版) 四热力学第零定律 48°( 48°C 绝热板 B 如果物体A和B分别与处于确定状态的物体C处 于热平衡状态,那么A和B之间也就处于热平衡. 第七章气体动理论
第七章 气体动理论 物理学教程 7-1 平衡态 理想气体物态方程 热力学第零定律 (第二版) 四 热力学第零定律 如果物体A 和 B 分别与处于确定状态的物体 C 处 于热平衡状态,那么A和B之间也就处于热平衡. 绝热板 A B A B 48 C 48 C