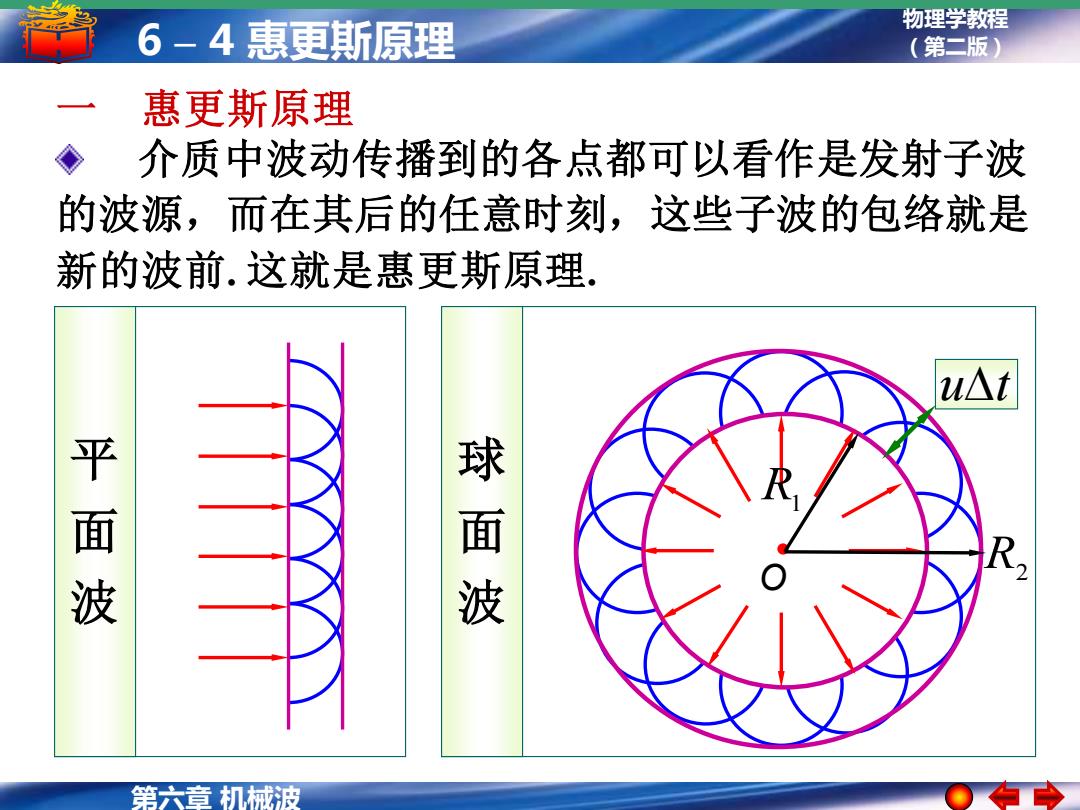
物理学教程 6-4惠更斯原理 (第二版) 惠更斯原理 ◆ 介质中波动传播到的各点都可以看作是发射子波 的波源,而在其后的任意时刻,这些子波的包络就是 新的波前.这就是惠更斯原理, u△t 平面波 球面波 第六音机械被
物理学教程 (第二版) 第六章 机械波 6 – 4 惠更斯原理 球 面 波 平 面 波 介质中波动传播到的各点都可以看作是发射子波 的波源,而在其后的任意时刻,这些子波的包络就是 新的波前. 这就是惠更斯原理. 一 惠更斯原理 O R1 R2 ut

6-4惠更斯原理 物理学教程 (第二版) 波的衍射 波在传播过程中遇到障碍物时,能绕过障碍物 的边缘,在障碍物的阴影区内继续传播。 波的行射 水波通过狭缝后的衍射 第六章机械波
物理学教程 (第二版) 第六章 机械波 6 – 4 惠更斯原理 波 的 衍 射 水 波 通 过 狭 缝 后 的 衍 射 波在传播过程中遇到障碍物时,能绕过障碍物 的边缘,在障碍物的阴影区内继续传播. 波的衍射

物理学教程 6-4惠更斯原理 (第二版) 二 波的干涉 1 波的叠加原理 日 几列波相遇之后,仍然保持它们各自原有的特征 (频率、波长、振幅、振动方向等)不变,并按照原来 的方向继续前进,好象没有遇到过其他波一样.(独立性) 日 在相遇区域内任一点的振动,为各列波单独存在 时在该点所引起的振动位移的矢量和.(叠加性) 第六音机械波
物理学教程 (第二版) 第六章 机械波 6 – 4 惠更斯原理 二 波的干涉 几列波相遇之后,仍然保持它们各自原有的特征 (频率、波长、振幅、振动方向等)不变, 并按照原来 的方向继续前进, 好象没有遇到过其他波一样.(独立性) 在相遇区域内任一点的振动,为各列波单独存在 时在该点所引起的振动位移的矢量和.(叠加性) 1 波的叠加原理

6-4惠更斯原理 物理学教程 (第二版) 2波的干涉 频率相同、 振动方向平行、 相位相同或相位 差恒定的两列波 相遇时,使某些 源 地方振动始终加 强,而使另一些 地方振动始终减 弱的现象,称为 波的干涉现象。 第六章机械波
物理学教程 (第二版) 第六章 机械波 6 – 4 惠更斯原理 频率相同、 振动方向平行、 相位相同或相位 差恒定的两列波 相遇时,使某些 地方振动始终加 强,而使另一些 地方振动始终减 弱的现象,称为 波的干涉现象. 2 波的干涉

6-4惠更斯原理 物理学教程 (第二版) 水波的干涉现象 第六音机械波
物理学教程 (第二版) 第六章 机械波 6 – 4 惠更斯原理 水 波 的 干 涉 现 象

物理学教程 6-4惠更斯原理 (第二版) >波的相干条件 1)频率相同; 2)振动方向平行; 3)相位相同或相位差恒定. y1=Ac0s(ot+p)) 波源振动 y2=A2 cos(ot+2) ryp=Acos(ot+m-2π 点P的两个分振动 y2p=A,2c0s(0t+p2-2π 第六章机械波
物理学教程 (第二版) 第六章 机械波 6 – 4 惠更斯原理 1 s 2 s P * 1 r 2 r 波源振动 cos( ) 1 = 1 +1 y A t cos( ) 2 = 2 +2 y A t cos( 2π ) 1 1 1 1 r y A t p = + − cos( 2π ) 2 2 2 2 r y A t p = + − 点P 的两个分振动 1)频率相同; 2)振动方向平行; 3)相位相同或相位差恒定. ➢ 波的相干条件

物理学教程 6-4惠更斯原理 (第二版) 点P的两个分振动 r hp=Ac0s(ot+0,-2π y2p=A,c0s(0t+p2-2元 yp=yip+y2p Acos(ot+p) 22) sin()sin(z tano 2ri)+4cos(p2-元 4cos(01- 4=2+2+244 cosAp △0=0,-0,-2元2-1 常量 第六音机械波
物理学教程 (第二版) 第六章 机械波 6 – 4 惠更斯原理 cos( ) y p = y1 p + y2 p = A t + ) 2π ) cos( 2π cos( ) 2π ) sin( 2π sin( tan 1 2 2 1 1 1 2 2 2 1 1 1 r A r A r A r A − + − − + − = = + + 2 1 2 cos 2 2 2 A A1 A A A 1 s 2 s P * 1 r 2 r cos( 2π ) 1 1 1 1 r y A t p = + − cos( 2π ) 2 2 2 2 r y A t p = + − 点P 的两个分振动 2 1 2 1 2π r − r = − − 常量

物理学教程 6-4惠更斯原理 (第二版) A=VA4+A+2AA,c0s△0 讨论 A0=p2-0,-2r 2-7 1) 合振动的振幅(波的强度)在空间各点的分 布随位置而变,但是稳定的, △p=±2k元k=0,1,2,. A=4+4 振动始终加强 2)〈 △0=±(2k+1)元k=0,1,2,… A=4-4 振动始终减弱 △p=其他A-A <A<A,+A, 第六章机械波
物理学教程 (第二版) 第六章 机械波 6 – 4 惠更斯原理 讨 论 1 ) 合振动的振幅(波的强度)在空间各点的分 布随位置而变,但是稳定的. = 2k π k = 0,1,2, = (2k +1)π k = 0,1,2, A1 − A2 A A1 + A2 = 其他 A = A1 + A2 振动始终加强 A = A1 − A2 振动始终减弱 2 ) = + + 2 1 2 cos 2 2 2 A A1 A A A 2 1 2 1 2π r − r = − −

物理学教程 6-4惠更斯原理 (第二版) 「A=VA+号+2AA,cos△0 讨论 A0=p2-0,-2元2 2 若P1=P2则△0=-2π 波程差6=?-片 δ=±k几k= 0,1,2,… 4=4+4 振动始终加强 3) δ=±(k+1/2)入 k=0,1,2,. A=4-4 振动始终减弱 6=其他 A-A<A<A+A 第六音机械波
物理学教程 (第二版) 第六章 机械波 6 – 4 惠更斯原理 波程差 2 1 若 1 = 2 则 = r − r = −2π A = A1 − A2 振动始终减弱 A = A1 + A2 振动始终加强 = (k +1 2) k = 0,1,2, = 其他 A1 − A2 A A1 + A2 = k k = 0,1,2, 3 ) 讨 论 = + + 2 1 2 cos 2 2 2 A A1 A A A 2 1 2 1 2π r − r = − −

6-4惠更斯原理 物理学教程 (第二版) 例如图所示,A、B两点为同一介质中两相干波 源.其振幅皆为5cm,频率皆为100Hz,但当点A为波 峰时,点B恰为波谷.设波速为l0m/s,试写出由A、B 发出的两列波传到点P时干涉的结果 T 解BP=V152+202m=25m 15m u10 = m=0.10m 100 B 20m- 设A的相位较B超 前,则p4-9B=元 BP-AP 25-15 △0=0B-p4-2元 =-元-2元 =-201元 入 0.1 点P合振幅 A=A-A2=0 第六章机械波
物理学教程 (第二版) 第六章 机械波 6 – 4 惠更斯原理 例 如图所示,A、B 两点为同一介质中两相干波 源.其振幅皆为5cm,频率皆为100Hz,但当点 A 为波 峰时,点B 恰为波谷.设波速为10m/s,试写出由A、B 发出的两列波传到点P 时干涉的结果. 解 15m 20m A B P 15 20 m 25 m 2 2 BP = + = m 0.10 m 100 10 = = = u 设 A 的相位较 B 超 前,则 − =π . A B 201π 0.1 25 15 2π π 2π = − − = − − − = − − BP AP B A 点P 合振幅 A = A1 − A2 = 0