
6-2平面简谐波的波函数 物理学教程 (第二版) 平面简谐波的波函数 介质中任一质点(坐标为x)相对其平衡位置的 位移(坐标为y)随时间的变化关系,即y(x,)称 为波函数。 y=y(x,t) 各质点相对平 波线上各质点 衡位置的位移 平衡位置 > 简谐波:在均匀的、无吸收的介质中,氵 波源作 简谐运动时,在介质中所形成的波. 平面简谐波:波面为平面的简谐波, 第六章机械波
物理学教程 (第二版) 第六章 机械波 6 – 2 平面简谐波的波函数 y = y(x,t) 各质点相对平 衡位置的位移 波线上各质点 平衡位置 ➢ 简谐波:在均匀的、无吸收的介质中,波源作 简谐运动时,在介质中所形成的波. 一 平面简谐波的波函数 ➢ 平面简谐波:波面为平面的简谐波. 介质中任一质点(坐标为 x)相对其平衡位置的 位移(坐标为 y)随时间的变化关系,即 称 为波函数. y(x,t)
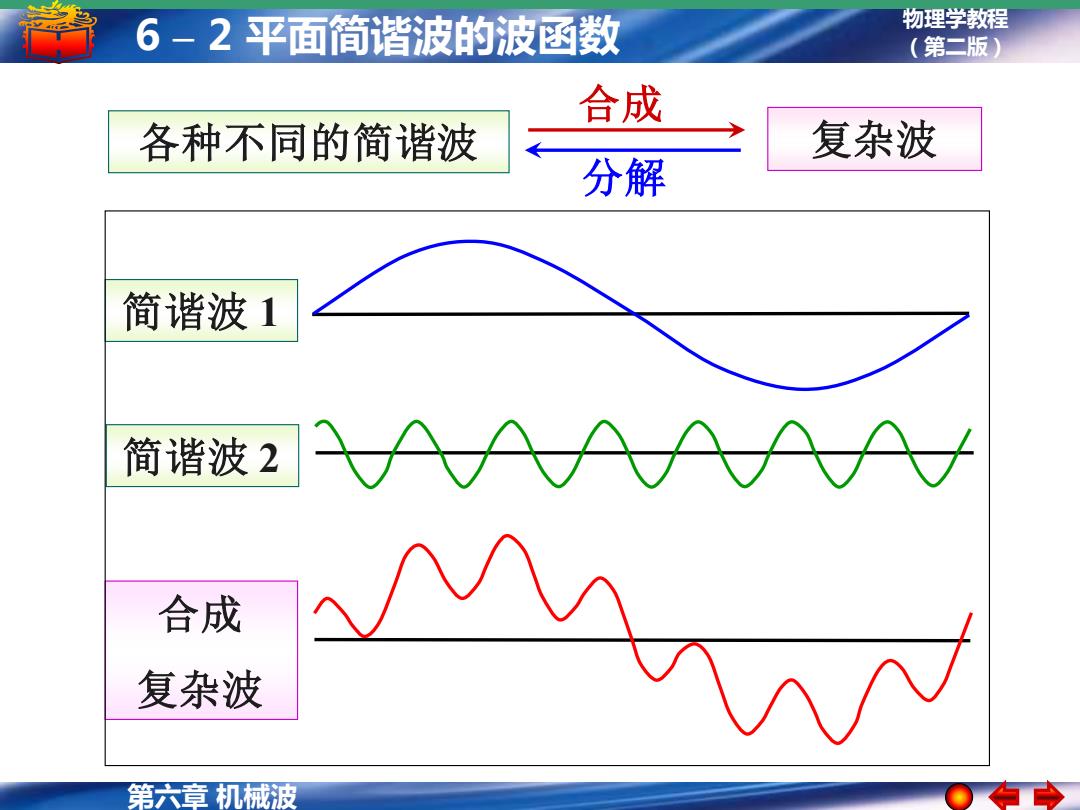
6-2平面简谐波的波函数 物理学教程 (第二版) 合成 各种不同的简谐波 复杂波 分解 简谐波1 简谐波2 合成 复杂波 第六章机械波
物理学教程 (第二版) 第六章 机械波 6 – 2 平面简谐波的波函数 简谐波 1 简谐波 2 合成 复杂波 各种不同的简谐波 复杂波 合成 分解
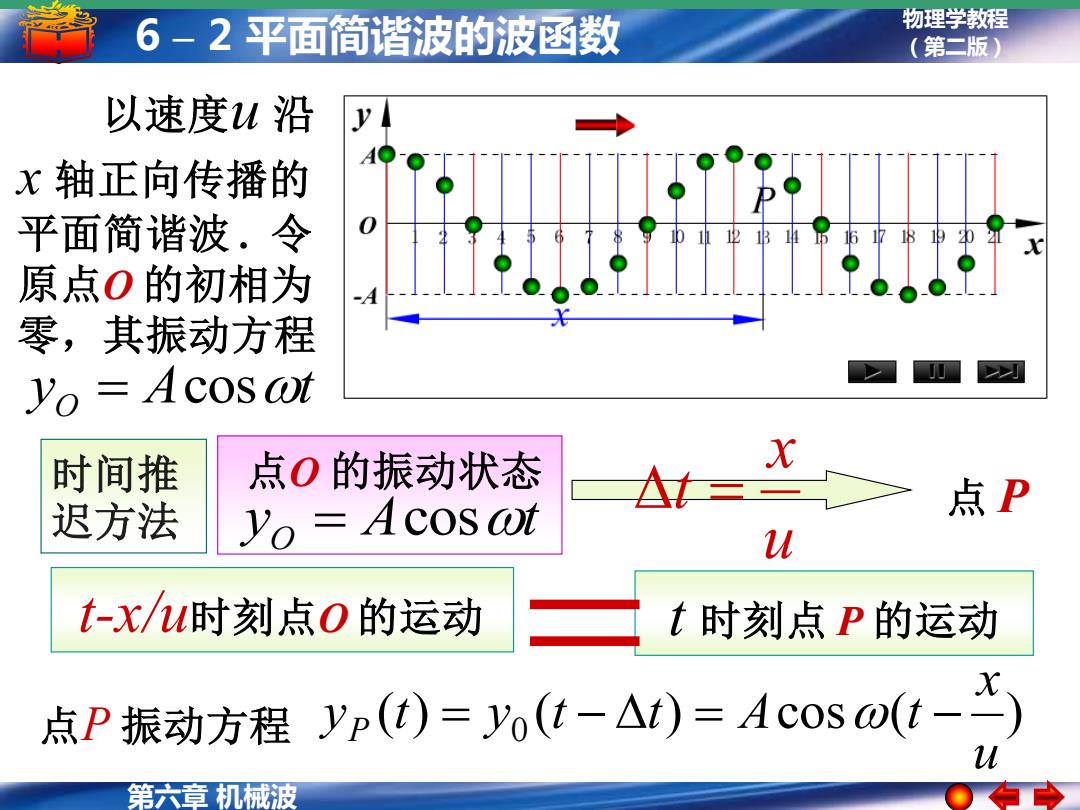
6-2平面简谐波的波函数 物理学教程 (第二版) 以速度u沿 x轴正向传播的 平面简谐波.令 1 原点0的初相为 零,其振动方程 Yo Acos@t 时间推 点O的振动状态 △= X 迟方法 Yo =Acos ot 点P u t-X/u时刻点O的运动 t时刻点P的运动 点P振动方程yp(t)=y(t-△)=Acosofi-X) 第六章机械波
物理学教程 (第二版) 第六章 机械波 6 – 2 平面简谐波的波函数 点O 的振动状态 y A t O = cos 点 P u x t = t-x/u时刻点O 的运动 t 时刻点 P 的运动 以速度u 沿 x 轴正向传播的 平面简谐波 . 令 原点O 的初相为 零,其振动方程 y A t O = cos ( ) =( ) cos ( ) 0 u x y t y t t A t 点P 振动方程 P = − = − 时间推 迟方法

6-2平面简谐波的波函数 物理学教程 (第二版) 波函数 y=Acos@(t-) u 相位落后法 点O振动方程 y。=Acos wt x=0,p=0 X 点P比点O落后的相位△0=9,-p0=-2π X 0p=-2π=-2元 X Tu u 点P振动方程 yp=Acoso(t- 第六章机械波
物理学教程 (第二版) 第六章 机械波 6 – 2 平面简谐波的波函数 点 P 比点 O 落后的相位 = p − O x = −2π u x Tu x x p = −2π = −2π = − cos ( ) u x y A t 点 P 振动方程 p = − y A t o = cos 点 O 振动方程 x = 0, = 0 ➢ 波函数 cos ( ) u x y = A t − P x * y x u A − A O 相位落后法

6-2平面简谐波的波函数 物理学教程 (第二版) 如果原点的 初相位不为零 x=0,0≠0 点O振动方程 yo Acos(ot +p) 波 y=Ac0sot-式+p]u沿x轴正向 函 数 y=Acos[o(t日)+p]u沿x轴负向 第六章机械波
物理学教程 (第二版) 第六章 机械波 6 – 2 平面简谐波的波函数 x = 0, 0 = cos[( + ) +] u x y A t u 沿 x 轴负向 y = Acos(t +) 点 O 振动方程 O 波 函 数 = cos[( − ) +] u 沿 x 轴正向 u x y A t y x u A − A O 如果原点的 初相位不为零

6-2平面简谐波的波函数 物理学教程 (第二版) 平面简谐波波函数的其它形式 0x)-Aco2x-为+ y(x,t)=Acos(a) >质点的振动速度,加速度 角波数k=2π 0 =-@Asin[o(t-X)+o] Ot a= oAcosto(t 812 第六章机械波
物理学教程 (第二版) 第六章 机械波 6 – 2 平面简谐波的波函数 ➢ 平面简谐波波函数的其它形式 ( ) = cos[2 π( − ) +] λ x T t y x,t A y(x,t) = Acos(t − kx +) 2π ➢ 质点的振动速度,加速度 角波数 k = = − sin[( − ) +] = u x A t t y v cos[ ( ) ] 2 2 2 = − − + = u x A t t y a

6-2平面简谐波的波函数 物理学教程 (第二版) 讨论 1)给出下列波函数所表示的波的传播方向 和x=0点的初相位, ,(向x轴正向传播, y=-Acosw(-t-)(向x轴负向传播,p=π) 2)平面简谐波的波函数为y=Acos(Bt-Cx) 式中A,B,C为正常数,求波长、波速、波传播方 向上相距为d的两点间的相位差 y=Acos(Bt-Cx) 42号 2元 2元 T B d △0=2π B 第六章机械波
物理学教程 (第二版) 第六章 机械波 6 – 2 平面简谐波的波函数 1)给出下列波函数所表示的波的传播方向 和 x = 0 点的初相位. cos 2π ( ) x T t y = −A − cos ( ) u x y = −A −t − 2)平面简谐波的波函数为 式中 为正常数,求波长、波速、波传播方 向上相距为 的两点间的相位差. y = Acos(Bt −Cx) A,B,C d y = Acos(Bt −Cx) cos 2 π ( ) x T t y = A − C 2π = B T 2π = C B T u = = dC d = = 2π 讨 论 ( 向x 轴正向传播 , =π ) ( 向x 轴负向传播 , =π )

6-2平面简谐波的波函数 物理学教程 (第二版) 二 波函数的物理意义 y=cos-+=Acos2m号为+pl 1当X固定时,波函数表示该点的简谐运动 方程,并给出该点与点O振动的相位差 △0=-wx=-2π9 y(x,t)=y(x,t+T)(波具有时间的周期性) 第六章机械被
物理学教程 (第二版) 第六章 机械波 6 – 2 平面简谐波的波函数 二 波函数的物理意义 cos[ ( ) ] cos[2 π( ) ] = − + = − + x T t A u x y A t 1 当 x 固定时, 波函数表示该点的简谐运动 方程,并给出该点与点 O 振动的相位差. λ x u x = − = −2 π y(x,t) = y(x,t +T) (波具有时间的周期性)
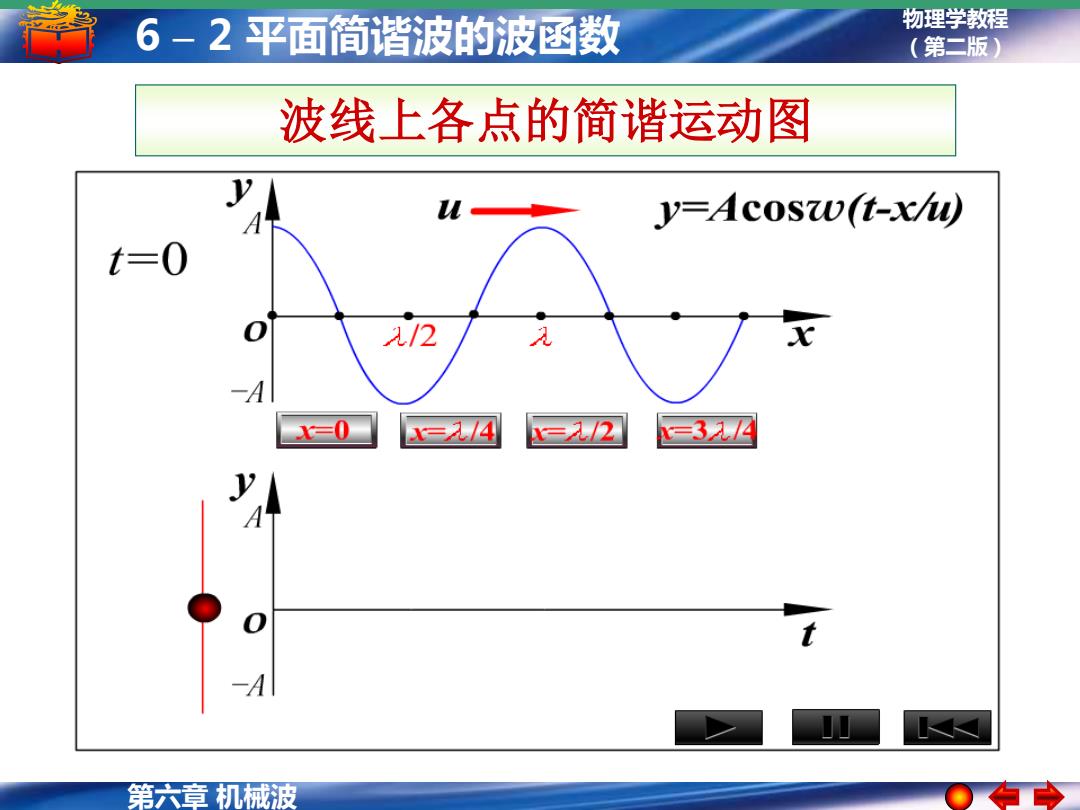
6-2平面简谐波的波函数 物理学教程 (第二版) 波线上各点的简谐运动图 y=Acosw(t-xu) t=0 /2 3=0 =2/4 =2/2 =3元☑ 第六章机械波
物理学教程 (第二版) 第六章 机械波 6 – 2 平面简谐波的波函数 波线上各点的简谐运动图

6-2平面简谐波的波函数 物理学教程 (第二版) cocos[2+ 1 2当一定时,波函数表示该时刻波线上各点 相对其平衡位置的位移,即此刻的波形 yco2 y(x,t)=y(x+几,t)(波具有空间的周期性) 波程差 Ax21=X2-1 △012=01-02=2π -x=2π X21 △x △0=2元 第六章机械波
物理学教程 (第二版) 第六章 机械波 6 – 2 平面简谐波的波函数 2 当 一定时,波函数表示该时刻波线上各点 相对其平衡位置的位移,即此刻的波形. t cos[ ( ) ] cos[2 π( ) ] = − + = − + x T t A u x y A t y(x,t) = y(x + ,t) (波具有空间的周期性) cos[ 2 π (2π )] = − + + T x t y A 2 1 2 1 1 2 1 2 2π 2π x x x = − = − = 波程差 21 2 1 x = x − x x = 2π