4-4力矩作功刚体绕定轴转动的动能定 物理学教程 (第二版) 力的空间累积效应二>力的功,动能,动能定理. 力矩的空间累积效应力矩的功,转动动能,动能定理 力矩作功 dw=F.dr=Fds do Frd0 dw=Mde 力矩的功 Mdo 二 力矩的功率 P dw do =M = Mo dt dt 第四章刚休转动
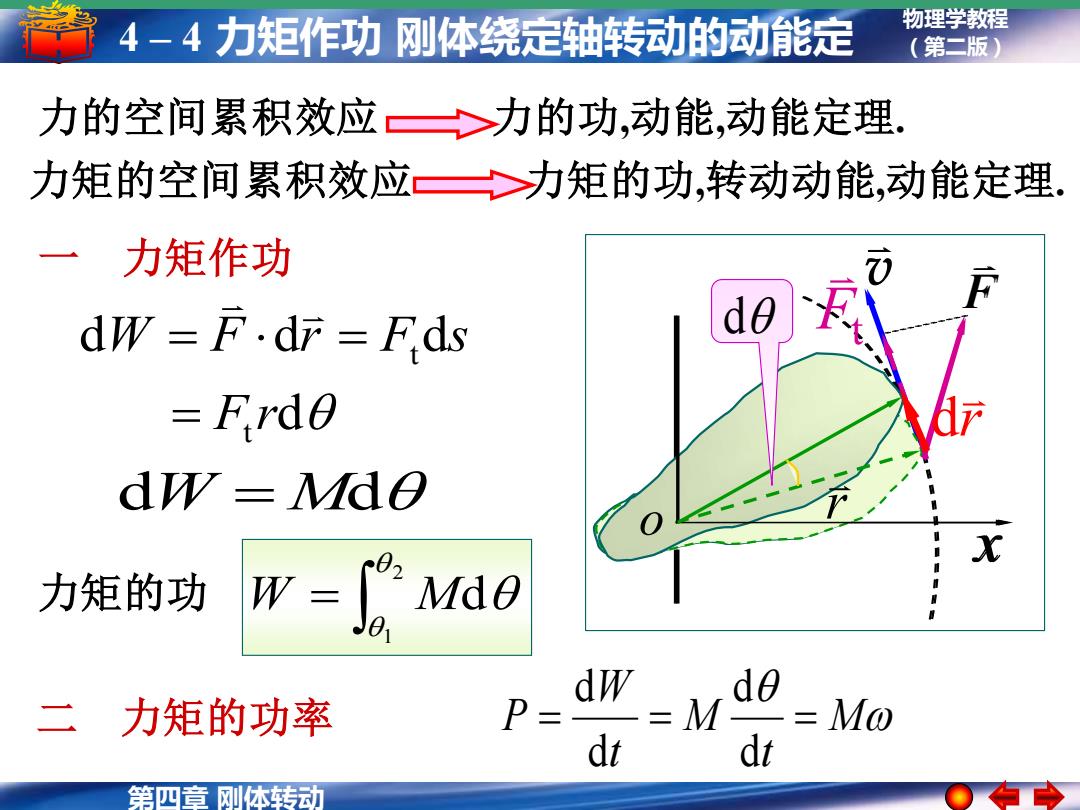
第四章 刚体转动 物理学教程 4 – 4 力矩作功 刚体绕定轴转动的动能定 (第二版) 理 d d d d t t F r W F r F s = = = dW = Md = 2 1 d 力矩的功 W M 一 力矩作功 力的空间累积效应 力的功,动能,动能定理. 力矩的空间累积效应 力矩的功,转动动能,动能定理. M t M t W P = = = d d d d 二 力矩的功率 o r v F x v F o x r Ft r d d

4-4力矩作功刚体绕定轴转动的动能定 物理学教程 (第二版) 三 转动动能 A-∑am或-区nuwo 四 刚体绕定轴转动的动能定理 w-8=gJ0=广oa E=a0=2o2® 合外力矩对绕定轴转动的刚体所作的功等于刚体 转动动能的增量. 第四章刚体转动
第四章 刚体转动 物理学教程 4 – 4 力矩作功 刚体绕定轴转动的动能定 (第二版) 理 2 1 2 2 2 1 2 1 d 2 1 W = M = J − J 三 转动动能 2 2 1 i i i Ek = m v 四 刚体绕定轴转动的动能定理 = 2 1 d W M 合外力矩对绕定轴转动的刚体所作的功等于刚体 转动动能的增量 . 2 2 2 2 1 ( ) 2 1 mi ri J i = = = = 2 1 1 1 d d d d J t J
4-4力矩作功刚体绕定轴转动的动能定 物理学教程 (第二版) 质点运动与刚体定轴转动对照 质点运动 刚体定轴转动 dr = do 速度 角速度 dt dt 加速度 d do a= 角加速度 Q= dt dt 力 疗 力矩 M 质量 m 转动惯量 J-「r2dm 动量 P =mi 角动量 i=Jò 第四章刚体转动
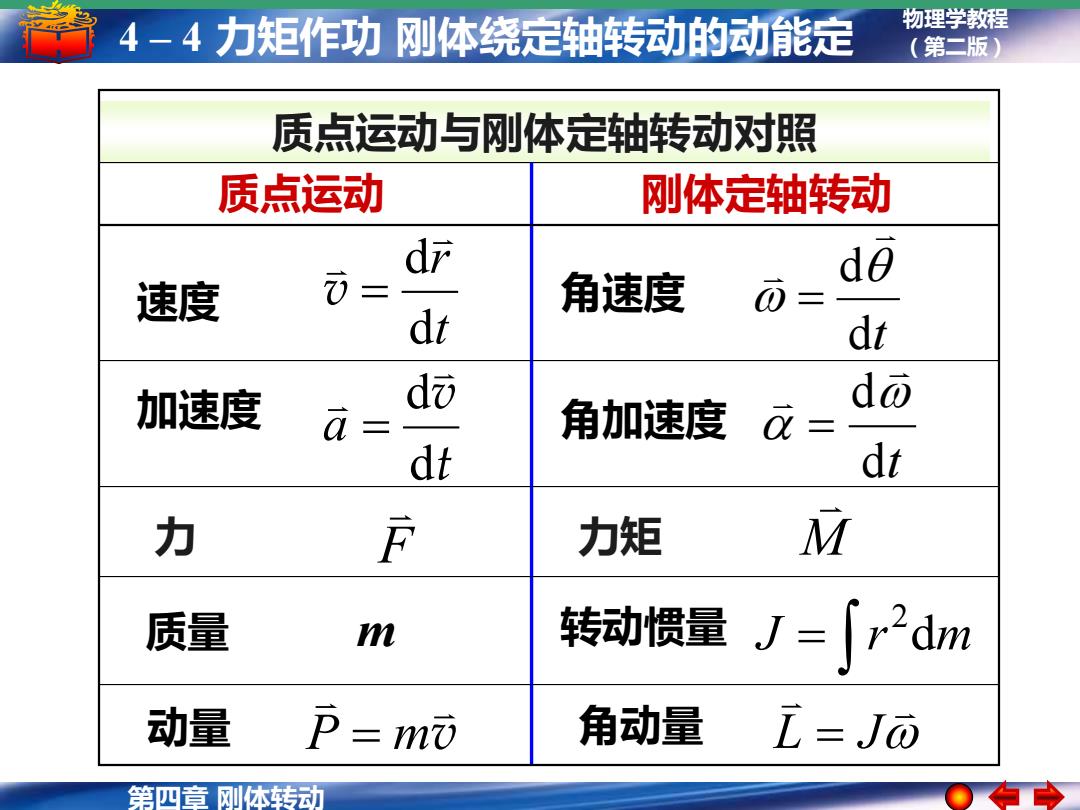
第四章 刚体转动 物理学教程 4 – 4 力矩作功 刚体绕定轴转动的动能定 (第二版) 理 质点运动与刚体定轴转动对照 质点运动 刚体定轴转动 速度 加速度 t r d d v = t v d d a = 角速度 角加速度 dt d = dt d = 质量 m 转动惯量 动量 角动量 J r dm 2 = v L = J P = m 力 F 力矩 M

4一4力矩作功刚体绕定轴转动的动能定 物理学教程 (第二版) 质点运动规律与刚体定轴转动的规律对照 质点的平动 刚体的定轴转动 运动定律 F=ma 转动定律 M=Ja 动量定理 角动量定理 =m0 -m0 Adr--to 动量守恒定律 角动量守恒定律 ∑万=0,∑m可,=恒量 M=0,∑J,o,=恒量 力的功 w-fF.dr 力矩的功, =6 动能 Ek=mo2/2 转动动能 Ex=Jo2/2 第四章刚体转动
第四章 刚体转动 物理学教程 4 – 4 力矩作功 刚体绕定轴转动的动能定 (第二版) 理质点运动规律与刚体定轴转动的规律对照 运动定律 F ma = 转动定律 M = J 质点的平动 刚体的定轴转动 动量定理 0 0 d v v F t m m t t = − 角动量定理 0 0 Mdt L L t t = − 动量守恒定律 角动量守恒定律 Fi = mi vi = 恒量 0, M = Ji i = 恒量 0, 力的功 = b a W F r d 力矩的功 = 0 W Md 动能 / 2 2 Ek = mv 转动动能 / 2 2 Ek = J

4-4力矩作功刚体绕定轴转动的动能定 物理学教程 (第二版) 质点运动规律与刚体定轴转动的规律对照 质点的平动 刚体的定轴转动 动能定理 动能定理 W三 1 mo2 W= 2 2 Jo2 2 2 重力势能 Ep =mgh 重力势能 Ep =mghc 机械能守恒 机械能守恒 只有保守力作功时 只有保守力作功时 Ek+E,=恒量 Ek+E。=恒量 第四章刚体转动
第四章 刚体转动 物理学教程 4 – 4 力矩作功 刚体绕定轴转动的动能定 (第二版) 理 质点运动规律与刚体定轴转动的规律对照 质点的平动 刚体的定轴转动 动能定理 2 0 2 2 1 2 1 W = mv − mv 动能定理 2 0 2 2 1 2 1 W = J − J 重力势能 Ep = mgh 重力势能 Ep = mghC 机械能守恒 Ek + Ep = 恒量 只有保守力作功时 机械能守恒 Ek + Ep = 恒量 只有保守力作功时
4-4力矩作功刚体绕定轴转动的动能定 物理学教程 (第二版) 讨论 子细 圆锥摆 入 子弹击入杆 袋计 0 0 以子弹和沙袋为系统」 以子弹和杆为系统 圆锥摆系统 动量守恒; 动量不守恒; 动量不守恒; 角动量守恒; 角动量守恒; 角动量守恒; 机械能不守恒. 机械能不守恒. 机械能守恒 第四章刚体转动
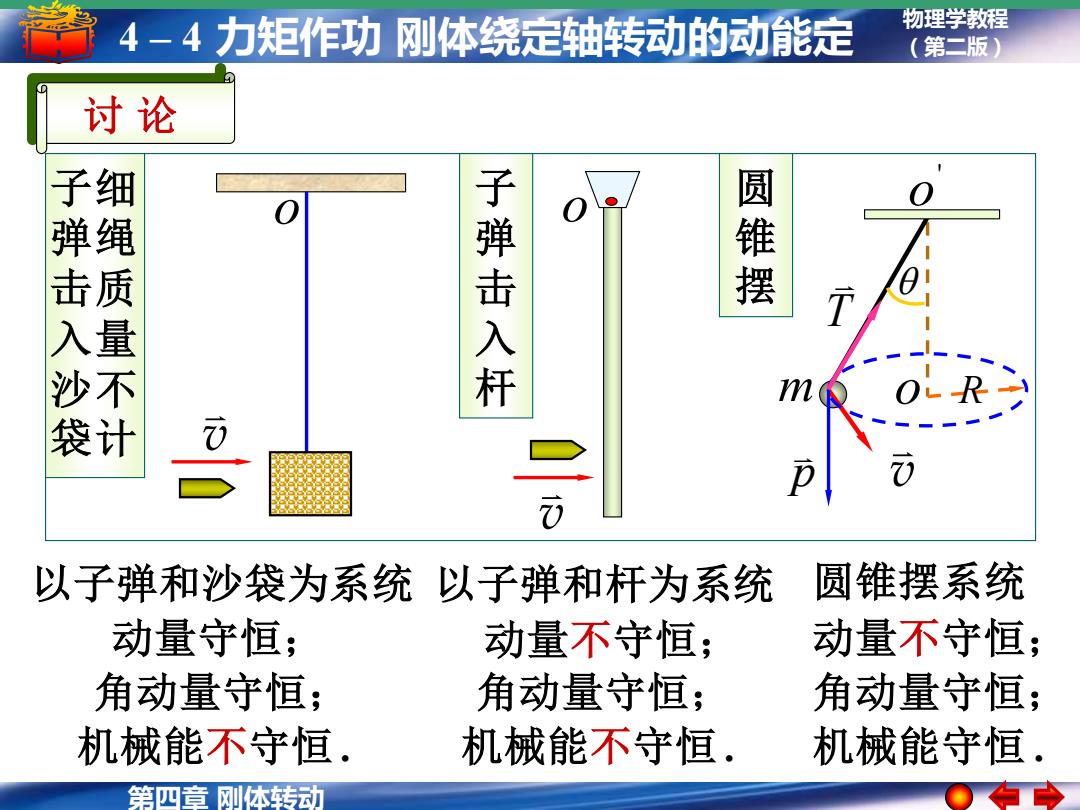
第四章 刚体转动 物理学教程 4 – 4 力矩作功 刚体绕定轴转动的动能定 (第二版) 理 v o v o ' o m p T R 圆 锥 摆 子 弹 击 入 杆 o v 以子弹和杆为系统 机械能不守恒 . 角动量守恒; 动量不守恒; 以子弹和沙袋为系统 动量守恒; 角动量守恒; 机械能不守恒 . 圆锥摆系统 动量不守恒; 角动量守恒; 机械能守恒 . 讨 论 子 弹 击 入 沙 袋 细 绳 质 量 不 计

4-4力矩作功刚体绕定轴转动的动能定 物理学教程 (第二版) 例1有一吊扇第一档转速为n1=7rad/s,第二档转 速为n2=10rad/s.吊扇转动时要受到阻力矩M的作用, 一般来说,阻力矩与转速之间的关系要由实验测定,但 作为近似计算,我们取阻力矩与角速度之间的关系为 M=ko2,其中系数k=2.74×104 N.m'rad2s2.试求 (1)吊扇的电机在这两种转速下所消耗的功率; (2)吊扇由静止匀加速地达到第二档转速经历的时间 为5s.在此时间内阻力矩做了多少功? 解(1)P=M1@=k0=k(2n)=23.3W P=Mg202 ko=k(2nn)=68.0W 第四章刚体转动
第四章 刚体转动 物理学教程 4 – 4 力矩作功 刚体绕定轴转动的动能定 (第二版) 理例1 有一吊扇第一档转速为 n1 = 7rad/s, 第二档转 速为 n2 = 10rad/s. 吊扇转动时要受到阻力矩 Mf 的作用, 一般来说, 阻力矩与转速之间的关系要由实验测定, 但 作为近似计算, 我们取阻力矩与角速度之间的关系为 Mf = k 2 , 其中系数 k = 2.74×10-4 N·m·rad-2·s2 . 试求 (1)吊扇的电机在这两种转速下所消耗的功率; (2)吊扇由静止匀加速地达到第二档转速经历的时间 为 5s . 在此时间内阻力矩做了多少功 ? 解 (1) P M k k(2πn ) 23.3W 3 1 3 1 = f1 1 = 1 = = P M k k(2πn ) 68.0W 3 2 3 2 = f 2 2 = 2 = =

4-4力矩作功刚体绕定轴转动的动能定 物理学教程 (第二版) 已知:n1=7rad/s,n2=10rad/s;M=ko2, k=2.74×104 N.m'rad-2s2.求(2)吊扇由静止匀加 速的达到第二档转速经历的时间为5s.在此时间内阻力 矩做了多少功? 解:吊扇由静止作匀角加速度运动 2元n2 a= o=at t 5 阻力矩做功 W=∫M2d6=∫kw'd w=[kat'dt=kat 4 在t=5s时间内 W=84.8J 第四章刚体转动
第四章 刚体转动 物理学教程 4 – 4 力矩作功 刚体绕定轴转动的动能定 (第二版) 理 解: 吊扇由静止作匀角加速度运动 5 2πn2 t = = W = M d = k dt 3 阻力矩做功 f 2 3 4 0 3 3 4 1 W k t dt k t t = = 在 t = 5s 时间内 W = 84.8 J 已知: n1 = 7rad/s, n2 = 10rad/s; Mf = k 2 , k = 2.74×10-4 N·m·rad-2·s2 . 求(2)吊扇由静止匀加 速的达到第二档转速经历的时间为 5s . 在此时间内阻力 矩做了多少功 ? =t
4-4力矩作功刚体绕定轴转动的动能定 物理学教程 (第二版) 例2一长为1,质量为m的竿可绕支点O自由转 动.一质量为、速率为)的子弹射入竿内距支点为 处,使竿的偏转角为30°.问子弹的初速率为多少? 解:把子弹和竿看作一个系 统·子弹射入竿的过程系统角动 量守恒 30° mva-(m'P+md)o a 3mva m'12+3ma2 第四章刚体转动
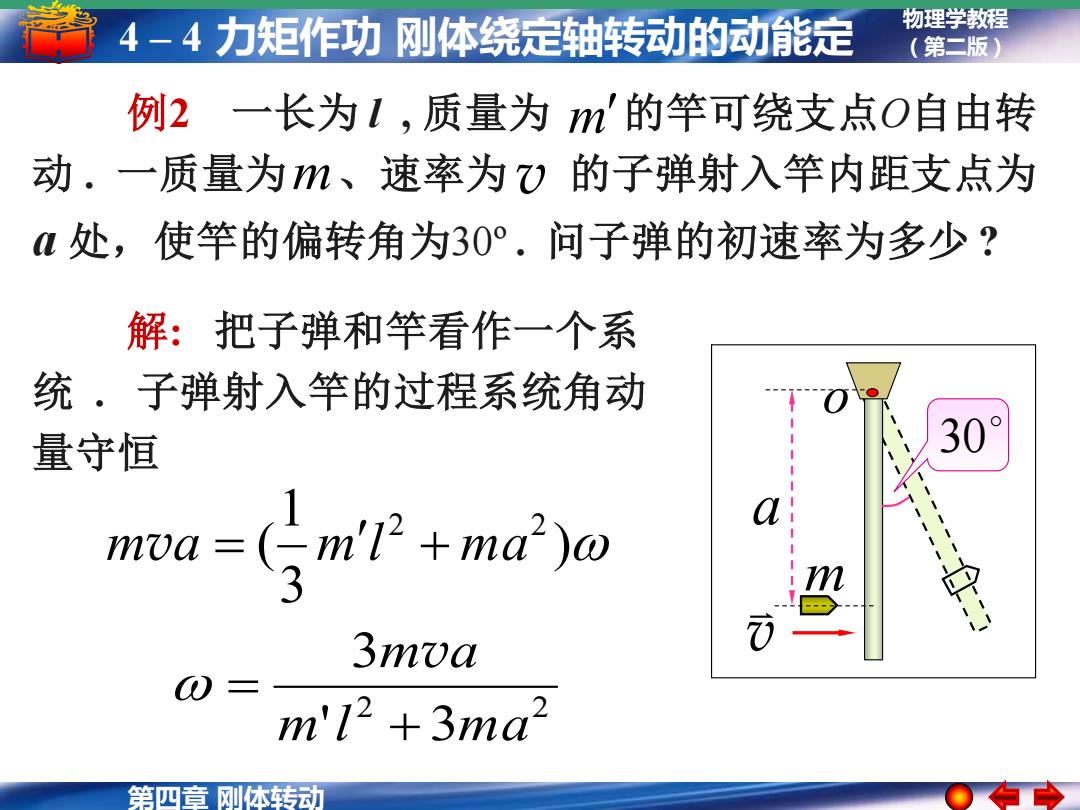
第四章 刚体转动 物理学教程 4 – 4 力矩作功 刚体绕定轴转动的动能定 (第二版) 理例2 一长为 l , 质量为 的竿可绕支点O自由转 动 . 一质量为 、速率为 的子弹射入竿内距支点为 a 处,使竿的偏转角为30º . 问子弹的初速率为多少 ? v m m 解: 把子弹和竿看作一个系 统 . 子弹射入竿的过程系统角动 量守恒 ) 3 1 ( 2 2 mva = m l + m a o a m v 30 2 2 ' 3 3 m l ma m a + = v

4-4力矩作功刚体绕定轴转动的动能定 物理学教程 (第二版) 3mva m'12+3ma2 射入竿后,以子弹、细杆和 地球为系统,机械能守恒. m 25m2+ma2a2 mga(-cs0)-c30) =g(2-13)(m'1+2ma)(m'P +3ma)/6/ma 第四章刚体转动
第四章 刚体转动 物理学教程 4 – 4 力矩作功 刚体绕定轴转动的动能定 (第二版) 理 o a m v 30 g(2 3)(m l 2ma)(m l 3ma ) 6 ma 2 2 v = − + + + = 2 2 2 ) 3 1 ( 2 1 m l ma (1 cos30 ) 2 + − l mga(1− cos30) m g 射入竿后,以子弹、细杆和 地球为系统 ,机械能守恒 . 2 2 ' 3 3 m l ma m a + = v