3-5保守力与非保守力势能 物理学教程 (第二版) 万有引力、重力、弹性力作功的特点 1)万有引力作功 以m为参考系,m的位置矢量为r. m对m的万有引力为 m r(t F=-G m'm r方向单 e. r2 位矢量 F(t+dt) m移动d时,作元功为 m'm Le.dF B dW=F.d时=-G 第三章动量守恒定律和能量守恒定律
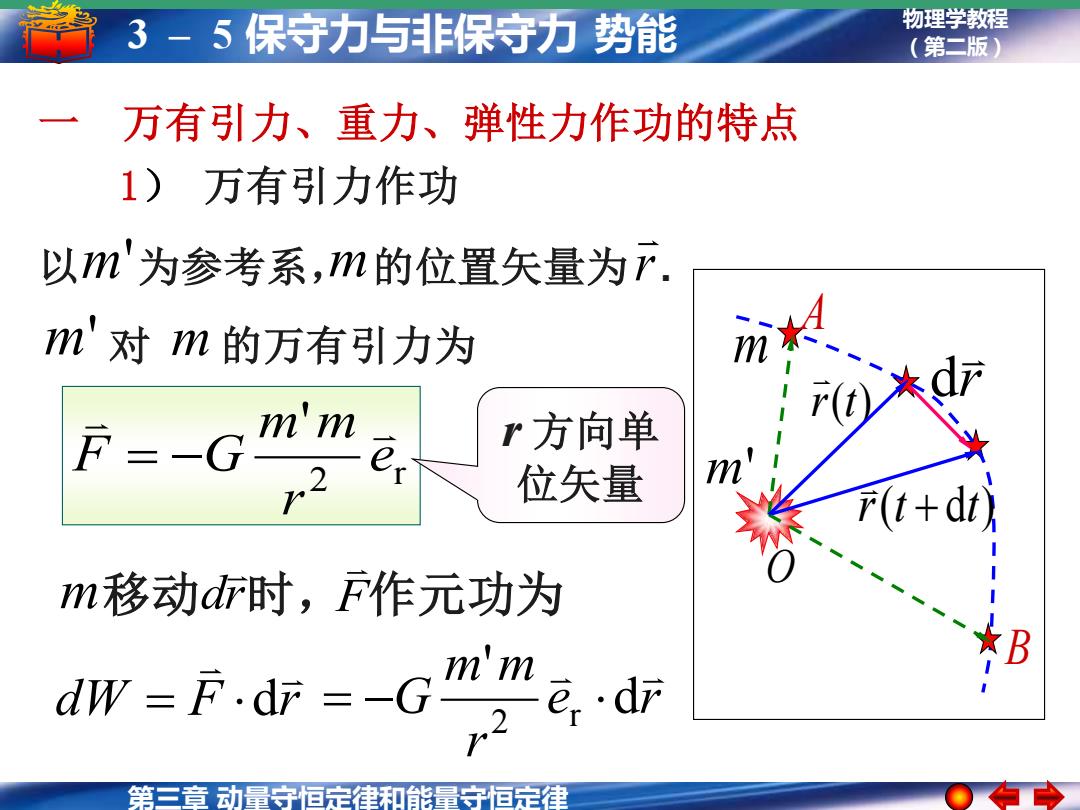
第三章 动量守恒定律和能量守恒定律 物理学教程 3 – 5 保守力与非保守力 势能 (第二版) 1) 万有引力作功 以 为参考系, 的位置矢量为 r. m' m 一 万有引力、重力、弹性力作功的特点 m' 对 m 的万有引力为 2 r ' e r m m F G = − dW F r = d e r r m m G d ' 2 r = − m 移动 时, F 作元功为 dr r(t) r(t + dt) r d m O m' A B r 方向单 位矢量
3-5保守力与非保守力势能 物理学教程 (第二版) -fF.dF--Ge.dF r(i e·d=e:d cosp=dr r(t+dt) -6 *B 0-0] r(t+dt) 第三章动量守恒定律和能量守恒定律
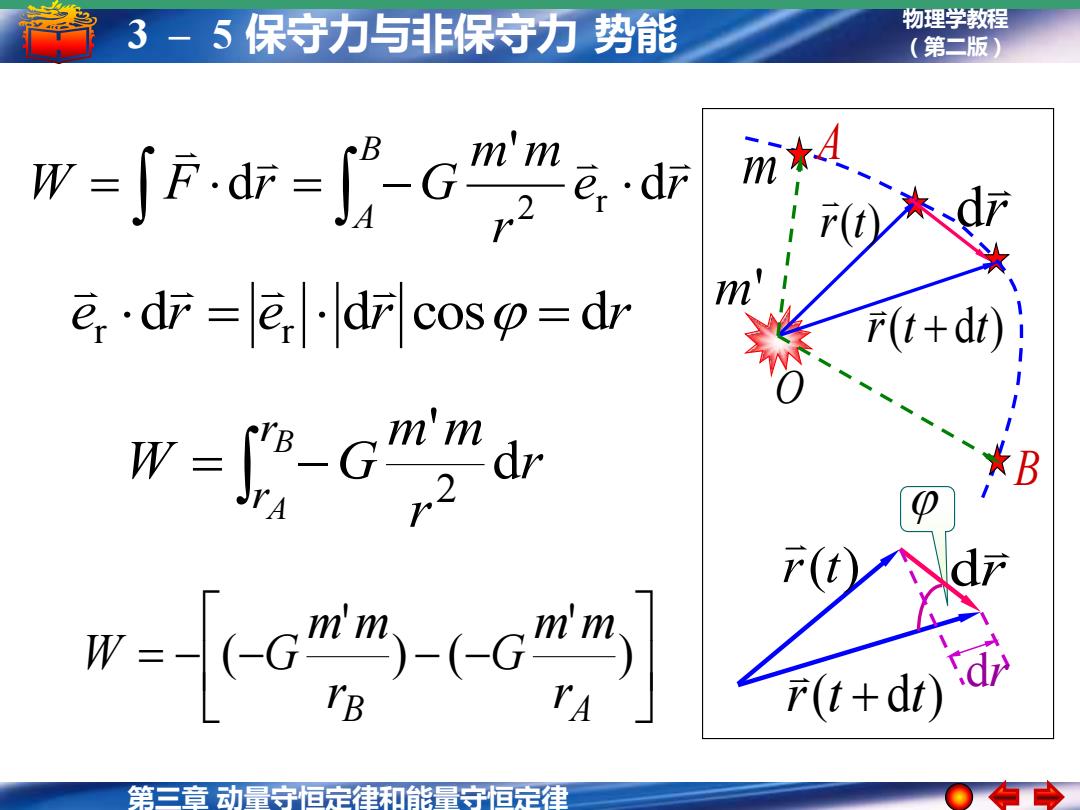
第三章 动量守恒定律和能量守恒定律 物理学教程 3 – 5 保守力与非保守力 势能 (第二版) = − − − − ) ' ) ( ' ( B A r m m G r m m W G = − B A r r r r m m W G d ' 2 e dr e dr cos dr r = r = = = − B A e r r m m W F r G d ' d 2 r r(t) r(t + dt) r d m O m' A B r(t) r(t + dt) r d dr
3-5保守力与非保守力势能 物理学教程 (第二版) 2) 重力作功 19 P=-mgj dr dxi +dyj w=n.d正=-mgd =-(mgyg-mgy) W=∮-mgdy=0 第三章动量守恒定律和能量守恒定建
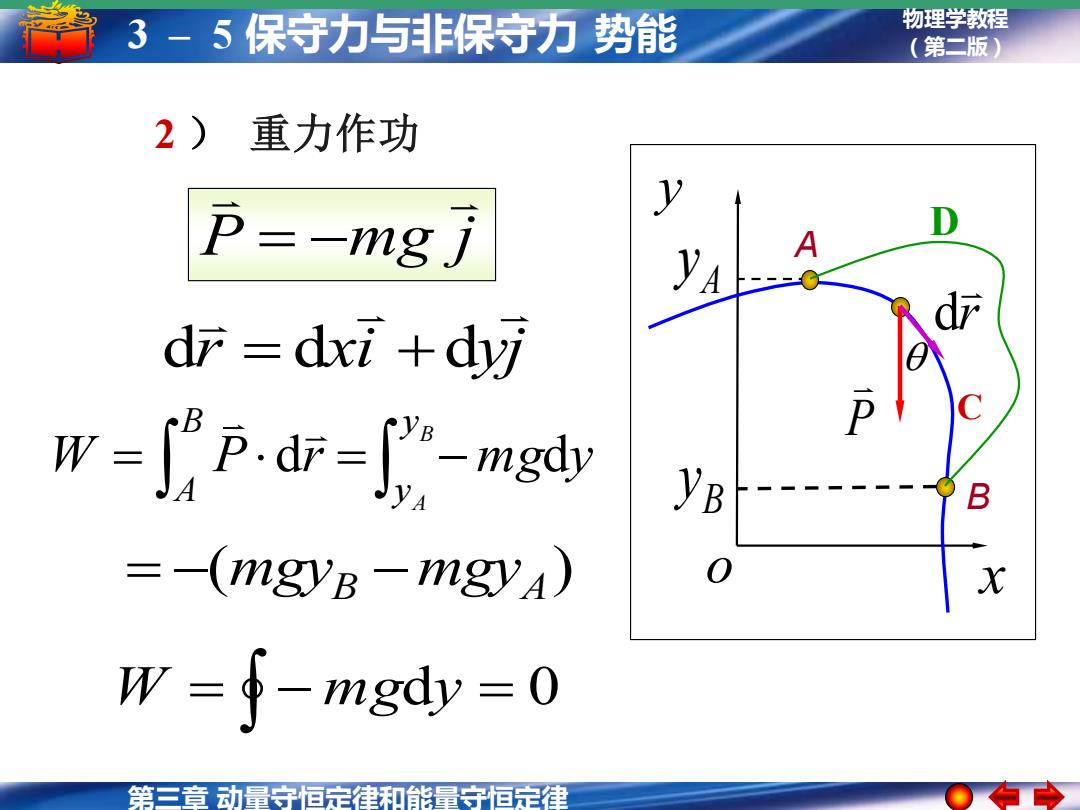
第三章 动量守恒定律和能量守恒定律 物理学教程 3 – 5 保守力与非保守力 势能 (第二版) = − d = 0 W m g y r xi yj d = d +d ( ) = − mgyB −mgyA P mg j = − W P r m g y B A y y B A d d = = − 2 ) 重力作功 A B A y B y P o x y r d D C
3-5保守力与非保守力势能 物理学教程 (第二版) 3)弹性力作功 dw形 A具FF O XA XB X dx xB 疗=-kxi w rid=-oxcds w=-5-a)月 =g-kxdx=0 第三章动量守恒定律和能量守恒定律
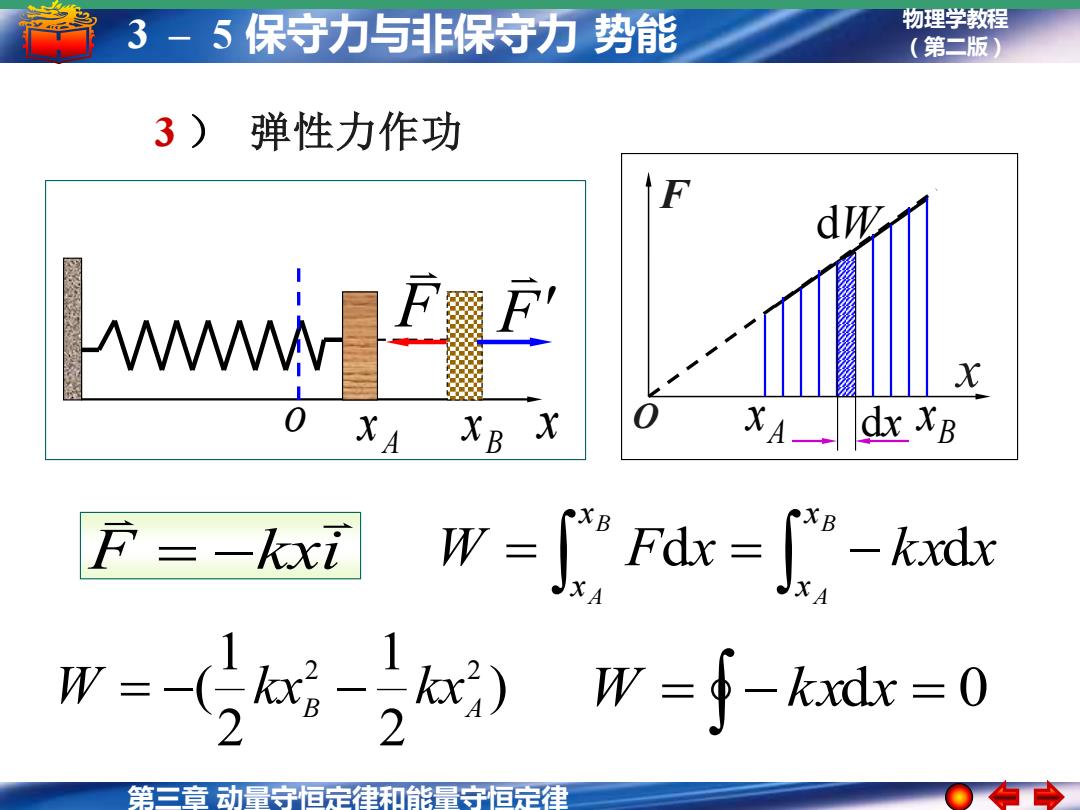
第三章 动量守恒定律和能量守恒定律 物理学教程 3 – 5 保守力与非保守力 势能 (第二版) = − d = 0 W k x x F kxi = − = = − B A B A x x x x W Fdx k xdx ) 2 1 2 1 ( 2 2 B A W = − kx − kx 3 ) 弹性力作功 A x B x F o x F x dx dW O A x B x F
3-5保守力与非保守力势能 物理学教程 (第二版) 二 保守力和非保守力 > 保守力:力所作的功与路径无关,仅决定于相 互作用质点的始末相对位置. =-6-620 重力功W=-(mgyB-mgyA) 力功=(x-c) FFFd 第三章动量守恒定律和能量守恒定律
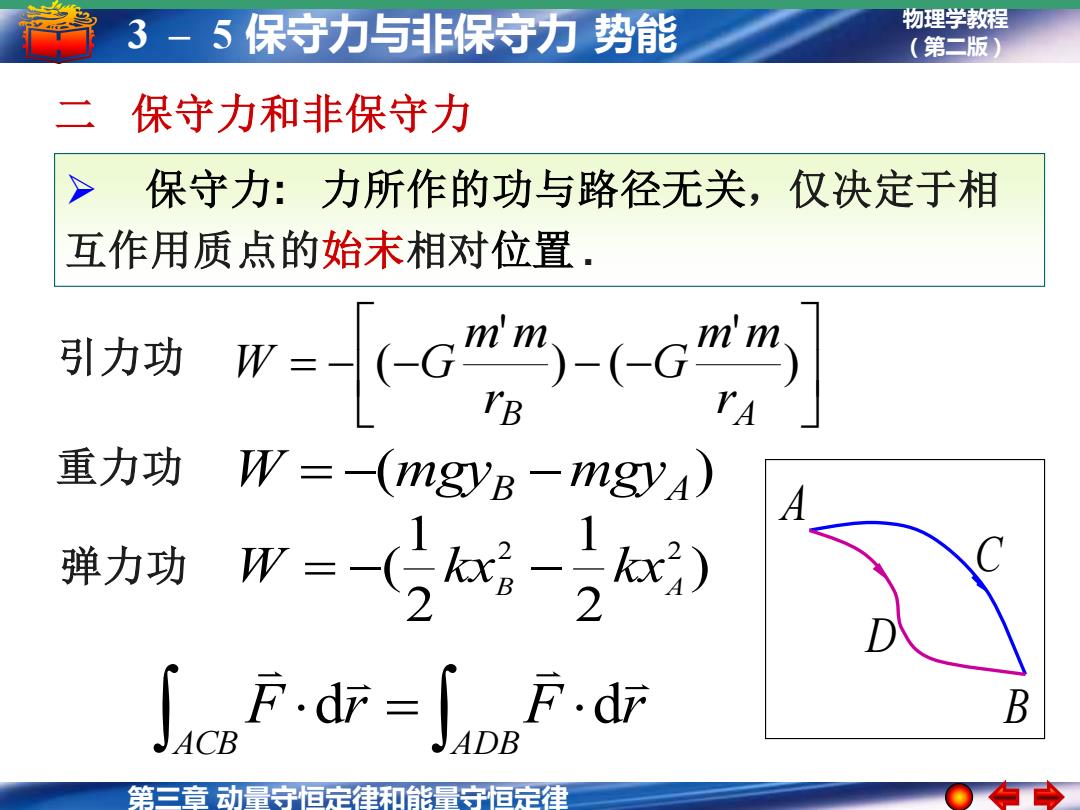
第三章 动量守恒定律和能量守恒定律 物理学教程 3 – 5 保守力与非保守力 势能 (第二版) ➢ 保守力: 力所作的功与路径无关,仅决定于相 互作用质点的始末相对位置 . 二 保守力和非保守力 ) 2 1 2 1 ( 2 2 B A W = − kx − kx = − − − − ) ' ) ( ' ( B A r m m G r m m W G ( ) 重力功 W = − mgyB −mgyA 弹力功 引力功 = ACB ADB F r F r d d A B C D
3-5保守力与非保守力势能 物理学教程 (第二版) ∫c京dr=jnF-d fF.d=天dr+天d fF.dF-0 物体沿闭合路径运动一周时, 保守力对它所作的功等于零 >非保守力:力所作的功与路径有关.(例如摩擦力) 第三章动量守恒定律和能量守恒定律
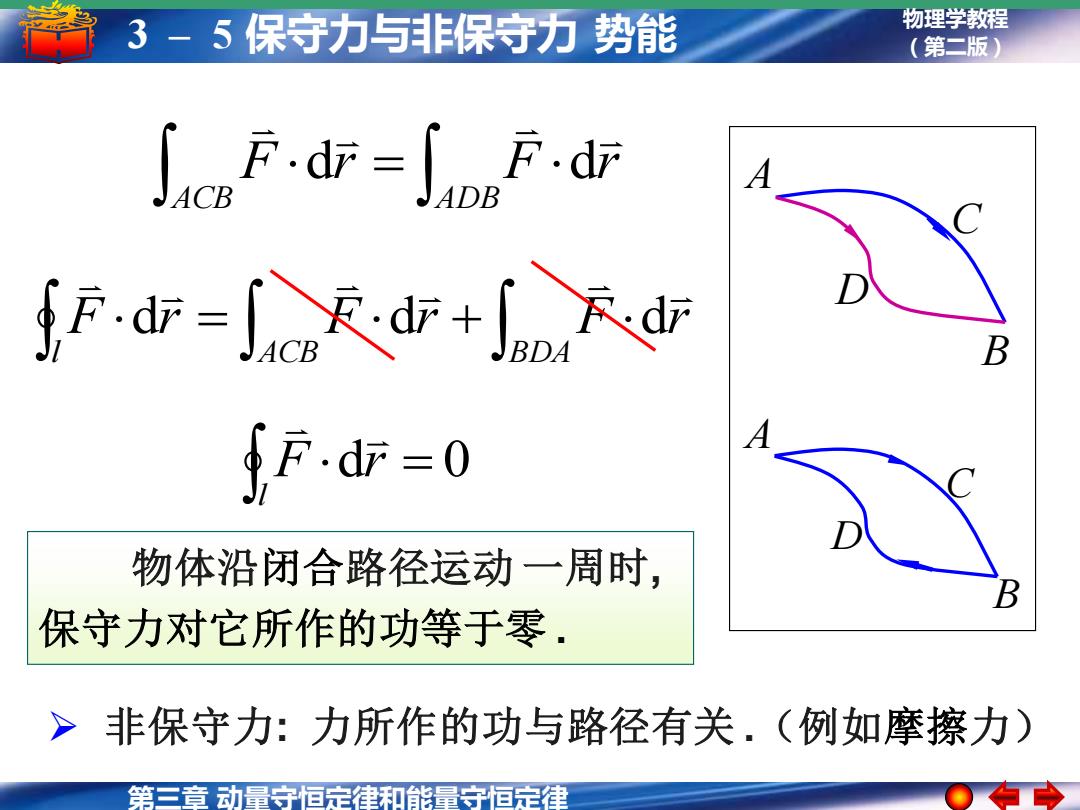
第三章 动量守恒定律和能量守恒定律 物理学教程 3 – 5 保守力与非保守力 势能 (第二版) A B C D ➢ 非保守力: 力所作的功与路径有关 .(例如摩擦力) 物体沿闭合路径运动 一周时, 保守力对它所作的功等于零 . d = 0 l F r = + l ACB BDA F r F r F r d d d A B C D = ACB ADB F r F r d d

3-5保守力与非保守力势能 物理学教程 (第二版) 势能 三 势能曲线 ◆势能 与物体间相互作用及相对位置有关的能量. 重力功 重力势能 W=-(1mgyB-ngyA) Ep mgz 引力功 引力势能 w=-i69(c Ep=-G m'm 弹力功 弹性势能 W kx? 保守力的功 W=-(Ep2-Ep)=-AEp 第三章动量守恒定律和能量守恒定律
第三章 动量守恒定律和能量守恒定律 物理学教程 3 – 5 保守力与非保守力 势能 (第二版) 三 势能 势能曲线 势能 与物体间相互作用及相对位置有关的能量 . p2 p1 P 保守力的功 W = −(E − E ) = −E 弹性势能 2 p 2 1 E = k x 引力势能 r m m E G ' p = − 重力势能 E = mgz p ) 2 1 2 1 ( 2 2 B A W = − k x − k x 弹力功 = − − − − ) ' ) ( ' ( B A r m m G r m m W G 引力功 ( ) W = − mgyB −mgyA 重力功

-5保守力与非保守力势能 3 物理学教程 (第二版) 讨论 势能是状态函数 Ep =Ep(x,y,2) ◆势能具有相对性,势能大小与势能零点的选取有关. ◆势能是属于系统的. ◆势能计算 W=-(Ep-E0)=-△Ep 若令Ep0(xo,y0,z0)=0 Ep(x,y,2)= %o。d J(x,y.z) 第三章动量守恒定律和能量守恒定律
第三章 动量守恒定律和能量守恒定律 物理学教程 3 – 5 保守力与非保守力 势能 (第二版) 势能具有相对性,势能大小与势能零点的选取有关 . ( , , ) p p 势能是状态函数 E = E x y z 势能是属于系统的 . 讨论 势能计算 p p0 p W = −(E − E ) = −E = ( , , ) ( , , ) p c 0 0 0 ( , , ) d x y z x y z E x y z F r 若令 Ep0 (x0 , y0 ,z0 ) = 0

3-5保守力与非保守力势能 物理学教程 (第二版) > 势能曲线:由势能函数确定的势能随坐标变化的曲线 Ep =mgy E。 E。=-G 'm E X 重力势能曲线 弹性势能曲线 引力势能曲线 y=0,E。=0 x=0,E。=0 r→0,E,=0 第三章动量守恒定律和能量守恒定律
第三章 动量守恒定律和能量守恒定律 物理学教程 3 – 5 保守力与非保守力 势能 (第二版) Ep y O E = mgy p 弹性势能曲线 x = 0, Ep = 0 重力势能曲线 0, 0 y = Ep = 引力势能曲线 , 0 r → Ep = x O Ep 2 p 2 1 E = k x x O Ep r m m E G ' p = − ➢ 势能曲线:由势能函数确定的势能随坐标变化的曲线