
3-4动能定理 物理学教程 (第二版) 力的空间累积效应 W,E,动能定理等 功 力对质点所作的功为力在质点位移方向的分量与 位移大小的乘积.(功是标量,过程量) dw Fcosdr=Fcos ds d B dw=F.dr 0°0 90°<0<180°,dW<0 dr 、0=90°F⊥dFdW=0 第三章动量守恒定律和能量守恒定律
第三章 动量守恒定律和能量守恒定律 物理学教程 3 – 4 动能定理 (第二版) 力对质点所作的功为力在质点位移方向的分量与 位移大小的乘积 . (功是标量,过程量) dW = F cos dr = F cos ds W F r d = d 一 功 力的空间累积效应 W , E ,动能定理等. F r d Fi 1 dr i r d B * * i 1 A F1 0 90 , dW 0 90 180 , dW 0 = 90 F ⊥ dr dW = 0

物理学教程 3-4动能定理 (第二版) 。 变力的功 dw=F.dr Fcos0 W=∫F.d=∫Fcos0ds ·合力的功=分力的功的代数和 ds SB W=∫∑F·dF=∑∫Fd产=∑W F=+E7+:K Ldr dxi dyj +dzk W=∫Fdx+∫F,dy+JFdz W-W.+W.+W. 第三章动量守恒定律和能量守恒定律
第三章 动量守恒定律和能量守恒定律 物理学教程 3 – 4 动能定理 (第二版) = = = i i i Wi W F r F r d d W = F x + F y + F z x d y d z d W =W x +W y +W z r xi yj zk d = d + d + d F F i F j F k x y z = + + = = B A B A W F dr F cos ds • 合力的功 = 分力的功的代数和 Fcos A s B s ds s o • 变力的功 W F r d = d

物理学教程 3-4动能定理 (第二版) ◆功的大小与参照系有关 ◆功的量纲和单位dimW=ML2T-2lJ=1N·m ◆平均功率 P= △W △t △W dw ◆瞬时功率 P=lim △t→0 △t dt P-FucosO ◆功率的单位(瓦特)1W=1J.s1 1kW=103W 第三章动量守恒定律和能量守恒定律
第三章 动量守恒定律和能量守恒定律 物理学教程 3 – 4 动能定理 (第二版) 功的大小与参照系有关 dim ML T 1J 1N m 2 2 = = − 功的量纲和单位 W t W P 平均功率 = 瞬时功率 v = = = → F t W t W P t d d lim 0 P = Fvcos 功率的单位 (瓦特) 1W =1Js −1 1kW =103W

物理学教程 3-4动能定理 (第二版) 例1质量为2kg的物体由静止出发沿直线运动,作 用在物体上的力为F=6tN).试求在头2秒内,此力 对物体做的功: 解: a,=F,/m=3t dv a= dt do=3idt v=1.5t2 dx =v.dt =1.5t2dt W=∫Fdx=9rf=36.0J 第三章动量守恒定律和能量守恒定律
第三章 动量守恒定律和能量守恒定律 物理学教程 3 – 4 动能定理 (第二版) 例1 质量为 2kg 的物体由静止出发沿直线运动, 作 用在物体上的力为 F = 6 t (N) . 试求在头 2 秒内, 此力 对物体做的功. a F m t x x = = 3 t a d dv = = t t 0 dv 3 dt vx 0 2 =1.5t vx d d 1.5t dt 2 x = vx t = d 9 d 36.0 J 2 0 3 = = = W F x t t 解:

3-4动能定理 物理学教程 (第二版) 二质点的动能定理 dv m=∫F.d=∫Fld时=∫Fds F=m dt R-mgds-=八mwt= 2 2 动能(状态函数) Ek= 1 2 2m 动能定理 合外力对质点所作的功, 等于质点动能的增量. W=Ek2-Ek 功和动能都与参考系有关;动能定理 仅适用于惯性系 动量守恒定律和能量守恒定律
第三章 动量守恒定律和能量守恒定律 物理学教程 3 – 4 动能定理 (第二版) 二 质点的动能定理 2 1 2 2 2 1 2 1 d d d d 2 1 2 1 v v v v v v v v v s m m m t W = m = = − 动能(状态函数) m p E m 2 2 1 2 2 k = v = t F m d d t v W F dr F dr F ds = = t = t = 动能定理 W = Ek2 −Ek1 合外力对质点所作的功, 等于质点动能的增量 . 功和动能都与 参考系有关;动能定理 仅适用于惯性系 . 注意

物理学教程 3-4动能定理 (第二版) 例2一质量为1.0kg的小球系在长为1.0m细绳下 端,绳的上端固定在天花板上.起初把绳子放在与竖直 线成30°角处,然后放手使小球沿圆弧下落.试求绳与 竖直线成10°角时小球的速率. 解:dW=Fd=Fd+Pd5 =P.ds=-mgldecoso =-mglsinθd0 w =-mgl["sin 0d0 -mgl(cos 0-cos) 第三章动量守恒定律和能量守恒定律
第三章 动量守恒定律和能量守恒定律 物理学教程 3 – 4 动能定理 (第二版) P 例 2 一质量为1.0kg 的小球系在长为1.0m 细绳下 端 , 绳的上端固定在天花板上 . 起初把绳子放在与竖直 线成 角处, 然后放手使小球沿圆弧下落 . 试求绳与 竖直线成 角时小球的速率 . 30 10 W F s F s P s d d d d T 解: = = + (cos cos ) = mgl − 0 = Pd s = −mgl d cos = −mglsin d = − 0 W mgl sin d d l 0 v FT s d
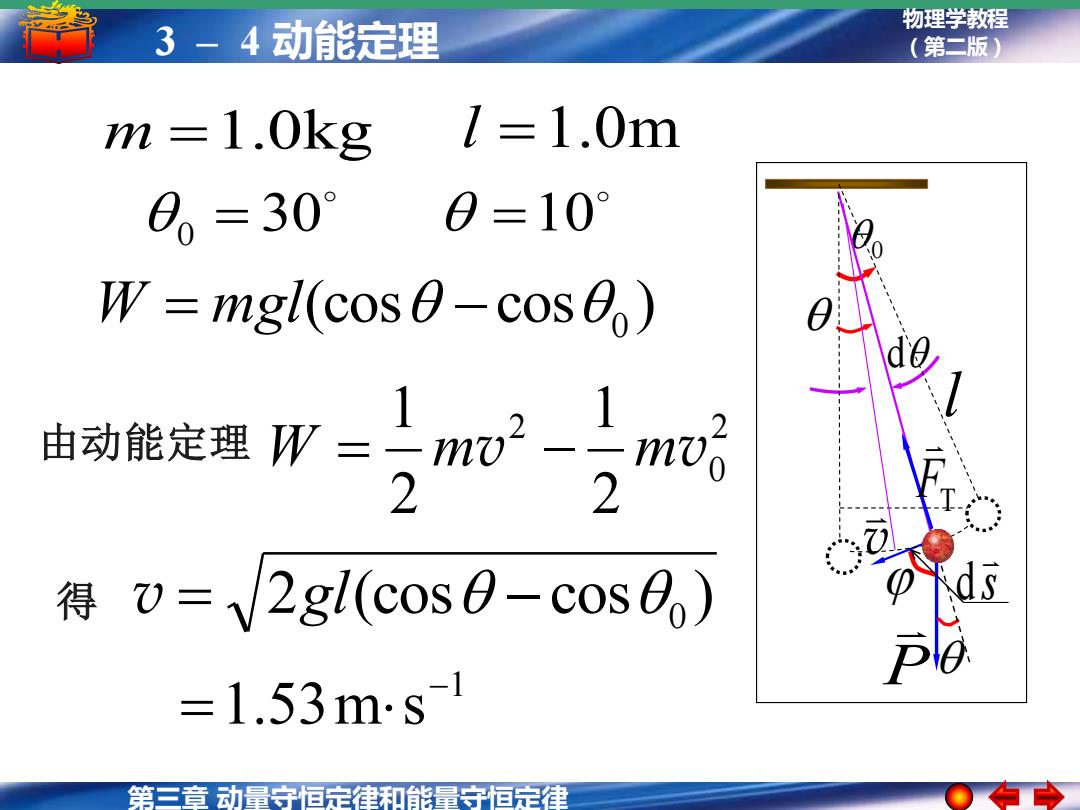
-4动能定理 物理学教程 3 (第二版) m =1.0kg l=1.0m 0。=30° 0=10° W mgl(cos0-cos) 由动能定理W= mo-m 2 得0=V2gl(cos0-cos0) =1.53ms1 第三章动量守恒定律和能量守恒定律
第三章 动量守恒定律和能量守恒定律 物理学教程 3 – 4 动能定理 (第二版) (cos cos ) W = mgl − 0 由动能定理 2 0 2 2 1 2 1 W = mv − mv 得 2 (cos cos ) v = gl − 0 1 1.53m s − = P d l 0 v FT s d m =1.0kg l =1.0m 0 = 30 =10