
5-1简谐运动简谐运动的振幅周期频率和相位 物理学教程 (第二版) 任一物理量在某一定值附近往复变化均称为振动, 机械振动 物体围绕一固定位置往复运动. 运动形式:直线、平面和空间振动, 例如一切发声体、心脏、海浪起伏、地震以及晶体 中原子的振动等 周期和非周期振动 简谐运动 最简单、最基本的振动、 合成 简谐运动 复杂振动 分解 谐振子:作简谐运动的物体 第五章机械振动
物理学教程 (第二版) 第五章 机械振动 5 – 1 简谐运动 简谐运动的振幅 周期 频率和相位 任一物理量在某一定值附近往复变化均称为振动. 机械振动 物体围绕一固定位置往复运动. 运动形式: 直线、平面和空间振动. 周期和非周期振动 简谐运动 最简单、最基本的振动. 谐振子: 作简谐运动的物体. 例如一切发声体、心脏、海浪起伏、地震以及晶体 中原子的振动等. 简谐运动 复杂振动 合成 分解
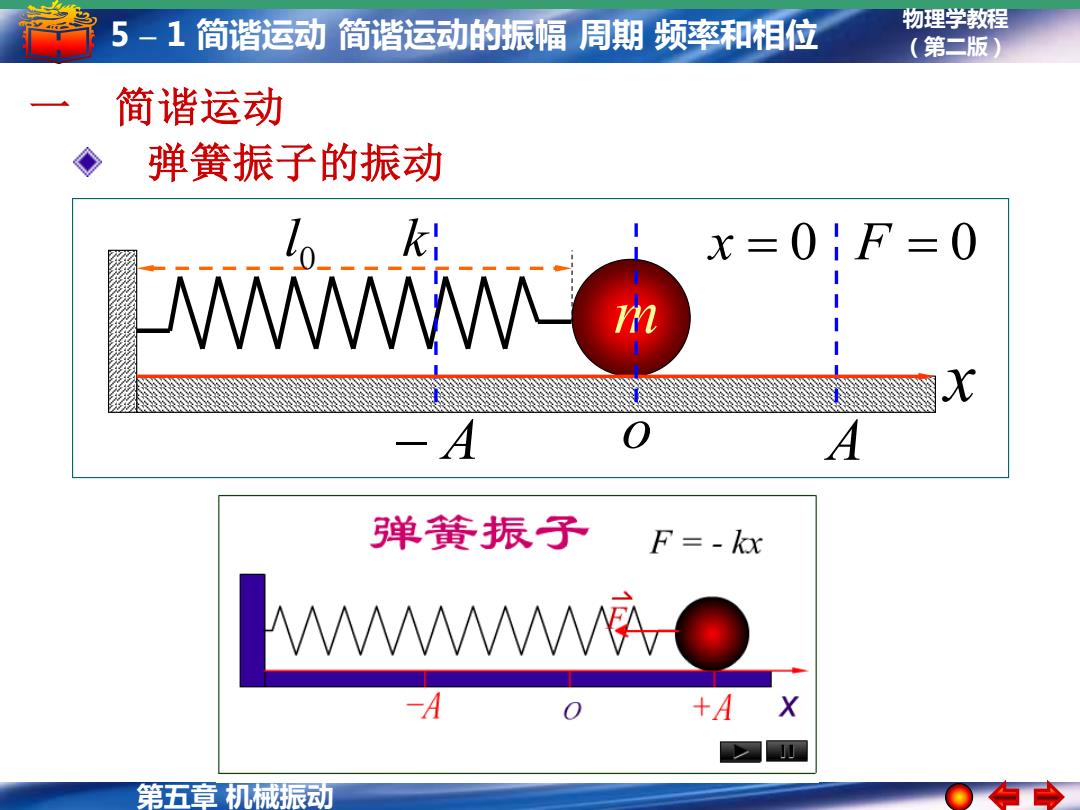
5-1简谐运动简谐运动的振幅周期频率和相位 物理学教程 (第二版) 简谐运动 弹簧振子的振动 lo ki x=01F=0 M -A A 弹簧振子 F=-kx M -A +A 第五章机械振动
物理学教程 (第二版) 第五章 机械振动 5 – 1 简谐运动 简谐运动的振幅 周期 频率和相位 l k 0 x m − A o A 弹簧振子的振动 x = 0 F = 0 一 简谐运动
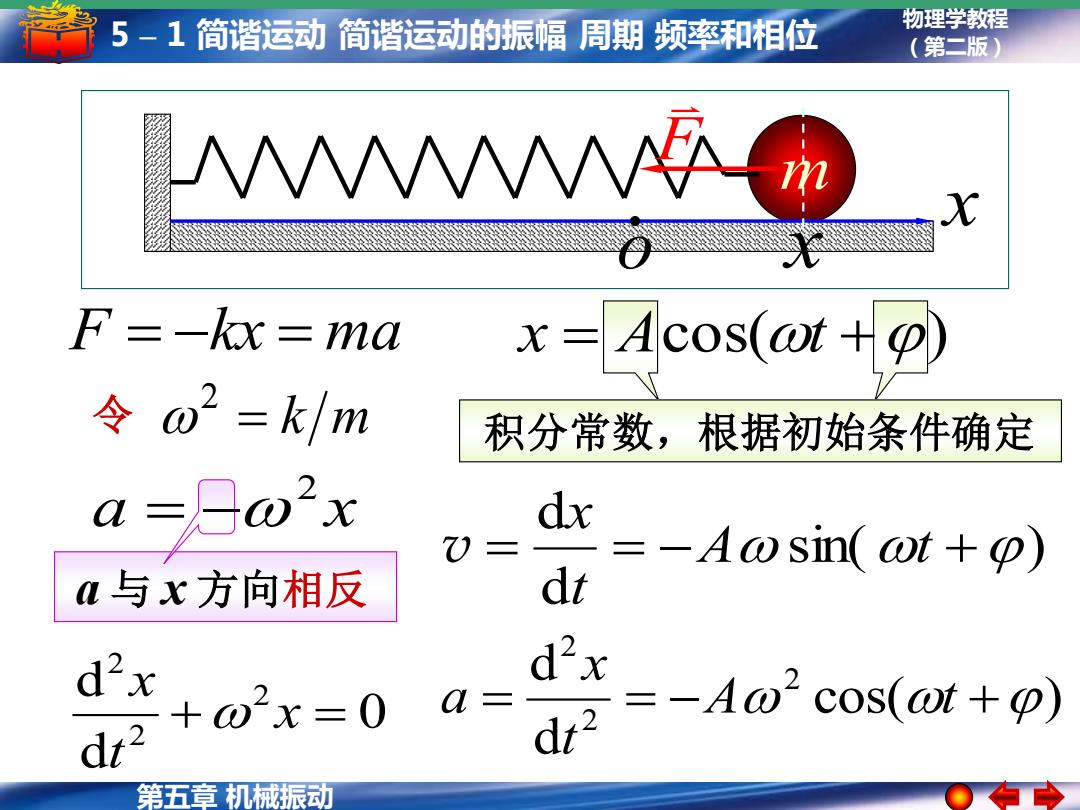
5-1简谐运动简谐运动的振幅周期频率和相位 物理学教程 (第二版) V F=-kx =ma x=Acos(or Ho) 令o2=k/m 积分常数,根据初始条件确定 a=3ω2x dx M与x方向相反 dt =-Aosin(at+) d2x d2x +0x=0 a dt2 dt2 =-Ao2cos(@t+p) 第五章机械振动
物理学教程 (第二版) 第五章 机械振动 5 – 1 简谐运动 简谐运动的振幅 周期 频率和相位 F = −kx = ma0 d d 2 2 2 + x = t x = k m 2 令 sin( ) d d = = −A t + t x v cos( ) d d 2 2 2 = = −A t + t x a 积分常数,根据初始条件确定 x = Acos(t +) x x F m o a 与 x 方向相反 a x 2 = −
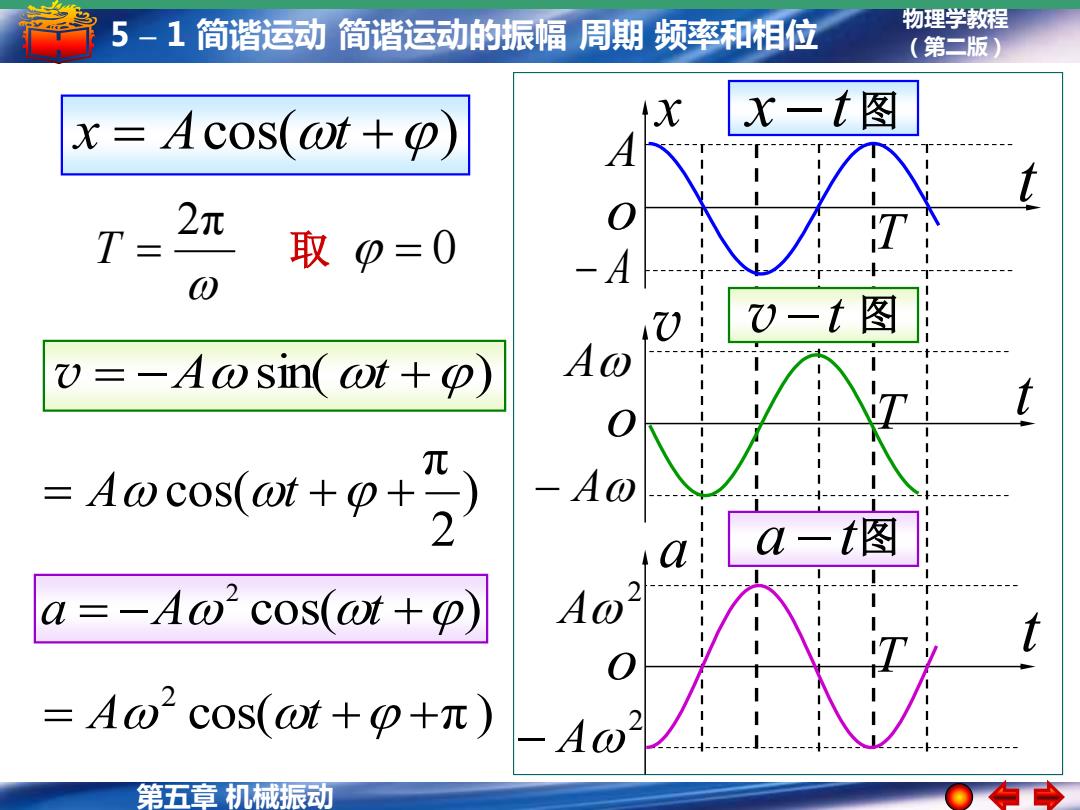
5-1简谐运动简谐运动的振幅周期频率和相位 物理学教程 (第二版) x=Acos(@t+p) x一t图 T= 2元 取0=0 -A )-t图 =-A0sin(at+o) Aocos(wt+ -A0 aLa-t图 a=-A0 cos(at+o) A1 =Ao2cos(ot+p+元) -A0 第五章机械振动
物理学教程 (第二版) 第五章 机械振动 5 – 1 简谐运动 简谐运动的振幅 周期 频率和相位 x −t 图 v −t 图 a −t 图 T A − A 2 A 2 − A x v a t t t A − A o o o T T x = Acos(t +) 取 = 0 2π T = ) 2 π = A cos(t + + v = −A sin(t +) cos( π ) 2 = A t + + cos( ) 2 a = −A t +
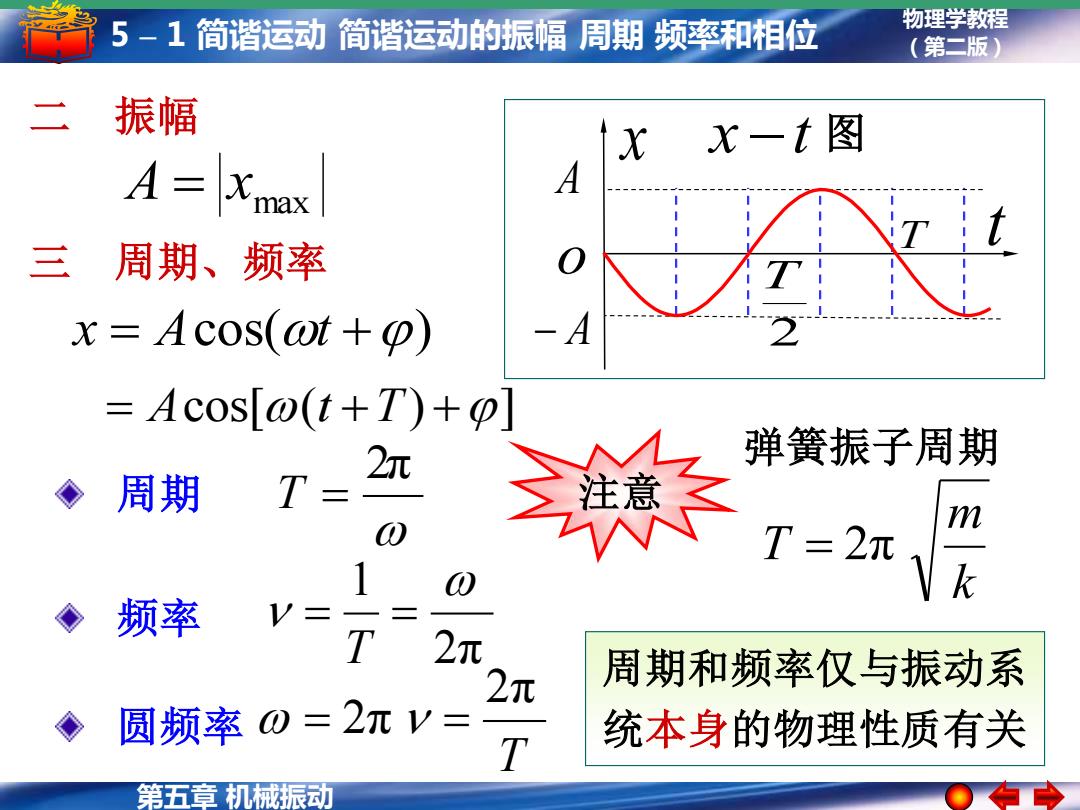
5-1简谐运动简谐运动的振幅周期频率和相位 物理学教程 (第二版) 二 振幅 X x一t图 A 三 周期、频率 x=Acos(ot+) Acos[o(t+T)+@] 弹簧振子周期 >周期 T= 2π m T=2π 1 k 频率 V= 2元 2元 周期和频率仅与振动系 圆频率0=2πV= T 统本身的物理性质有关 第五章机械振动
物理学教程 (第二版) 第五章 机械振动 5 – 1 简谐运动 简谐运动的振幅 周期 频率和相位 x = Acos(t +) 二 振幅 max A = x 三 周期、频率 k m T = 2π 弹簧振子周期 2π 周期 T = 2π 1 = = T 频率 T 2π 圆频率 = 2π = = Acos[(t +T) +] 周期和频率仅与振动系 统本身的物理性质有关 注意 x −t 图 A − A x T 2 T t o
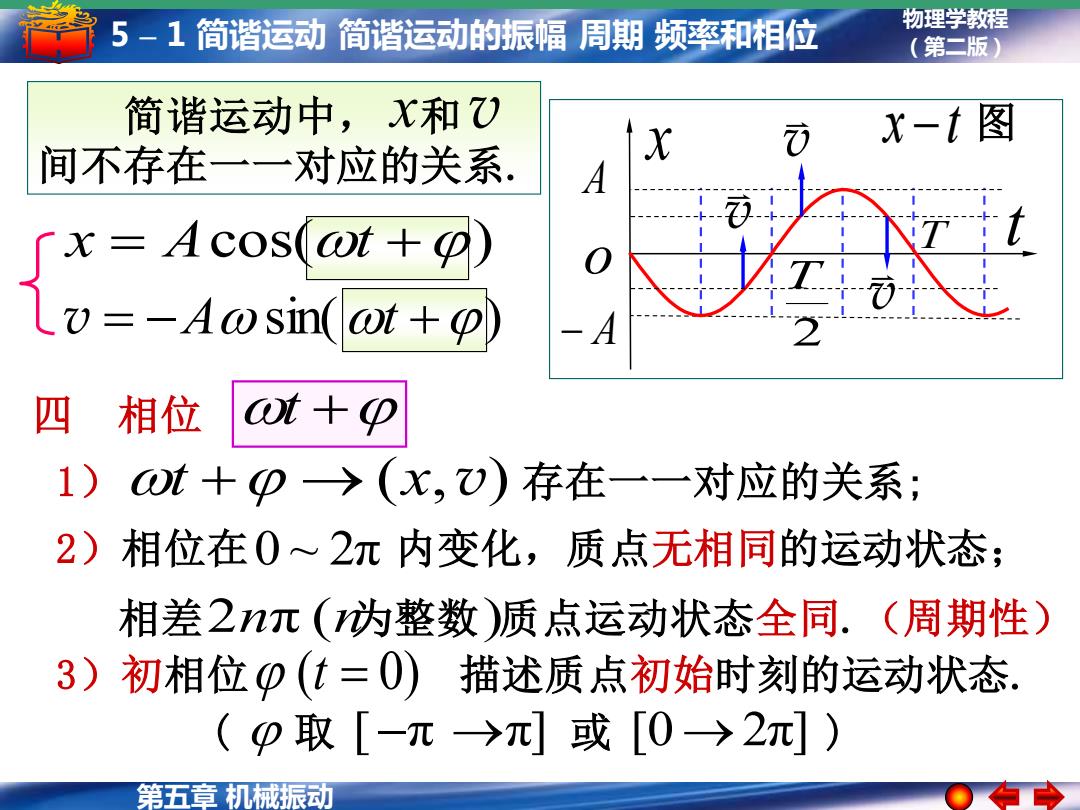
5-1简谐运动简谐运动的振幅周期频率和相位 物理学教程 (第二版) 简谐运动中,X和) 间不存在一一对应的关系. X x-t图 A x-Acos(ot+) Lv=-Awsin(at+p) 四 相位 at+o 1) ⊙t+D>(x,)存在一一对应的关系; 2)相位在0~2元内变化,质点无相同的运动状态; 相差2n元(为整数)质点运动状态全同.(周期性) 3) 初相位0(t=0)描述质点初始时刻的运动状态. (p取[-元>元]或[0→2π]) 第五章机械振动
物理学教程 (第二版) 第五章 机械振动 5 – 1 简谐运动 简谐运动的振幅 周期 频率和相位 1) t + → (x,v) 存在一一对应的关系; 2)相位在 0 ~ 2π 内变化,质点无相同的运动状态; 四 相位 t + 3)初相位 (t = 0) 描述质点初始时刻的运动状态. 相差 2nπ (n 为整数 ) 质点运动状态全同.(周期性) ( 取 [−π →π] 或 [0→2π] ) x −t 图 A − A x T 2 T t o v = −A sin(t +) x = Acos(t +) 简谐运动中, 和 间不存在一一对应的关系. x v v v v

5-1简谐运动简谐运动的振幅周期频率和相位 物理学教程 (第二版) 五常数A和①的确定 +o则 初始条件t=0x=x,)=Vo 0 6=1cS0 vo =-@Asin p tan⑩ 00 WXo 对给定振动系统,周期由系统本身性质决定, 振幅和初相由初始条件决定. 第五章机械振动
物理学教程 (第二版) 第五章 机械振动 5 – 1 简谐运动 简谐运动的振幅 周期 频率和相位 2 2 2 0 0 v A = x + 0 0 tan x − v = 五 常数 A 和 的确定 = 0 = 0 v = v0 初始条件 t x x x0 = Acos v0 = −Asin 对给定振动系统,周期由系统本身性质决定, 振幅和初相由初始条件决定. v = −A sin(t +) x = Acos(t +)

5-1简谐运动简谐运动的振幅周期频率和相位 物理学教程 (第二版) 讨论 已知t=0,x=0,)0取p= A 2 x=Acos() 第五章机械振动
物理学教程 (第二版) 第五章 机械振动 5 – 1 简谐运动 简谐运动的振幅 周期 频率和相位 0 = Acos 2 π = v0 = −Asin 0 2 π sin 0 取 = 讨论 已知 t = 0, x = 0, v 0 求 x v o ) 2 π x = Acos(t + A − A x T 2 T t o
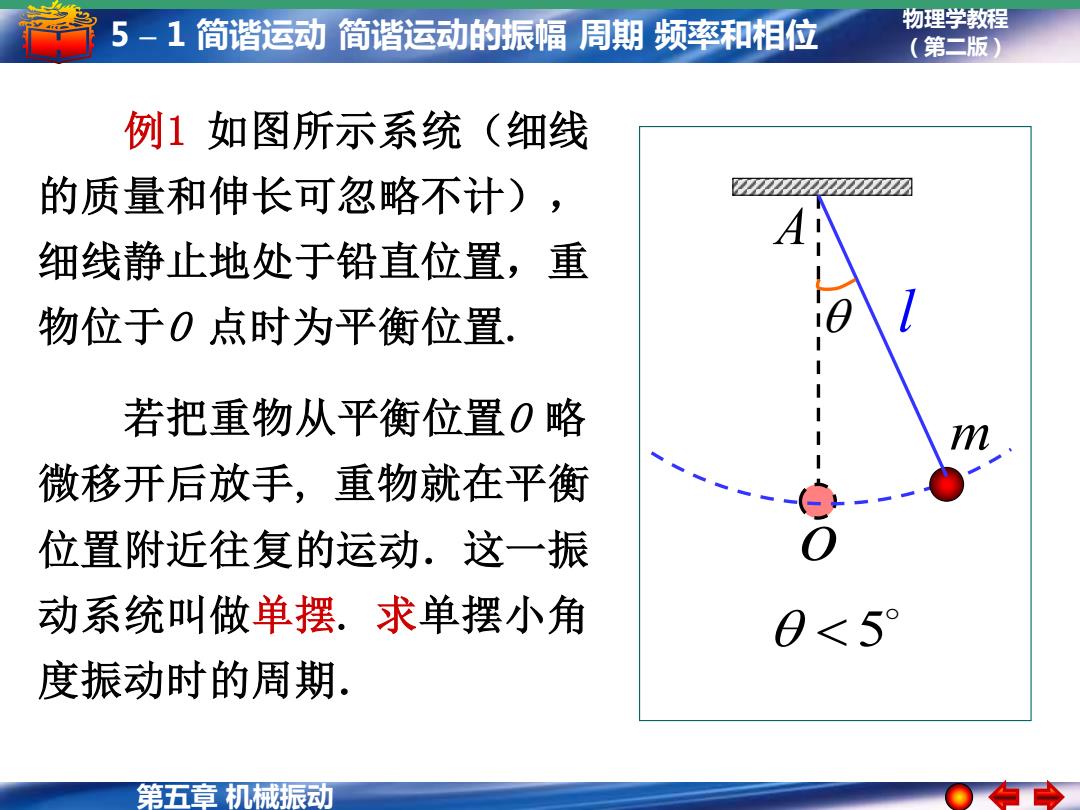
5-1简谐运动简谐运动的振幅周期频率和相位 物理学教程 (第二版) 例1如图所示系统(细线 的质量和伸长可忽略不计), ☑ 细线静止地处于铅直位置,重 物位于O点时为平衡位置. 若把重物从平衡位置O略 微移开后放手,重物就在平衡 位置附近往复的运动.这一振 动系统叫做单摆.求单摆小角 0≤5° 度振动时的周期. 第五章机械振动
物理学教程 (第二版) 第五章 机械振动 5 – 1 简谐运动 简谐运动的振幅 周期 频率和相位 例1 如图所示系统(细线 的质量和伸长可忽略不计), 细线静止地处于铅直位置,重 物位于O 点时为平衡位置. 若把重物从平衡位置O 略 微移开后放手, 重物就在平衡 位置附近往复的运动.这一振 动系统叫做单摆. 求单摆小角 度振动时的周期. l m o A 5

5-1简谐运动简谐运动的振幅周期频率和相位 物理学教程 (第二版) 解0<5°时,sin0≈0 转动 正向 M=-nglsin0≈-mgl0 d20 -mgl0 =J dr2 d20 =-80 dt2 令02=8 d20 dt2 =-020 0=0 cos(a+o) T=2元 l/g J=ml2 第五章机械振动
物理学教程 (第二版) 第五章 机械振动 5 – 1 简谐运动 简谐运动的振幅 周期 频率和相位 l m o A M = −mglsin −mgl 2 2 d d t mgl J − = 2 J = ml l g t = − 2 2 d d 2 2 2 d d = − t cos( ) = m t + l g = 2 令 FT P T = 2π l g 转动 正向 5 ,sin 解 时