-6电势 9 物理学教程 第二版) 静电场的环路定理 fE.di-o 电势 电场的电势(势函数) 静电场的保守性意味着,对静 电场来说,存在着一个由电场 中各点位置决定的标量函数 ∫AB9oE·d=-(Epe-Ena E ∫nEdl=-( pB E 9o 9o 此积分大小与9无关,仅与A、B位置有关, 第九章静电场
第九章 静电场 物理学教程 9 - 6 电 势 (第二版) d = 0 l E l ➢ 静电场的环路定理 ➢ 电场的电势(势函数): 静电场的保守性意味着,对静 电场来说,存在着一个由电场 中各点位置决定的标量函数. E q0 A B 一 电势 d ( ) 0 p 0 p q E q E E l B A A B = − − 此积分大小与 q0 无关,仅与 A、B 位置有关. d ( ) 0 pB pA AB q E l = − E − E
9-6电势 物理学教程 (第二版) 此标量函数(电势)在A、B两点的数值之差等 于从A到B移动单位正电荷时静电场力所做的功, LE.d7= B 19o SpE.d7=-(VB-Va) B点电势V= A点电势 V,= 90 90 ,=J。E-d+(V为参考电势,值任选) 第九章静电场
第九章 静电场 物理学教程 9 - 6 电 势 (第二版) E q0 A B B AB VA = E l +V d d ( ) 0 p 0 p q E q E E l B A A B = − − 0 p q E V A A 点电势 A = 0 p q E V B B 点电势 B = ( 为参考电势,值任选) VB d ( ) B A AB E l = − V −V 此标量函数(电势)在A、B 两点的数值之差等 于从A到B移动单位正电荷时静电场力所做的功

9-6电势 物理学教程 (第二版) VI=JE.di+Vm V=0点 E.d7 令,=0y4=∫E.d A ◆电势零点选择方法:有限带电体以无穷远为电势 零点,实际问题中常选择地球电势为零. V.=SE.dl 物理意义把单位正试验电荷从点A移到无穷远 时,静电场力所作的功, 电势差 Ua=y-V。=JEd 第九章静电场
第九章 静电场 物理学教程 9 - 6 电 势 (第二版) B AB VA = E l +V d 令 = 0 VB = AB A V E l d 电势零点选择方法:有限带电体以无穷远为电势 零点,实际问题中常选择地球电势为零. = A A V E l d = − = AB AB A B U V V E l 电势差 d V E l V A A d 0 = = 点 物理意义 把单位正试验电荷从点 A 移到无穷远 时,静电场力所作的功

9-6电势 物理学教程 (第二版) 电势差 U4s=Va-V。=Edl AR (将单位正电荷从A移到B电场力作的功.) 并美骑差是绝对的,与电势零点的滋无关, 电势大小是相对的,与电势零点的选择有关 静电场力的功WAB=qo'4-q'B=-9UBA 单位:伏特(V) 原子物理中能量单位1eV=1.602×10-19J 第九章静电场
第九章 静电场 物理学教程 9 - 6 电 势 (第二版) (将单位正电荷从 A 移到 B 电场力作的功.) = − = AB AB A B U V V E l 电势差 d 电势差是绝对的,与电势零点的选择无关; 电势大小是相对的,与电势零点的选择有关. 注意 AB A B UBA W q V q V q 静电场力的功 = 0 − 0 = − 0 1eV 1.602 10 J −19 原子物理中能量单位 = 单位:伏特 (V)

9-6电势 物理学教程 (第二版) 二 点电荷的电势 E 令V=0 grdr 4π6r3 9 f9>0,V>0 4元Eor 1g<0,V<0 第九章静电场
第九章 静电场 物理学教程 9 - 6 电 势 (第二版) q r l d E 二 点电荷的电势 r r q E 3 4π 0 = 令 V = 0 = r r l r q V d 4π 3 0 r q V 4π 0 = dr 0, 0 0, 0 q V q V = r r qr r 3 4π 0 d

9-6电势 物理学教程 (第二版) 三 电势的叠加原理 ◆点电荷系E=∑E, 9 V=jE.dl=∑jE,d 92 A 93 ,-Σ. dq 电荷连续分布 dE Vx= dq 4元8or 第九章静电场
第九章 静电场 物理学教程 9 - 6 电 势 (第二版) 1 q 2 q 3 q 三 电势的叠加原理 点电荷系 = i E Ei = A A V E l d E l i A i = d = = i i i i A Ai r q V V 0 4π 电荷连续分布 = r q VP 4π 0 d A 1 r E1 2 r 3 r E2 E3 + + + + ++ + + + + ++ + ++ + q E d r P dq = dV dq +

9-6电势 物理学教程 (第二版) >利用 dq 讨论 4元8or (利用了点电荷电势V=g/4兀o, 求电势 这一结果已选无限远处为电势零点,即使 的方法 用此公式的前提条件为有限大带电体且选 无限远处为电势零点.) > 若已知在积分路径上E的函数表达式, 则 V=0点 V4= E.di 第九章静电场
第九章 静电场 物理学教程 9 - 6 电 势 (第二版) 求电势 的方法 = r q VP 4π 0 d ➢ 利用 ➢ 若已知在积分路径上 的函数表达式, 则 E V E l V A A d 0 = = 点 (利用了点电荷电势 , 这一结果已选无限远处为电势零点,即使 用此公式的前提条件为有限大带电体且选 无限远处为电势零点.) V q r 4π 0 = / 讨论
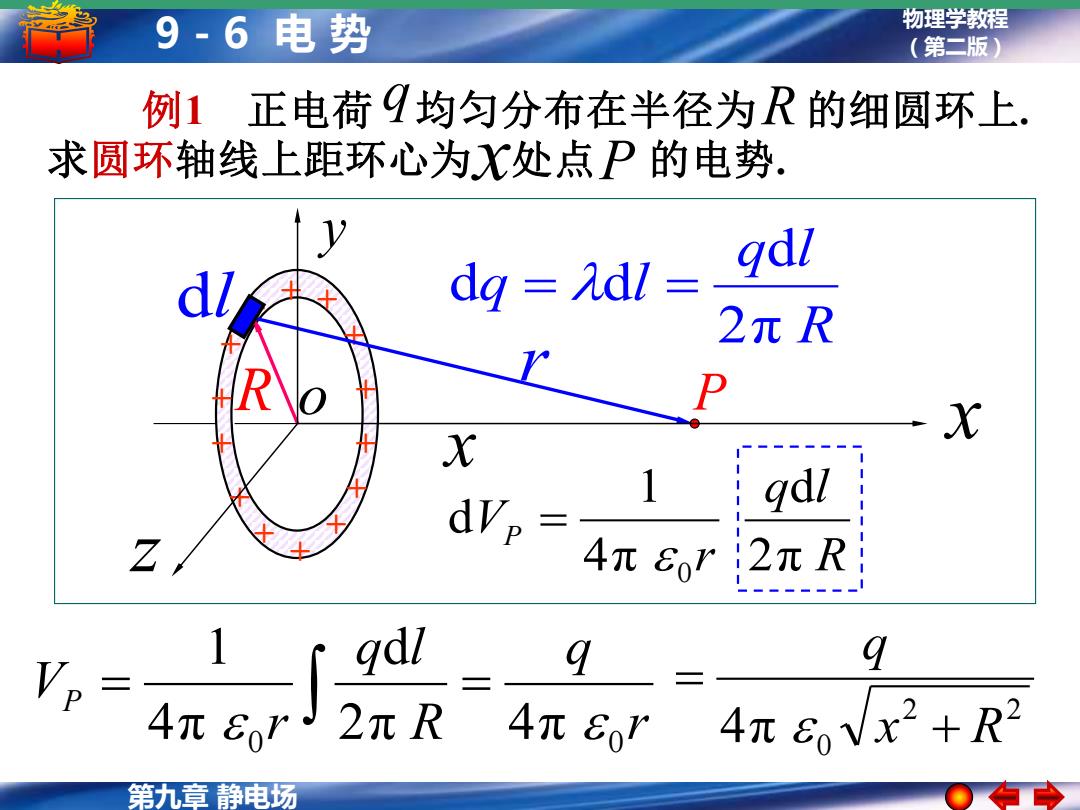
9-6电势 物理学教程 (第二版) 例1正电荷9均匀分布在半径为R的细圆环上. 求圆环轴线上距环心为X处点P的电势. 17 gdl dg Adl = 2元R P X X 1 dVp qdl Z 4π6r2πR 9dl 9 9 4π6rJ 2元R 4元8or 4π6Vx2+R2 第九章静电场
第九章 静电场 物理学教程 9 - 6 电 势 (第二版) R q l r VP 2π d 4π 1 d 0 = r q R q l r VP 0 2π 4π 0 d 4π 1 = = 2 2 4π 0 x R q + = + + + + + + + + + + + + + + R r 例1 正电荷 均匀分布在半径为 的细圆环上. 求圆环轴线上距环心为 处点 的电势. q R x P dl x P R q l q l 2π d d = d = o y z x
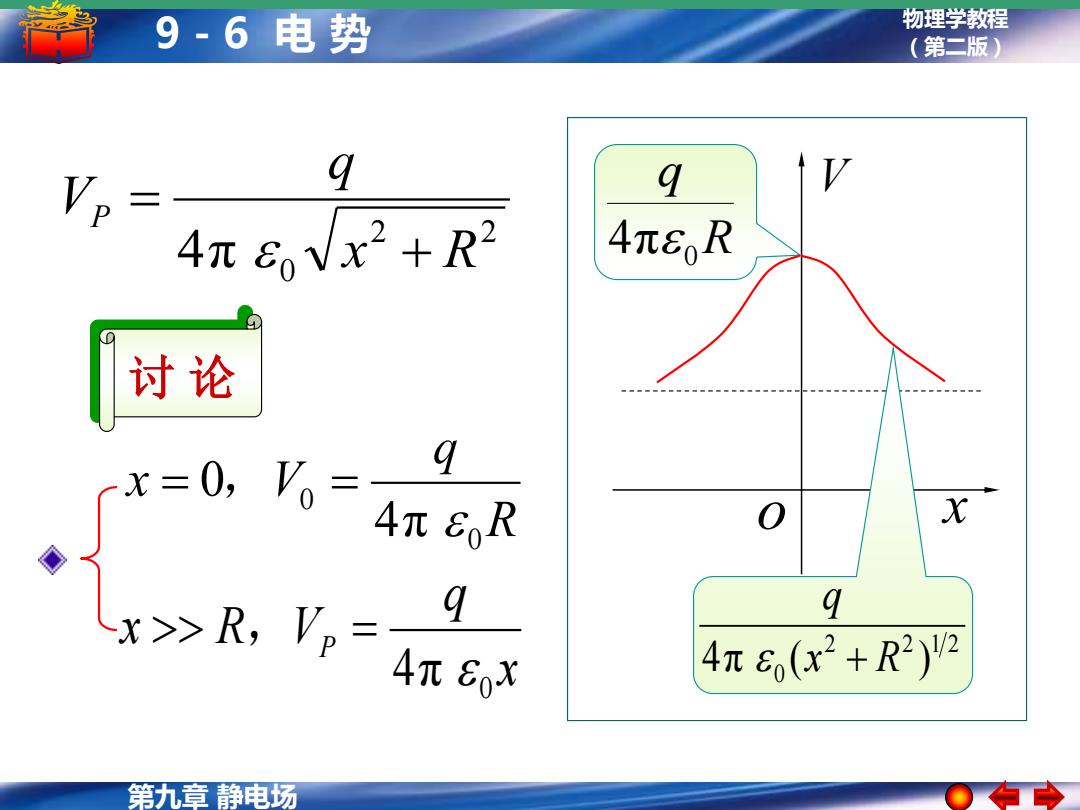
9-6电势 物理学教程 (第二版) q 4元6,Vx2+R 4π6R 讨论 x=0,V= 9 4π6R xR,Vn=AT 6o q 9 4π6(x2+R2)'2 第九章静电场
第九章 静电场 物理学教程 9 - 6 电 势 (第二版) R q x V 0 0 4π 0 = , = x q x R VP 0 4π , = 2 2 4π 0 x R q VP + = 讨 论 R q 4π 0 o x V 2 2 1 2 0 4π (x R ) q +

9-6电势 物理学教程 (第二版) 均匀带电薄圆盘轴线上的电势 dg=o2πrd x2+r2 X X RG2元rdr VP-7 O π60Vx2+r2 (Nx2+R2-x) 260 x>>RVx2+R2≈x+ R2 V≈2/4π6x 2x (点电荷电势) 第九章静电场
第九章 静电场 物理学教程 9 - 6 电 势 (第二版) R o x ( ) 2 2 2 0 = x + R − x 2 2 x + r x P dq = 2π rdr r dr + = R P x r r r V 0 2 2 0 2π d 4π 1 x R x R x R x 2 2 2 2 + + V Q x 4π 0 (点电荷电势) 均匀带电薄圆盘轴线上的电势