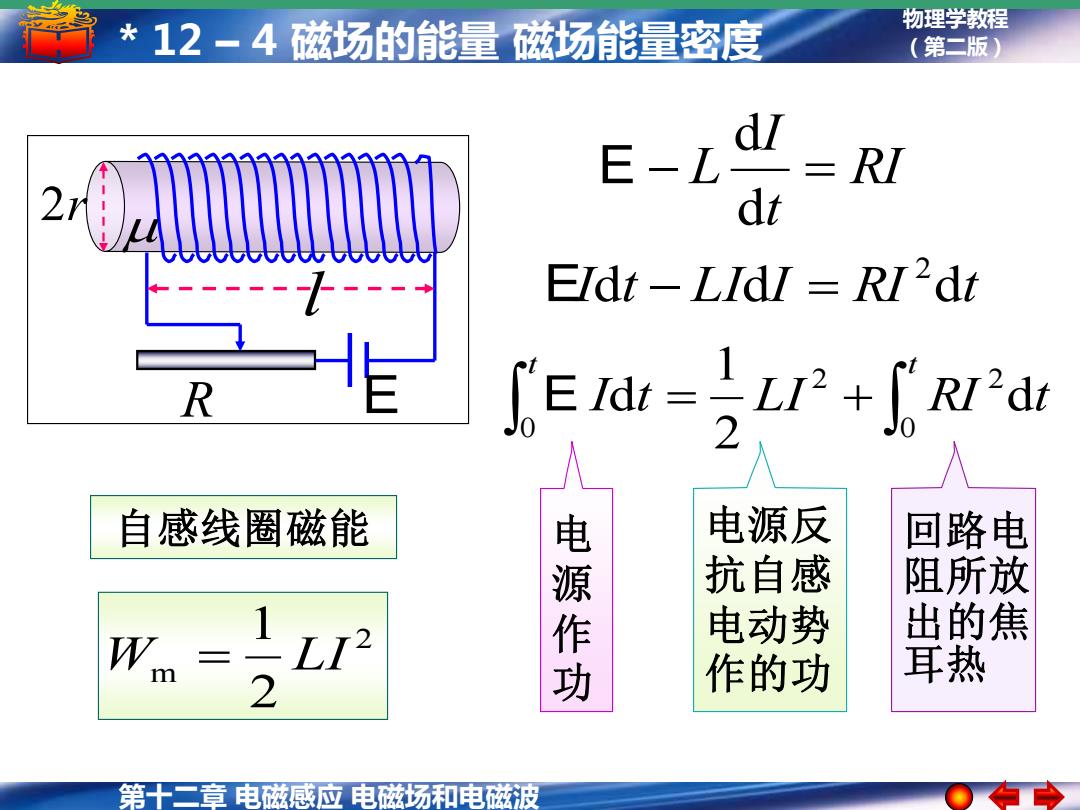
*12-4磁场的能量磁场能量密度 物理学教程 (第二版) dl E-L =RI dt Eldt-LIdl RI'dt =L+RI'd 2 自感线圈磁能 电源反 回路电 抗自感 阻所放 Wm L 源作 电动势 出的焦 2 作的功 耳热 第十二章电磁感应电磁场和电磁波
第十二章 电磁感应 电磁场和电磁波 物理学教程 * 12 – 4 磁场的能量 磁场能量密度 (第二版) 自感线圈磁能 2 m 2 1 W = LI 回路电 阻所放 出的焦 耳热 RI t I − L = d d E = + t t I t LI RI t 0 2 2 0 d 2 1 E d Idt LIdI RI dt 2 E − = 电 源 作 功 电源反 抗自感 电动势 作的功 l 2r R E

*12-4磁场的能量磁场能量密度 物理学教程 (第二版) ◆ 自感线圈磁能 Wm三 LI2 L=un2V,B=unl g=-m(2-} V=wmV Ln 2 u ◆磁场能量密度 Wm B 2= 2 ◆磁场能量 形-dv-ga 2u 第十一章电磁感应电滋场和电磁波
第十二章 电磁感应 电磁场和电磁波 物理学教程 * 12 – 4 磁场的能量 磁场能量密度 (第二版) L = n V , B = nI 2 2 2 2 m ( ) 2 1 2 1 n B W LI n V = = V B 2 2 1 = = wm V 磁场能量密度 H BH B w 2 1 2 1 2 2 2 m = = = 磁场能量 = = V V V B W w V d 2 d 2 m m 自感线圈磁能 2 m 2 1 W = LI I L

*12-4磁场的能量磁场能量密度 物理学教程 (第二版) 例1有一长为l=0.20m、截面积S=5.0cm的长 直螺线管.按设计要求。当螺线管通以电流I=450mA 时,螺线管可储存磁场能量W,=0.10J.试问此长直螺 线管需绕多少匝线圈? 解由上一节可知,长直螺线管的自感为 L=4N2S/1 螺线管储存的磁场能量为 2 N= 第十二章电磁感应电磁场和电磁波
第十二章 电磁感应 电磁场和电磁波 物理学教程 * 12 – 4 磁场的能量 磁场能量密度 (第二版) 例1 有一长为 、截面积 的长 直螺线管. 按设计要求。当螺线管通以电流 时,螺线管可储存磁场能量 . 试问此长直螺 线管需绕多少匝线圈? l = 0.20m 2 S = 5.0cm I = 450mA m W = 0.10J 解 由上一节可知,长直螺线管的自感为 2 0 L N S l = / 螺线管储存的磁场能量为 2 2 2 0 m 1 1 2 2 N S W LI I l = = m 1/ 2 0 1 2 ( ) W l N I S = 4 = 1.8 10 匝
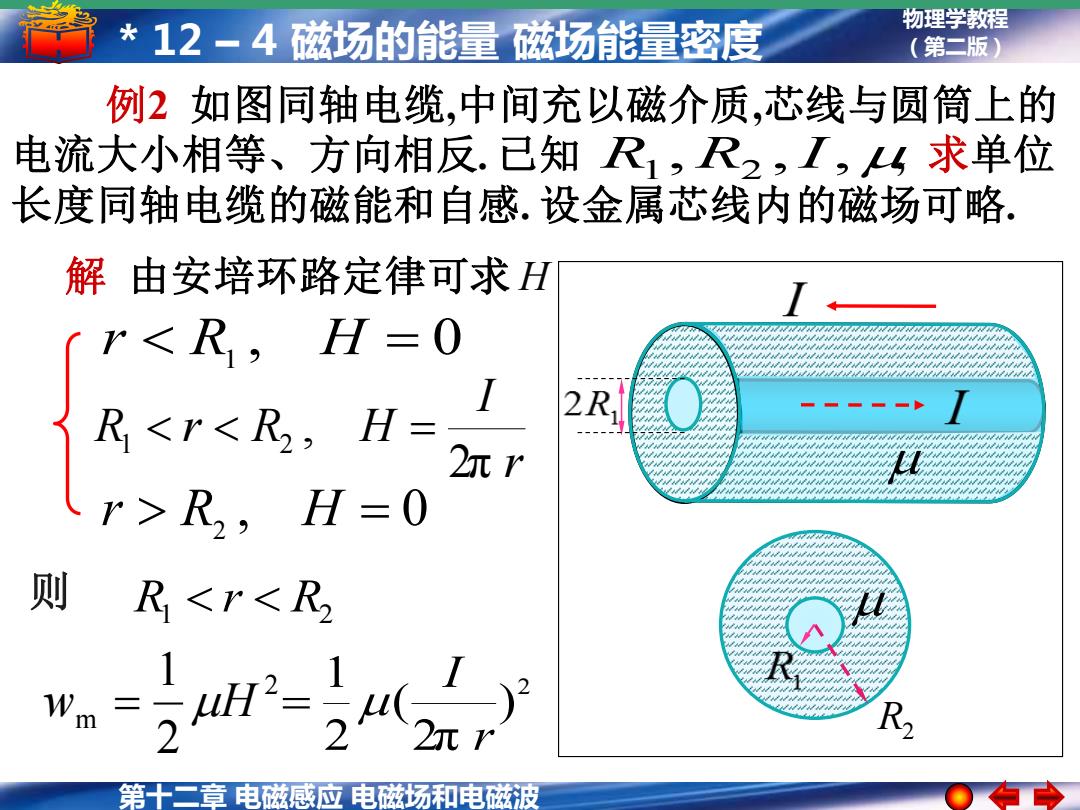
*12-4磁场的能量磁场能量密度 物理学教程 (第二版) 例2如图同轴电缆,中间充以磁介质,芯线与圆筒上的 电流大小相等、方向相反.已知R1,R2,I,;求单位 长度同轴电缆的磁能和自感.设金属芯线内的磁场可略. 解由安培环路定律可求H R,,H=0 则 R<r<R 2-243 电磁感应电滋场和电磁玻
第十二章 电磁感应 电磁场和电磁波 物理学教程 * 12 – 4 磁场的能量 磁场能量密度 (第二版) 例2 如图同轴电缆,中间充以磁介质,芯线与圆筒上的 电流大小相等、方向相反. 已知 , 求单位 长度同轴电缆的磁能和自感. 设金属芯线内的磁场可略. R1 ,R2 ,I, 解 由安培环路定律可求 H r I R r R H 2π , 1 2 = r R1 , H = 0 r R2 , H = 0 2 m 2 1 w = H 2 ) 2π ( 2 1 r I = 则 1 R2 R r R2
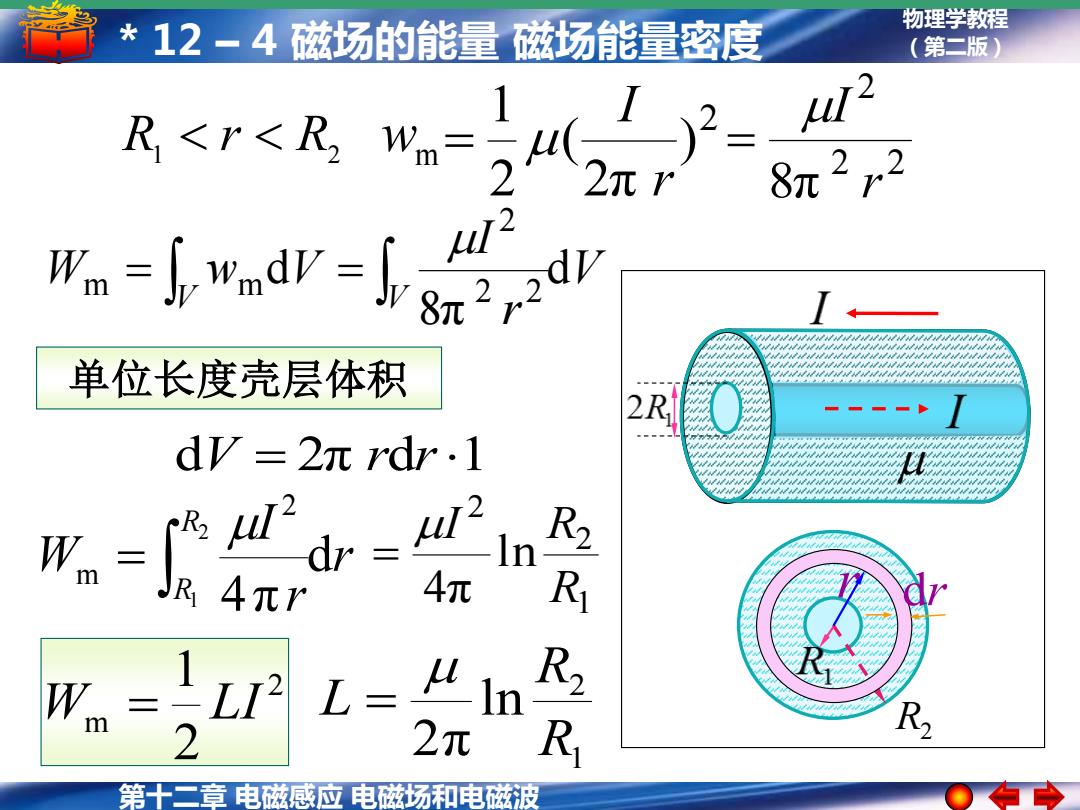
*12-4磁场的能量磁场能量密度 物理学教程 (第二版) 22 8元 所-r- 单位长度壳层体积 2R dV=2πrdr.1 _dr u 4元r 4元 R w。=L12 L= R2 2元 R 第十二章电磁感应电磁场和电磁波
第十二章 电磁感应 电磁场和电磁波 物理学教程 * 12 – 4 磁场的能量 磁场能量密度 (第二版) wm 2 ) 2π ( 2 1 r I = 2 2 2 8π r I R1 r R2 = V r I W w V V V d 8π d 2 2 2 m m = = R2 r dr 单位长度壳层体积 dV = 2π rdr1 r r I W R R d 4π 2 1 2 m = 1 2 2 ln 4π R I R = 2 m 2 1 W = LI 1 2 ln 2π R R L =