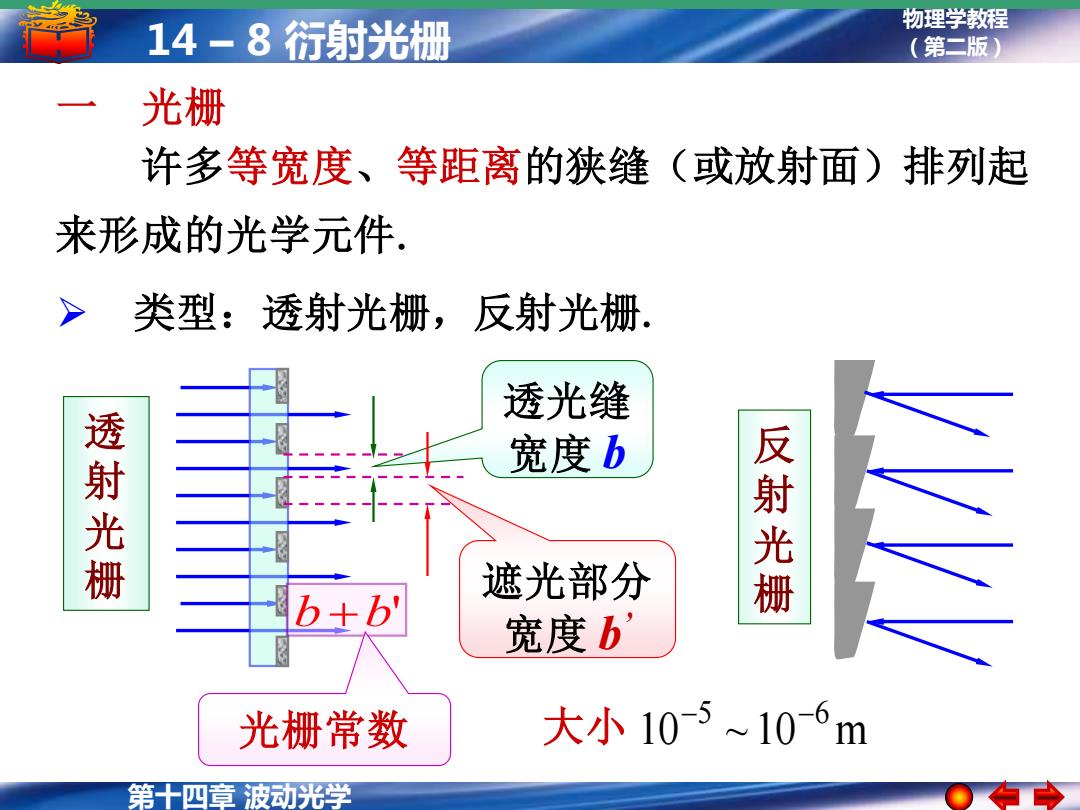
14-8衍射光栅 物理学教程 (第二版) 光栅 许多等宽度、等距离的狭缝(或放射面)排列起 来形成的光学元件. 类型:透射光栅,反射光栅 透光缝 透射光栅 宽度b 遮光部分 反射光栅 b+b 宽度b 光栅常数 大小10-5≈10-6m 第十四章波动光学
第十四章 波动光学 物理学教程 14 – 8 衍射光栅 (第二版) 一 光栅 许多等宽度、等距离的狭缝(或放射面)排列起 来形成的光学元件. ➢ 类型:透射光栅,反射光栅. 反 射 光 栅 透 射 光 栅 透光缝 宽度 b 遮光部分 宽度 b ’ b+b' 光栅常数 10 ~ 10 m 大小 −5 −6
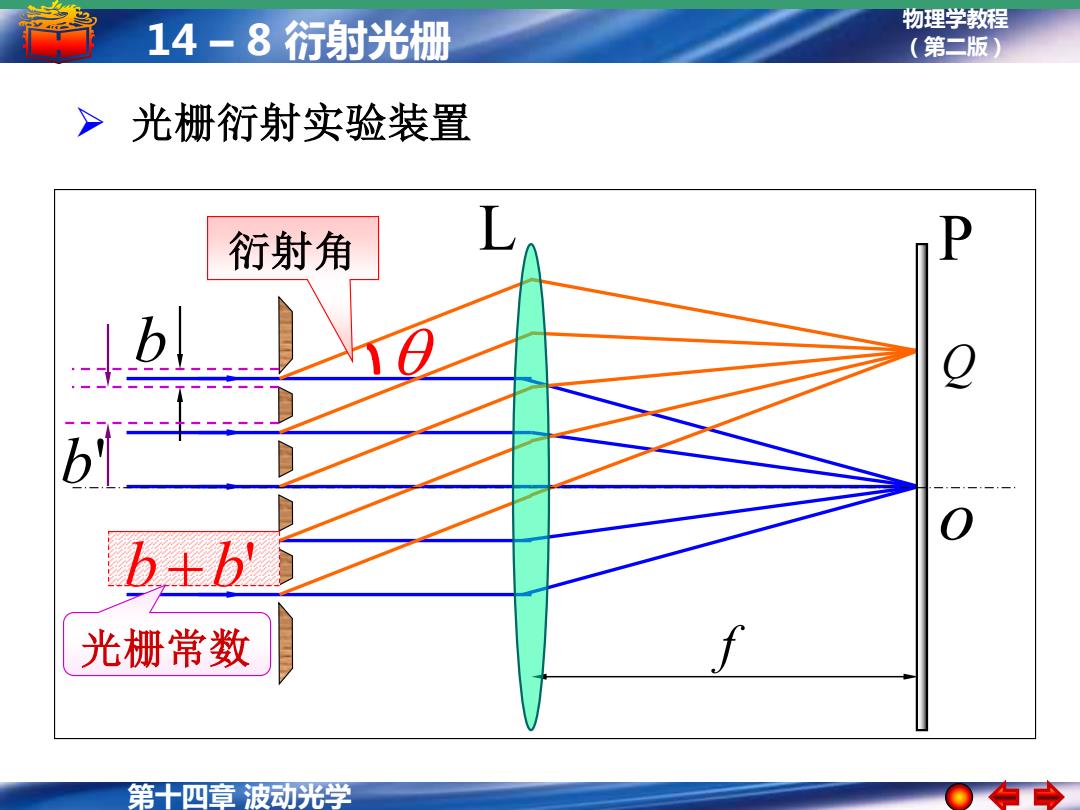
14-8衍射光栅 物理学教程 (第二版) >光栅衍射实验装置 衍射角 b! b土b 光栅常数 第十四章波动光学
第十四章 波动光学 物理学教程 14 – 8 衍射光栅 (第二版) Q o L P f 衍射角 b b' b +b' 光栅常数 ➢ 光栅衍射实验装置
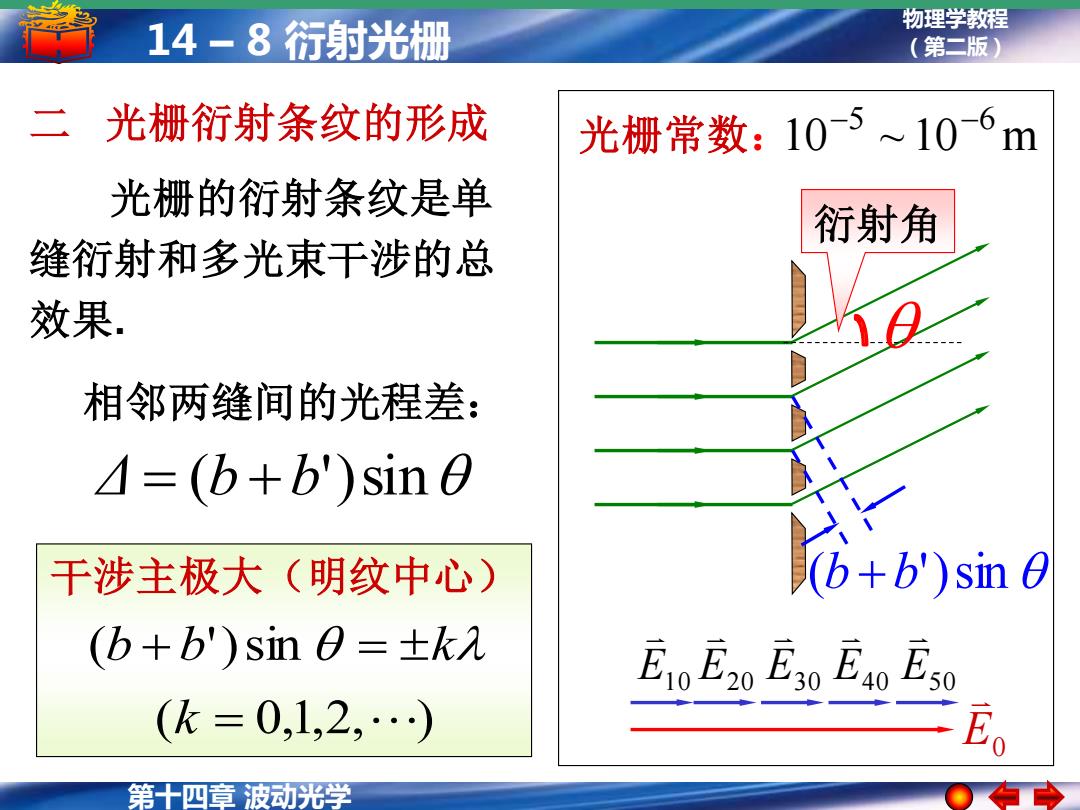
14-8衍射光栅 物理学教程 (第二版) 二 光栅衍射条纹的形成 光栅常数:105~10-6m 光栅的衍射条纹是单 衍射角 缝衍射和多光束干涉的总 效果. 相邻两缝间的光程差: =(b+b')sin0 干涉主极大(明纹中心) (b+b')sin 0 (b+b')sin0=±kλ (k=0,1,2,…) E 第十四章波动光学
第十四章 波动光学 物理学教程 14 – 8 衍射光栅 (第二版) 光栅常数: 10 ~ 10 m −5 −6 衍射角 ( 0,1,2, ) ( ')sin = + = k b b k 干涉主极大(明纹中心) 相邻两缝间的光程差: Δ = (b + b')sin (b +b')sin 二 光栅衍射条纹的形成 光栅的衍射条纹是单 缝衍射和多光束干涉的总 效果. E10 E20 E30 E40 E50 E0
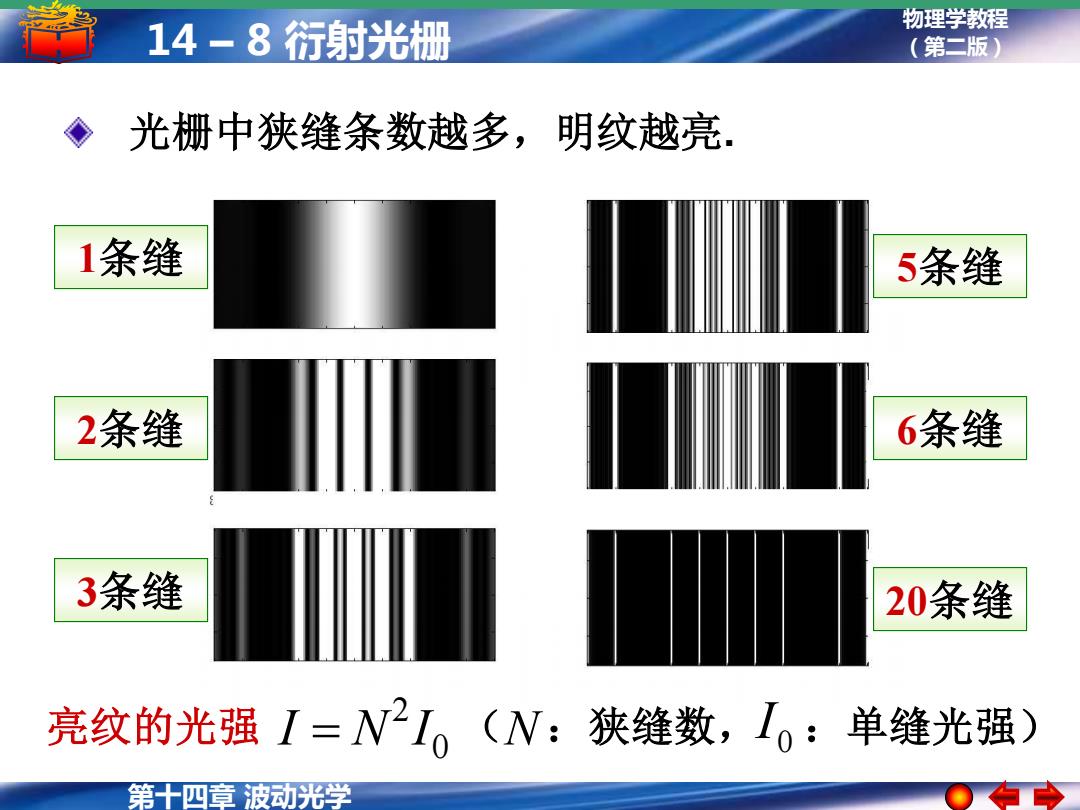
14-8衍射光栅 物理学教程 (第二版) 光栅中狭缝条数越多,明纹越亮, 1条缝 5条缝 2条缝 6条缝 3条缝 20条缝 亮纹的光强I=N2I,(W:狭缝数,I0:单缝光强) 第十四章波动光学
第十四章 波动光学 物理学教程 14 – 8 衍射光栅 (第二版) 光栅中狭缝条数越多,明纹越亮. 1条缝 2条缝 3条缝 5条缝 6条缝 20条缝 亮纹的光强 0 2 I = N I (N :狭缝数,I 0 :单缝光强)
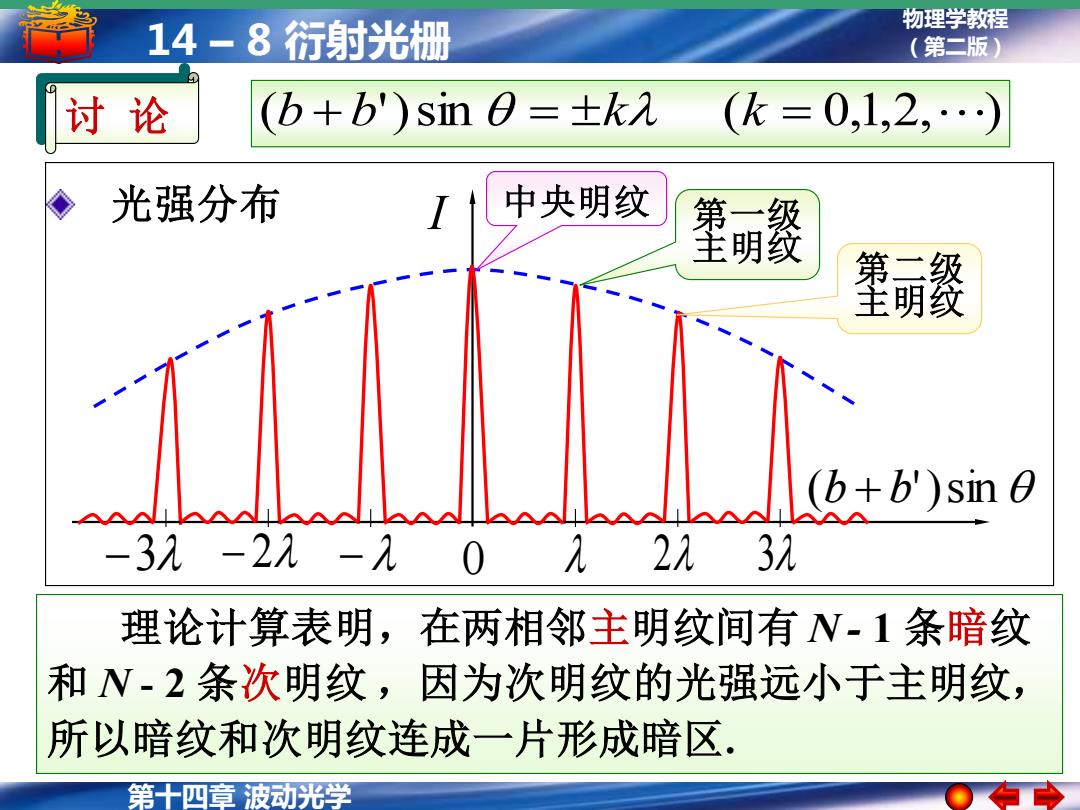
14-8衍射光栅 物理学教程 (第二版) 讨论 (b+b')sin0=±k2 (k=0,1,2,…) 光强分布 中央明纹 望明援 望餐 (b+b')sin O -32-22-0232 理论计算表明,在两相邻主明纹间有N-1条暗纹 和N-2条次明纹,因为次明纹的光强远小于主明纹, 所以暗纹和次明纹连成一片形成暗区. 第十四章波动光学
第十四章 波动光学 物理学教程 14 – 8 衍射光栅 (第二版) 讨 论 (b + b')sin = k (k = 0,1,2, ) (b + b')sin −3 − 2 − 0 2 3 光强分布 I 中央明纹 第一级 主明纹 第二级 主明纹 理论计算表明,在两相邻主明纹间有 N - 1 条暗纹 和 N - 2 条次明纹 ,因为次明纹的光强远小于主明纹, 所以暗纹和次明纹连成一片形成暗区

14-8衍射光栅 物理学教程 (第二版) 讨论 (b+b)sin0=±k入 (k=0,1,2,) 条纹最高级数 k见 sin8k=± b+b 0= b+b 2 k=kmax= △k=1,sin0k+l-sin8k= b+b ◆ 光栅常数越小,明纹越窄,明纹间相隔越远 元一定,b+b'减少,01一0增大. ◆入射光波长越大,明纹间相隔越远 b+b一定,九增大,01-0增大. 第十四章波动光学
第十四章 波动光学 物理学教程 14 – 8 衍射光栅 (第二版) ' 1, sin 1 sin b b k k k + = + − = 一定, b+b' 减少, k+1 − k 增大. ' b + b 一定, 增大, k+1 − k 增大. 光栅常数越小,明纹越窄,明纹间相隔越远 入射光波长越大,明纹间相隔越远 ' sin b b k k + = ' , 2 π max b b k k + = = = 条纹最高级数 讨 论 (b + b')sin = k (k = 0,1,2, )

14-8衍射光栅 物理学教程 (第二版) 单缝衍射对光栅衍射的影响(缺级现象) >单缝衍射 干涉相消(暗纹) bsin0=±2k 2 干涉加强(明纹) 2sin0=±(2k+) >多缝干涉极大 (b+b')sin0=±kλ (k=0,1,2,…) 第十四章波动光学
第十四章 波动光学 物理学教程 14 – 8 衍射光栅 (第二版) 2 sin 2 b = k 干涉相消(暗纹) 2 sin (2 1) b = k + 干涉加强(明纹) ➢ 单缝衍射 单缝衍射对光栅衍射的影响(缺级现象) (b + b')sin = k (k = 0,1,2, ) ➢ 多缝干涉极大
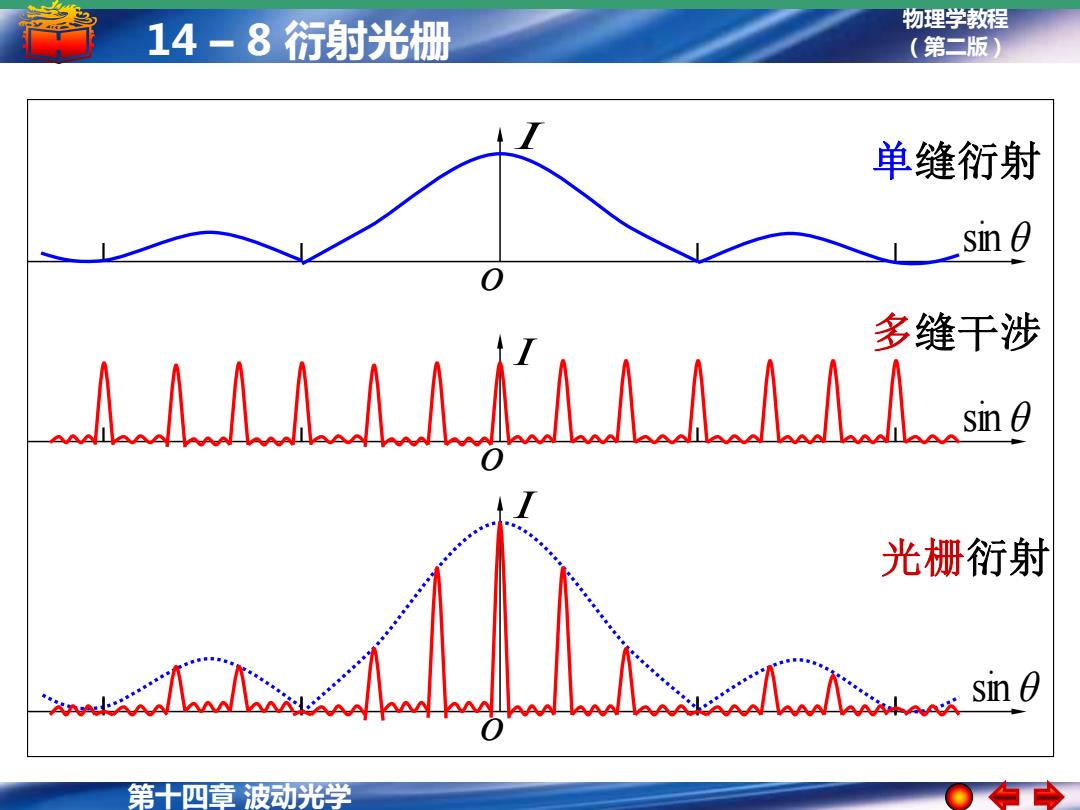
14-8衍射光栅 物理学教程 (第二版) 单缝衍射 snθ 多缝干涉 人人人人人LAAAAA人人m9 光栅衍射 第十四章波动光学
第十四章 波动光学 物理学教程 14 – 8 衍射光栅 (第二版) o sin I 单缝衍射 sin I o 多缝干涉 sin I o 光栅衍射
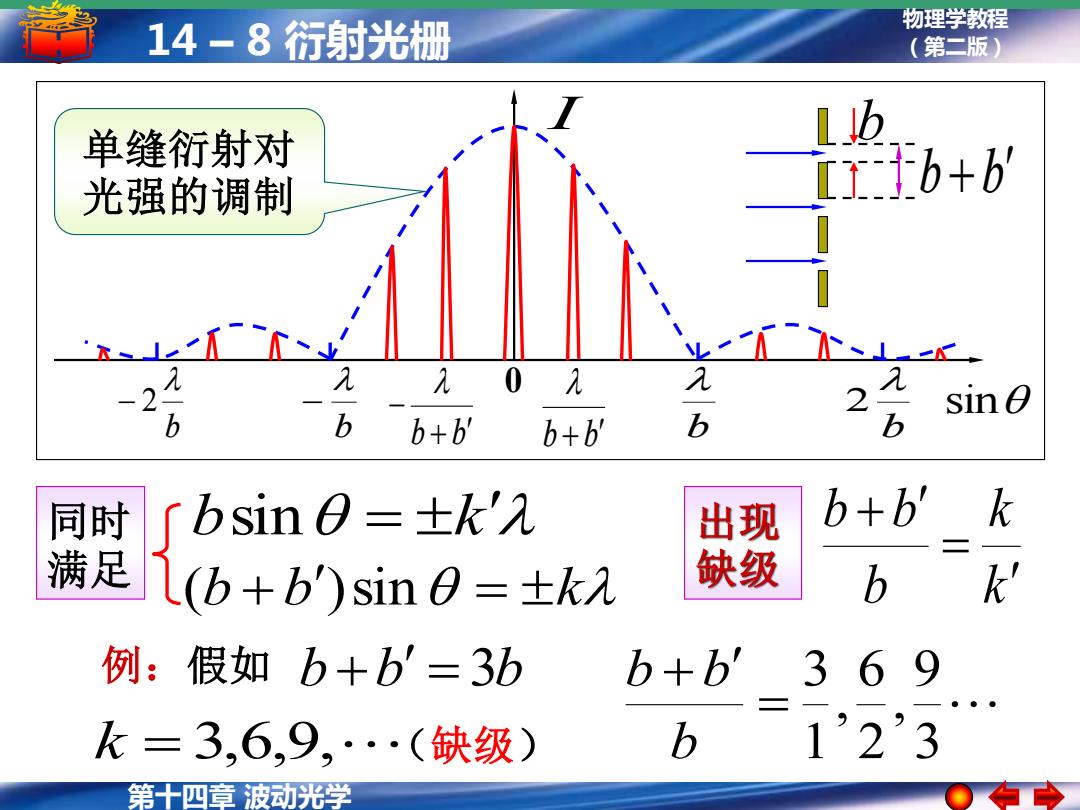
14-8衍射光栅 物理学教程 (第二版) 单缝衍射对 1 光强的调制 1Fb+6 xC 2 2 sin O b b+b b+b b 6 同时 [bsin0=±k'λ 出现 b+b' k 满足 l(b+b')sin0=±k2 缺级 b k' 例:假如b+b'=3b b+b'3 69 k=3,6,9,…(缺级) b 1’23 第十四章波动光学
第十四章 波动光学 物理学教程 14 – 8 衍射光栅 (第二版) 3 9 , 2 6 , 1 3 = + b b b k = 3,6,9, (缺级) 0 sin b b 2 b − b − 2 I b + b b + b − b b +b k k b b b = 出现 + 缺级 例:假如 b +b = 3b bsin = k (b + b)sin = k 同时 满足 单缝衍射对 光强的调制

14-8衍射光栅 物理学教程 (第二版) b+b' 3 b sin 9 b+b' b+b 765432101234567 缺 缺 缺 缺 第十四章波动光学
第十四章 波动光学 物理学教程 14 – 8 衍射光栅 (第二版) 缺 缺 缺 缺 7 6 5 4 3 2 1 0 1 2 3 4 5 6 7 0 sin b b 2 b − b − 2 I b + b b + b − 1 3 = + b b b