
物理学教程 10-4电容 (第二版) 电容器电容 电容器电容 C 2 VA-VB 单位 1F=1C/八V 1uF=10-6F 1pF=10-12F U=J E-d 电容的大小仅与导体的形状、相对位置、其间的 电介质有关.与所带电荷量无关 第十章静电场中的导体与电介质
第十章 静电场中的导体与电介质 物理学教程 10 – 4 电 容 (第二版) 一 电容器 电容 电容器电容 U Q V V Q C A B = − = 电容的大小仅与导体的形状、相对位置、其间的 电介质有关. 与所带电荷量无关. VB VA −Q + Q U E l AB AB = d 单位 1F =1C/V 1pF 10 F −12 = 1μF 10 F −6 =

10-4电容 物理学教程 (第二版) > 击穿场强E: 电容器中的电介质能承受的最大电 场强度 >击穿电压U:Eb= (平行板电容器) d >电容器电容的计算 步骤 1) 设两极板分别带电士Q; 2)求E; 3)求UU; 4)求C. 第十章静电场中的导体与电介质
第十章 静电场中的导体与电介质 物理学教程 10 – 4 电 容 (第二版) ➢ 电容器电容的计算 1)设两极板分别带电 ; 2)求 ; Q E 3)求 U ; 4)求 C . 步骤 ➢ 击穿场强 :电容器中的电介质能承受的最大电 场强度. Eb ➢ 击穿电压 Ub : 0 b U E d = (平行板电容器)

物理学教程 10-4电容 (第二版) 例1平板电容器.如图所示,平板电容器由两个彼 此靠得很近的平行极板A、B所组成,两极板的面积均 为S,两极板间距为山.极板间充满相对电容率为e的电 介质求此平板电容器的电容。 (1)设两导体板分别带电士Q (2)两带电平板间的电场强度 E=- Q EoE, EoES S (3)两带电平板间的电势差 U=Ed= Od So&S S (4)平板电容器电容 U d 第十章静电场中的导体与电介质
第十章 静电场中的导体与电介质 物理学教程 10 – 4 电 容 (第二版) d S A B + + + + + + Q −Q - - - - - - 0 r 0 r Q E S = = (2)两带电平板间的电场强度 (1)设两导体板分别带电 Q 0 r Qd U Ed S = = (3)两带电平板间的电势差 0 r Q S C U d = = (4)平板电容器电容 例1 平板电容器. 如图所示,平板电容器由两个彼 此靠得很近的平行极板A、B 所组成,两极板的面积均 为S,两极板间距为d. 极板间充满相对电容率为 的电 介质.求此平板电容器的电容. r

10-4电容 物理学教程 (第二版) 例2圆柱形电容器.如图所示,圆柱形电容器是由 半径分别为R和R,的两同轴圆柱面A和B所构成,且 圆柱体的长度1比半径R大的多.两圆柱面之间充以相对 电容率为£的电介质.求此圆柱形电容器的电容. 解:(1)设两导体圆柱面单位长度上 1>ZRB 分别带电土入 (2)E= Q 1 2元66r (3)U= Adr 人R2GG -In RB 第十章静电场中的导体与电介质
第十章 静电场中的导体与电介质 物理学教程 10 – 4 电 容 (第二版) 例2 圆柱形电容器. 如图所示,圆柱形电容器是由 半径分别为 和 的两同轴圆柱面A 和 B 所构成,且 圆柱体的长度 l 比半径 大的多. 两圆柱面之间充以相对 电容率为 的电介质. 求此圆柱形电容器的电容. RA RB RB r 0 r 0 r 1 2 π 2 π Q E r l r (2) = = (1)设两导体圆柱面单位长度上 分别带电 解: (3) A B 0 r 0 r ln 2π 2π R R l Q r dr U B A R R = = RA RB l B l R + + + + - - - -
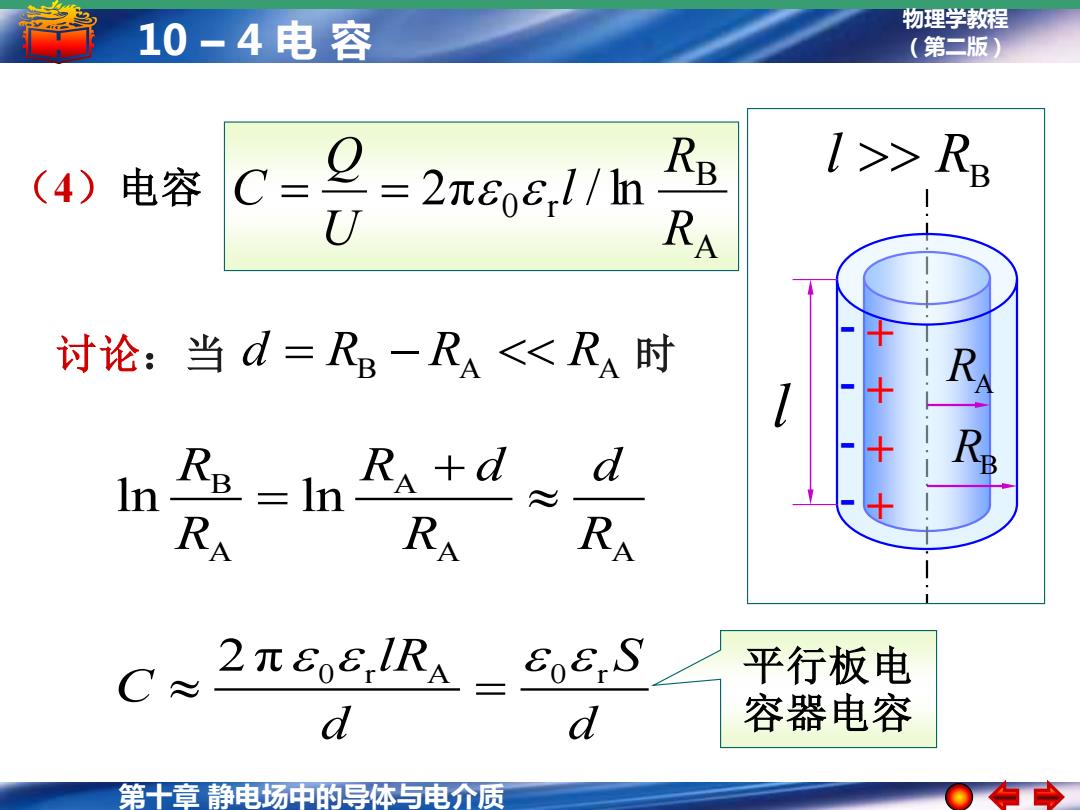
物理学教程 10-4电容 (第二版) (4)电容 C= = U 2πeoc-l/1h Re 1>R RA 讨论:当d=R-RA<RA时 d In RA+d RA RA RA C 2πEOEIRA= EoE.s 平行板电 d d 容器电容 第十章静电场中的导体与电介质
第十章 静电场中的导体与电介质 物理学教程 10 – 4 电 容 (第二版) 平行板电 容器电容 2 π 0 r A 0 r lR S C d d = (4)电容 讨论:当 d R R R = − B A A 时 B A A A A ln ln R R d d R R R + = RA RB l B l R + + + + - - - - A B 0 r 2π / ln R R l U Q C = =

10-4电容 物理学教程 (第二版) 例3 球形电容器.球形电容器是由半径分别为R 两同心金属球壳所组成,两球壳间充垓相对电容 率为解的横正电(+Q) 外球带负电(-Q) (R<P<R2) = Q9 u=l8i40 R dr 第十章静电场中的导体与电介质
第十章 静电场中的导体与电介质 物理学教程 10 – 4 电 容 (第二版) R1 R2 + + + + + + + + − − − − − − − − r 2 r 0 r 4 π Q E e r = ( ) 1 R2 R r 2 1 2 0 r d d 4 π R l R Q r U E l r = = 0 r 1 2 1 1 ( ) 4 π Q R R = −P * 例 3 球形电容器. 球形电容器是由半径分别为 和 的两同心金属球壳所组成,两球壳间充以相对电容 率为 的电介质. R1 R2 r 外球带负电( ) 解 设内球带正电( + Q ) − Q
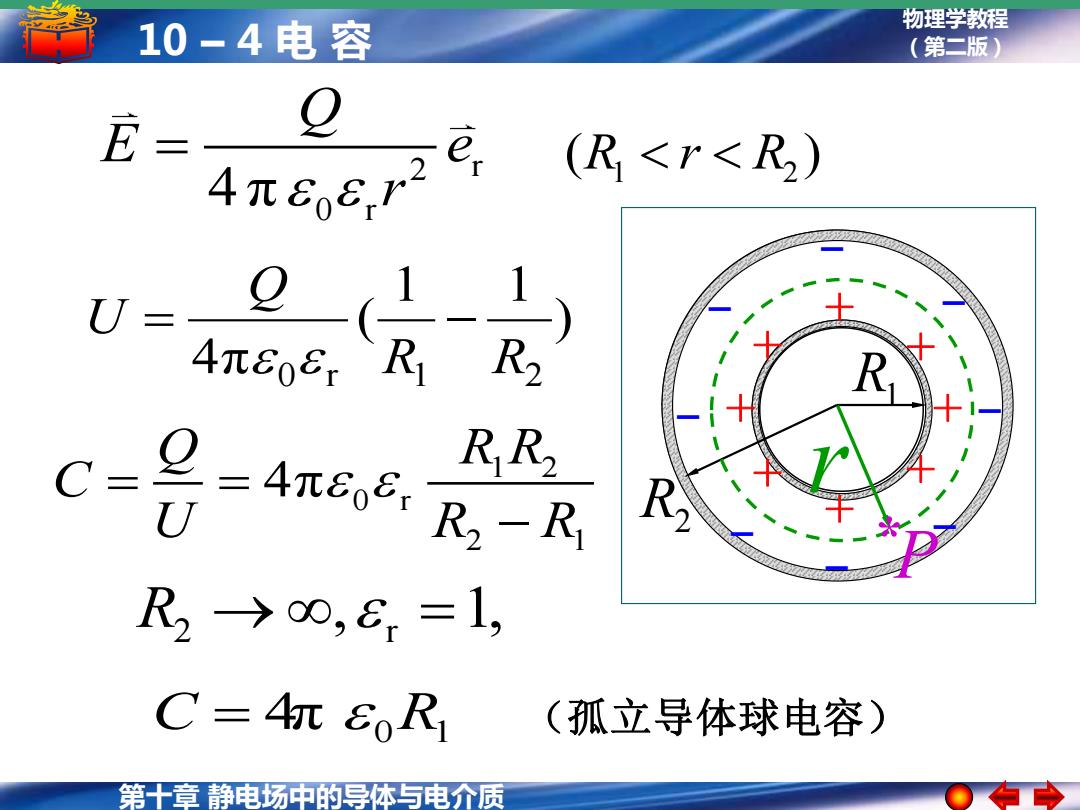
物理学教程 10-4电容 (第二版) 龙= 4元8o8r1 (R00,6=1, C=4n 8oR (孤立导体球电容) 第十章静电场中的导体与电介质
第十章 静电场中的导体与电介质 物理学教程 10 – 4 电 容 (第二版) 2 r 4 π 0 r Q E e r = ( ) 1 R2 R r 2 r R → = , 1, R1 R2 + + + + + + + + − − − − − − − − r P * 1 2 0 r 2 1 4π Q R R C U R R = = − C = 4π 0 R1 (孤立导体球电容) ) 1 1 ( 4π 0 r R1 R2 Q U = −

10-4电容 物理学教程 (第二版) 例4两球形电极间的击穿电压.为了防止两极间的 空气被击穿,通常避免采用尖端电极,而采用球形电极 然而,若两球形电极间存在高电压的情况下,球形电极 间的空气也会被击穿而放电.如图所示,由两个半径均 为r=2cm的球形电极放在击穿场强E,=30kV·cm 的空气中,两球的中心距为 D d=10cm.试粗略估算在上 述条件下,两球形电极间的 击穿电压大约是多少? 第十章静电场中的导体与电介质
第十章 静电场中的导体与电介质 物理学教程 10 – 4 电 容 (第二版) 例4 两球形电极间的击穿电压. 为了防止两极间的 空气被击穿,通常避免采用尖端电极,而采用球形电极. 然而,若两球形电极间存在高电压的情况下,球形电极 间的空气也会被击穿而放电. 如图所示,由两个半径均 为 r = 2cm 的球形电极放在击穿场强 的空气中,两球的中心距为 d = 10cm. 试粗略估算在上 述条件下,两球形电极间的 击穿电压大约是多少? 1 b E 30kV cm− = A B + + + + - - - - r d

物理学教程 10-4电容 (第二版) 例4两球形电极间的击穿电压, 已知:半径为r=2cm的球形电极 A B 击穿场强E。=30kV.cm 两球的中心距为d=10cm. 求:两球形电极间的击穿电压 解设球形电极A和B各有+Q和-Q的电荷, 忽略电极间的静电感应导致的电荷重新分布,且把 球形电极表面上的电荷视为集中于球心.则可得: 电极A表面的电势为 U4= 4元60 d 第十章静电场中的导体与电介质
第十章 静电场中的导体与电介质 物理学教程 10 – 4 电 容 (第二版) 例4 两球形电极间的击穿电压. 已知:半径为r = 2cm 的球形电极 击穿场强 两球的中心距为 d = 10cm. 求:两球形电极间的击穿电压 1 b E 30kV cm− = A B + + + + - - - - r d 解 设球形电极 A 和 B 各有 + Q 和 – Q 的电荷, 忽略电极间的静电感应导致的电荷重新分布,且把 球形电极表面上的电荷视为集中于球心. 则可得: 0 1 ( ) 4π A Q Q U r d r = − − 电极A表面的电势为

10-4电容 物理学教程 (第二版) 电极A表面的电势为 UA 4元80 1 电极B表面的电势为 UB= 4元60 两极间的电势差为 UAB= 2元80 d 球形电极表面附近处的电场强度为 B 。48gn 击穿场强E。=E,,此时U。=U4B 可得6-2a*7d =84.7kV 第十章静电场中的导体与电介质
第十章 静电场中的导体与电介质 物理学教程 10 – 4 电 容 (第二版) 0 1 ( ) 4π B Q Q U r d r − = + − 电极B表面的电势为 两极间的电势差为 0 1 1 ( ) 2π AB Q U r d r = − − 0 1 ( ) 4π A Q Q U r d r = − − 电极A表面的电势为 球形电极表面附近处的电场强度为 s 2 2 0 1 1 [ ] 4π ( ) Q E r d r = + − 击穿场强 E E b s = ,此时 U U b = AB A B + + + + - - - - r d ) 84.7kV ( ) 1 1 ) ( 1 1 2 ( 2 2 = − + − = − r d r r d r 可得 Ub Eb